Delta mi!

Narysujemy teraz figurę bardziej skomplikowaną: dwudziestościan...

W wielu rysunkach bardzo pomocny jest sześcian, z narysowaniem którego raczej nie mamy problemu...

Kontynuujemy opowieść o czworościanach równościennych – tym razem przyjrzymy się paru zadaniom z nimi związanym. Jakiś czas temu na konkursach matematycznych temat tych wdzięcznych czworościanów był dosyć modny...

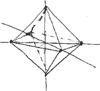
Kontynuujemy lekcje rysunku rozpoczęte w Delcie 6/2012. Kolejnym obiektem, który będziemy rysować, jest ośmiościan.

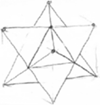
Wydaje się, że w czasach szybkich komputerów, programów graficznych i innych gadżetów nie ma sensu zajmowanie się rysunkiem odręcznym. Równie dobrze jednak można by zrezygnować z nauki pisania i tabliczki mnożenia – są przecież odpowiednie edytory i kalkulatory. Zdarza się jednak, że rozwiązując jakieś zadanie, dobrze byłoby podeprzeć naszą wyobraźnię właśnie rysunkiem, a nie ma pod ręką supernowoczesnych narzędzi.

W zawodach I stopnia obecnej, LXIII Olimpiady Matematycznej wzięło udział 1409 uczniów, więc nieco mniej niż w poprzedniej. Jest to liczba bliska wieloletniej średniej. Do drugiego stopnia zakwalifikowano 622 uczniów. Zawody drugiego stopnia odbyły się 17 i 18 lutego.

Czy istnieje czworościan który nie jest foremny, a którego ściany są trójkątami przystającymi? Istnieje...

Na płaszczyźnie, jeśli trójkąt ma równe boki, to jest równoboczny. W przestrzeni jednak czworościan, którego ściany są przystające, wcale nie musi być foremny...

Czasem przydaje się do czegoś twierdzenie o dwusiecznej...

Każdy, kto był w dżungli lub chociaż widział ją w jakimś filmie, wie, że poruszanie się po niej jest, delikatnie mówiąc, dosyć uciążliwe. Stanowi to ogromny kłopot szczególnie wtedy, gdy ktoś się w niej zgubi i chce się jakoś wydostać. Nie dość, że nie wiadomo, w jakim kierunku iść, to w ogóle ciężko jest nam pokonywać przeszkody (a rozwiązania siłowe, takie jak maczeta, niewiele dają). Istnieje następujące zalecenie: wystarczy znaleźć strumień (co zresztą wcale nie musi być łatwe), a potem liczyć na to, że zaprowadzi nas on do większej rzeki, a ta, być może, do morza.

W tym kąciku zajmiemy się pewnym zadaniem o czworościanie foremnym, o którym, między innymi, miałem okazję opowiadać na XLVI Szkole Matematyki Poglądowej pod hasłem Podejście niestandardowe.

Święta za pasem, więc przygotujmy się nieco do wieszania bombek na choince.

W tym odcinku przyjrzymy się kątom dwuściennym. Jedną z najbardziej skutecznych metod radzenia sobie z nimi jest przeformułowanie problemu tak, żeby zamiast kątów dwuściennych pojawiły się kąty płaskie.

Na pierwszym etapie tegorocznej Olimpiady Matematycznej pojawiło się poniższe zadanie 1 o numerowaniu krawędzi dwunastościanu. Spośród licznych zadań o podobnej tematyce prezentujemy kilka o dość różnorodnych rozwiązaniach.

W dniu 8 stycznia 2011 roku odbyły się zawody II stopnia VI Olimpiady Matematycznej Gimnazjalistów, w których uczestniczyło 669 uczniów. Spośród nich 187 zostało zakwalifikowanych do zawodów stopnia III.

Dla każdej liczby naturalnej 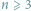można, oczywiście, narysować wielokąt, który ma 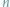 boków. A jak to będzie z wielościanami o zadanej z góry liczbie krawędzi?

Czasami, gdy zbytnio bujamy w obłokach, słyszymy od innych zejdź na ziemię! Kto by pomyślał, że ta zazwyczaj dość nieprzyjemna uwaga może być niekiedy cenną wskazówką do zadań ze stereometrii.

Pytanie postawione w tytule wydaje się dziwne. Przecież wiadomo co najmniej od czasów Platona, że wielościanów foremnych jest pięć typów: czworościan foremny, sześcian oraz ośmiościan, dwunastościan i dwudziestościan – wszystkie foremne. Łatwo też pokazuje się, że nie może być ich więcej. W czym zatem problem?

Polski namiot na francuskim Festiwalu Nauki był tak pełen gości, że miejsce dla jego matematycznej części życzliwie zostało ofiarowane przez Jeana Brette’a i jego kolegów w namiocie Pałacu Odkryć.