Proporcjonalność bez partii politycznych
Wyobraźmy sobie, że wyborcy chcą wybrać parlament o rozmiarze 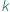 w małym kraju, w którym nie zaistniała jeszcze koncepcja partii politycznych (w związku z czym muszą głosować bezpośrednio na kandydatów, a nie na partie polityczne), albo że pracownicy pewnej firmy lub organizacji chcą wybrać
w małym kraju, w którym nie zaistniała jeszcze koncepcja partii politycznych (w związku z czym muszą głosować bezpośrednio na kandydatów, a nie na partie polityczne), albo że pracownicy pewnej firmy lub organizacji chcą wybrać 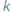 osób, które będą ich reprezentować w związkach zawodowych. Załóżmy, że każdy z wyborców głosuje, wskazując podzbiór kandydatów, których uważa za akceptowalnych: dla wyborcy
osób, które będą ich reprezentować w związkach zawodowych. Załóżmy, że każdy z wyborców głosuje, wskazując podzbiór kandydatów, których uważa za akceptowalnych: dla wyborcy 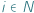 taki podzbiór akceptowalnych kandydatów będziemy oznaczać przez
taki podzbiór akceptowalnych kandydatów będziemy oznaczać przez 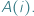 Pokażemy, że wskazanie "sprawiedliwego" sposobu przeprowadzenia takich wyborów jest nieoczywiste.
Pokażemy, że wskazanie "sprawiedliwego" sposobu przeprowadzenia takich wyborów jest nieoczywiste.


 kolarzy. Każdy pędzi z inną, ale stałą prędkością. Wystartowali z tego samego punktu, jadą w tym samym kierunku. Jest ciemno, nic nie widać, choć oko wykol...
kolarzy. Każdy pędzi z inną, ale stałą prędkością. Wystartowali z tego samego punktu, jadą w tym samym kierunku. Jest ciemno, nic nie widać, choć oko wykol...