Zawijanie i wycinanie dźwięków
Nagraliśmy ze znajomymi piosenkę. Nie było to profesjonalne przedsięwzięcie: nie wynajęliśmy studia nagraniowego, ale spotkaliśmy się u jednego z nas, wyjęliśmy instrumenty i zagraliśmy kilka razy do porządnego dyktafonu. Niestety, brak zawodowstwa dało się odczuć natychmiast - okazało się, że siedziałem na skrzypiącym krześle, które przy każdym moim ruchu robiło ziiik, ziiiiiik. Skrzypienie, choć nie permanentne, stanowczo utrudniało percepcję.

Na szczęście reżyserzy dźwięku dysponują narzędziami, które mogą "wyciąć", albo przynajmniej "schować", takie niepożądane odgłosy. Nie trzeba było więc spotykać się jeszcze raz i pamiętać, by siedzieć na innym krześle. Wystarczyło pozbyć się skrzypienia w trakcie obróbki nagrania. Taka operacja wycięcia zbędnego dźwięku jest możliwa dzięki narzędziu, które w skrócie nazwiemy FFT (Fast Fourier Transform, czyli Szybka Transformata Fouriera).
Żeby zobaczyć, jak działa FFT, zacznijmy od podstaw. Dźwięk to funkcja zmiany ciśnienia powietrza. Nie jest to jednak dowolna funkcja - ciśnienie podlega niewielkim zmianom, a dźwięki, przynajmniej te w przyjaznej dla ucha postaci, mają (mówiąc muzycznie) swoją wysokość, czyli (ściślej) odpowiadająca im funkcja zmiany ciśnienia powietrza jest funkcją okresową.
Każdą porządną funkcję okresową można przedstawić za pomocą szeregu Fouriera. W dużym uproszczeniu - jeśli funkcja 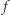 ma okres
ma okres 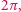 to da się ją przedstawić jako
to da się ją przedstawić jako 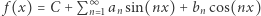 . Tego mocnego narzędzia teoretycznego nie można tu stosować ściśle, bo na ogół dźwięki zmieniają się w czasie, więc nie mamy do czynienia z funkcjami par excellence okresowymi. Wciąż są one jednak "okresowawe", to znaczy zmieniają się na tyle wolno, że można lokalnie sporządzić widmo dźwięku - czyli powiedzieć, które częstotliwości bazowe są istotne w danej chwili. Właśnie to widmo jest generowane przez FFT.
. Tego mocnego narzędzia teoretycznego nie można tu stosować ściśle, bo na ogół dźwięki zmieniają się w czasie, więc nie mamy do czynienia z funkcjami par excellence okresowymi. Wciąż są one jednak "okresowawe", to znaczy zmieniają się na tyle wolno, że można lokalnie sporządzić widmo dźwięku - czyli powiedzieć, które częstotliwości bazowe są istotne w danej chwili. Właśnie to widmo jest generowane przez FFT.
Spójrzmy na dwie postacie pierwszego dźwięku wspomnianej wcześniej piosenki - wykres drgania oraz odpowiadającego mu widma.

Rys. 1. Funkcja zmiany ciśnienia w czasie dla dźwięku struny gitarowej. Można w niej dostrzec pewną regularność, lecz trudno ją precyzyjnie opisać

Rys. 2. Widmo dźwięku z rysunku 1. Na osi 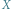 jest częstotliwość w Hz, na osi
jest częstotliwość w Hz, na osi 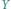 - amplituda drgania w danej częstotliwości
- amplituda drgania w danej częstotliwości
Rysunek 2 przedstawia udział danej częstotliwości w dźwięku z rysunku 1. Ten dźwięk nie jest funkcją okresową - każdy puls ma nieco inny kształt - jednak mimo to można spróbować skonstruować jego szereg Fouriera. Istotną rolę będą odgrywać w nim jedynie amplitudy 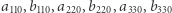 itd.
itd.
Razem z FFT pojawia się nowy punkt widzenia, niebywale przydatny w analizie dźwięku. Z rysunku 1 można od biedy wydedukować częstotliwość bazową, ale cała subtelność kształtu widma jest już nie do wychwycenia. Na rysunku 2 zupełnie jasne jest, że szósta składowa (ząbek o 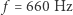 ) niemal nie istnieje, za to dziewiąta
) niemal nie istnieje, za to dziewiąta 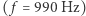 jest tak duża jak czwarta
jest tak duża jak czwarta 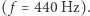 To, że takie fakty są w ogóle możliwe do zaobserwowania, jest kluczowe chociażby w analizie mowy.
To, że takie fakty są w ogóle możliwe do zaobserwowania, jest kluczowe chociażby w analizie mowy.
- Cały artykuł dostępny jest w wersji do druku: (1647 KB)
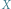 jest częstotliwość w Hz, na osi
jest częstotliwość w Hz, na osi 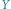 - amplituda drgania w danej częstotliwości
- amplituda drgania w danej częstotliwości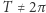 trzeba przeskalować
trzeba przeskalować  przez
przez 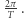
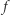 to nic innego, jak znajdowanie takich
to nic innego, jak znajdowanie takich 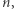 że wyrażenie
że wyrażenie 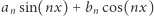 jest istotnym składnikiem funkcji
jest istotnym składnikiem funkcji