Co to jest?
Salamandry buszują w JOWach
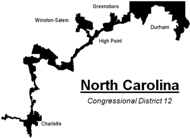
W końcu 2016 roku sąd okręgowy stanu Wisconsin po raz pierwszy w historii wyborów do Kongresu USA zdecydował o zmianie dystryktów wyborczych. Uzasadnieniem było to, że jednomandatowe dystrykty wyborcze dawały niesprawiedliwą przewagę Republikanom. Zdaniem sądu partia ta, mając przewagę w kongresie stanowym, po spisie powszechnym 2010 roku wyznaczyła dogodny dla siebie układ dystryktów.
Spis powszechny, ogłaszany w USA co 10 lat (począwszy od 1930 zawsze 1 kwietnia), ustala aktualną liczbę ludności w USA. Na jego podstawie, zgodnie z Konstytucją, określa się liczbę kongresmanów reprezentujących każdy stan w Izbie Reprezentantów.
W każdym stanie ustala się jednomandatowe dystrykty wyborcze (tytułowe JOWy). Liczba dystryktów odpowiada aktualnej liczbie reprezentantów danego stanu. Z wyjątkiem stanów, które reprezentuje jeden członek Izby Reprezentantów (np. Alaska czy Vermont), dystrykty w każdym stanie powinny być tak wybrane, by miały zbliżoną liczbę ludności, a ich kształt winien być zwarty i spójny.
Pierwszy z tych problemów, polegający na podziale mandatów według zadanej proporcji ludności w stanach, nie ma jednoznacznego rozwiązania. Pisałem o tym już w Delcie (Mandaty z urny). Drugi problem jest o wiele trudniejszy. Dystrykty powinny być tak wyznaczone, aby nie tylko spełniały wymagania co do równej liczby ludności, miały odpowiedni kształt, uwzględniały proporcje rasowe, nie dzieliły miast, ale i odzwierciedlały proporcjonalne poparcie partii politycznych w stanie.
Manipulowanie kształtem dystryktów w celu uzyskania nieproporcjonalnie korzystnego wyniku wyborów jednomandatowych nazwano gerrymanderingiem.
Gerrymandering jest coraz bardziej agresywny. Można konstruować wygodne dla siebie mapy, mając dostęp do danych o preferencjach wyborczych oraz wyspecjalizowanych narzędzi informatycznych (np. program Maptitude). Nastąpiło odwrócenie relacji: to nie wyborcy wybierają polityków, a politycy - wyborców.
Udowodnienie, że mamy do czynienia z tendencyjnym podziałem stanu na dystrykty, jest niezwykle trudne. Sędzia Sądu Najwyższego USA Justice Stewart powiadał: Gerrymandering jest jak pornografia - łatwo zobaczyć, trudno zdefiniować. Sąd Najwyższy w 2004 roku odrzucił wszystkie dowody na gerrymandering, nazywając go problemem nierozstrzygalnym.
W poszukiwanie metod wykrywania symptomów gerrymanderingu zaangażowali się również matematycy. Próbuje się zdefiniować, co to znaczy odpowiedni kształt dystryktu. Na Tufts University powstała grupa badawcza Metric Geometry and Gerrymandering Group. Co roku organizowany jest otwarty konkurs na prace, które pozwolą wykryć występowanie gerrymanderingu.
Problem gerrymanderingu dotyczy nie tylko USA, ale i innych krajów, nie wykluczając Polski. Wszędzie tam, gdzie mandaty ustalane są w jednomandatowych okręgach wyborczych, zagrożenie gerrymanderingiem jest możliwe.
Rys. 1
Gerrymandering
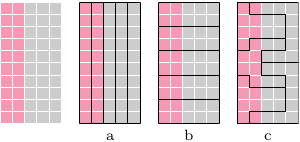
Oto przykład obszaru, składającego się z 50 obwodów wyborczych, w którym różowi mają 40% poparcia, a szarzy - 60%. Obszar należy podzielić na 5 równolicznych dystryktów.
Obszar można podzielić zgodnie z proporcją głosów różowych do szarych w całym obszarze (2:3) (Rys. 1a), dokładnie sprzecznie z tą proporcją (0:5 i 3:2) (Rys. 1b i Rys. 1c). Podział z rysunku 1b charakteryzuje się regularnymi kształtami dystryktów, a podział z rysunku 1c - nieregularnymi. Ze względu na kształty podział 1c nazwano by gerrymanderingiem. Niestety podział 1b nie zwróciłby niczyjej uwagi. Dopiero po wyborach okazałoby się, że podziały z rysunków 1b i 1c są manipulacją wyborczą. W rzeczywistości mamy czasami bardzo dziwny podział na dystrykty - przykłady dystryktów o fantazyjnych kształtach pokazano na rysunku 2.
Należy sobie odpowiedzieć na pytanie: czy jest to zmanipulowany podział, czy też stan ma takie ograniczenia ludnościowe lub geograficzne, że lepszych dystryktów nie da się wykreślić?
Rozwiązanie statystyczne
Naturalnym sposobem na stwierdzenie, czy przekroczono akceptowalny stopień gerrymanderingu, jest użycie testów statystycznych. Ich działanie podobne jest do matematycznego dowodu nie wprost. Bardzo upraszczając, dowód nie wprost polega na tym, że założenie, iż teza jest nieprawdziwa, prowadzi do fałszywego wniosku. W przypadku testów statystycznych uzasadnienie tezy, zwane w statystyce weryfikacją hipotezy roboczej (konkurencyjnej), polega na pokazaniu, że jej zaprzeczenie (hipoteza zerowa) prowadzi do mało prawdopodobnego, w świetle zebranych danych, wyniku.
Pierre Simon de Laplace na początku XIX wieku twierdził, że komety nie należą do Układu Słonecznego. Uzasadnienie tego stwierdzenia było statystyczne. Gdyby komety należały do Układu Słonecznego, to ich płaszczyzny orbitalne byłyby zbliżone do siebie, tak jak płaszczyzny orbitalne planet. Tymczasem obserwacje pokazywały, że płaszczyzny orbitalne komet były bardzo zróżnicowane. Jest więc mało prawdopodobnym, (Laplace nie wylicza tego prawdopodobieństwa), aby obiekty o tak zróżnicowanych orbitach należały do Układu Słonecznego.
Testy statystyczne są uznanym sposobem weryfikacji hipotez. W ten sposób uznano za udowodnione istnienie cząsteczki Higgsa, skuteczność aspiryny w profilaktyce ataków serca czy nawet fakt, że rakiety V2 atakowały przypadkowe punkty Londynu.
Podstawowym problemem w testowaniu jest obliczenie prawdopodobieństwa wystąpienia nietypowych obserwacji (w "teście" Laplace'a: zróżnicowanych orbit komet), gdy prawdziwa jest hipoteza zerowa (np. że komety pochodzą z Układu Słonecznego). Obliczenia te mogą nie być proste z wielu powodów. Z jednej strony, należy określić symptomy (testy) nietypowych obserwacji, a z drugiej - znaleźć rozkład prawdopodobieństwa tych symptomów przy założeniu, że hipoteza zerowa jest prawdziwa.
W większości praktycznych sytuacji trudno jest znaleźć odpowiedni rozkład teoretyczny. Stosuje się wtedy techniki intensywnie wykorzystujące moc obliczeniową komputerów. Do nich należą metody Monte Carlo oraz metoda 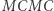 (Monte Carlo Markov Chain).
(Monte Carlo Markov Chain).
Symptomy gerrymanderingu
W praktyce prawniczej tylko niektóre z wielu proponowanych symptomów zyskały popularność.
Asymetria
Nietrudno zauważyć, że nawet mając mniejsze poparcie w obszarze, który będzie dzielony na dystrykty, można uzyskać przewagę mandatów na swoją korzyść. Metoda "dzielenie i pakowanie" polega na tym, że tworzy się dystrykty dla przeciwnika, wybierając do nich jak największą liczbę obwodów, w których ma on przewagę ("pakowanie"). Pozostałe dystrykty tworzy się tak, aby uzyskać w nich minimalną przewagę, rozdzielając równomiernie obwody przeciwnika ("dzielenie").
Rozkład głosów na partię, której głosy zostały odpowiednio upakowane i podzielone w dystryktach, charakteryzuje się tym, że przeważają w nim wartości małe, a wartości duże i bardzo duże są rzadkie. Taki rozkład nazywany jest w statystyce dodatnio asymetrycznym (np. rozkład dochodów czy ciśnienia krwi u pacjentów).
W przykładowym podziale (Rys. 1c) obwody szare upakowano do dwóch dystryktów, w każdym z nich 9 szarych i 1 różowy obwód. Pozostałych 12 szarych i 18 różowych obwodów rozdzielono równo między trzy dystrykty. Powstały trzy dystrykty z 60-procentową wygraną różowych i dwa z 90-procentową przewagą szarych. Wybory wygrywają różowi w stosunku 3:2, mimo że w całym obszarze oddano na nich tylko 40% głosów. Rozkład wyników dla szarych 40, 40, 40, 90, 90 jest dodatnio asymetryczny.
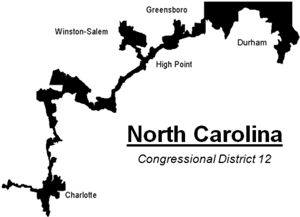
W wyborach z 2012 roku w Pensylwanii rozkład głosów oddanych na Demokratów w 18 dystryktach był dodatnio asymetryczny.
Mimo że w całym stanie poparcie dla Demokratów było nieznacznie większe (50,28% głosów), to uzyskała ona tylko 5 mandatów ( 27,78% ). Rządząca w Pensylwanii partia Republikańska tak rozdzieliła dystrykty, że znaczące poparcie na Demokratów skupiło się w 5 dystryktach, a w pozostałych 13 z niewielką przewagą wygrali Republikanie.
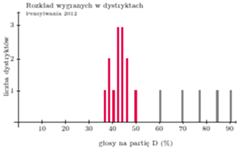
Rys. 3. Kolorami (czerwony - Republikanie, szary - Demokraci) oznaczono dystrykty, w których wygrała dana partia.
Wielkość asymetrii można zmierzyć różnicą między średnią arytmetyczną a medianą. Dla rozkładów dodatnio asymetrycznych ta różnica jest dodatnia, dla symetrycznych - równa 0. Takiej metody użyły niektóre sądy w Stanach Zjednoczonych, uznając, że występuje gerrymandering, gdy ta różnica jest duża.
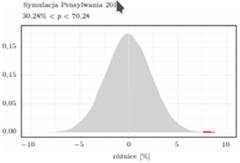
W przypadku wyborów w Pensylwanii różnica między średnią a medianą wśród danych z 18 dystryktów wynosiła 7,71%. Czy ta różnica jest duża? Zgodnie z metodologią testowania należałoby ocenić, jakie byłoby prawdopodobieństwo przekroczenia tej wartości, gdyby rozkład głosów na Demokratów w 18 dystryktach był symetryczny wokół 50,28%. Przyjmując, że procent głosów w dystryktach ma rozkład jednostajny w przedziale (30,28; 70,28), prawdopodobieństwo, że różnica między średnią a medianą jest większa niż 7,71% , wynosi 0,0004.
Wniosek: Jest niezwykle mało prawdopodobne, aby w tej sytuacji rozkład wyników głosowania na Demokratów był symetryczny wokół 50,28%.
Rys. 4
Na rysunku 4 przedstawiony jest rozkład różnic między średnią a medianą w 18 dystryktach, przy założeniu symetrii rozkładu głosów na Demokratów ze średnią 50,28%. Ledwo widoczny czerwony obszar na prawo od 7,71 odpowiada prawdopodobieństwu osiągniętego wyniku w wyborach przy tym założeniu.
Rozwlekłość
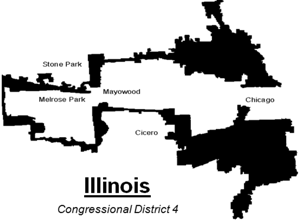
Zauważono, że w stanach z dystryktami o dziwnych, rozwlekłych kształtach dochodzi do niesprawiedliwego podziału mandatów. Sąd Najwyższy USA wielokrotnie powtarzał w swoich ocenach, że dziwnie wyglądające kształty są wskaźnikami złych intencji.
Aby ocenić stopień tej manipulacji, należałoby znaleźć jakiś "wskaźnik dziwności kształtu". Jednym ze stosowanych jest wskaźnik Polsby'ego-Poppera (wskaźnik 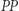 ), będący stosunkiem pola powierzchni dystryktu do pola koła o obwodzie równym obwodowi dystryktu. Z nierówności izoperymetrycznej wynika, że wskaźnik ten nigdy nie przekracza 1 - wartości dla koła, czyli obszaru idealnie "niedziwnego".
), będący stosunkiem pola powierzchni dystryktu do pola koła o obwodzie równym obwodowi dystryktu. Z nierówności izoperymetrycznej wynika, że wskaźnik ten nigdy nie przekracza 1 - wartości dla koła, czyli obszaru idealnie "niedziwnego".
Jednak nie zawsze małe wartości 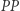 wskazują na zafałszowanie, a duże na poprawność wyborów. Podział z rysunku 1a, gdzie dystrykty są najbardziej wydłużone (wskaźnik
wskazują na zafałszowanie, a duże na poprawność wyborów. Podział z rysunku 1a, gdzie dystrykty są najbardziej wydłużone (wskaźnik 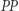 jest najmniejszy i wynosi około 0,26), idealnie odpowiada proporcjom głosów. Podział z rysunku 1b (
jest najmniejszy i wynosi około 0,26), idealnie odpowiada proporcjom głosów. Podział z rysunku 1b ( 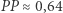 jest największy) skrajnie zafałszowuje proporcje głosów.
jest największy) skrajnie zafałszowuje proporcje głosów.
Niezgodność głosów i mandatów wskaźnik EG
Najbardziej przemawiającym do wyobraźni jest wskaźnik 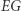 (Efficiency Gap - wskaźnik niewykorzystanych głosów). Wskaźnik ten liczy frakcję różnicy niewykorzystanych przez partie głosów w stosunku do ogólnej liczby oddanych głosów. Gdy partia zdobywa mandat w danym dystrykcie, to głosy niewykorzystane są nadwyżką nad połową głosów niezbędną do jego uzyskania. Gdy partia nie zdobywa mandatu, to wszystkie oddane na nią głosy są niewykorzystane. (Wadom i zaletom wskaźnika EG poświęcony jest artykuł Jak wykryć salamandrę z Delty 04/2018).
(Efficiency Gap - wskaźnik niewykorzystanych głosów). Wskaźnik ten liczy frakcję różnicy niewykorzystanych przez partie głosów w stosunku do ogólnej liczby oddanych głosów. Gdy partia zdobywa mandat w danym dystrykcie, to głosy niewykorzystane są nadwyżką nad połową głosów niezbędną do jego uzyskania. Gdy partia nie zdobywa mandatu, to wszystkie oddane na nią głosy są niewykorzystane. (Wadom i zaletom wskaźnika EG poświęcony jest artykuł Jak wykryć salamandrę z Delty 04/2018).
Na rysunku 1a różowi stracili po 5 głosów w dwóch dystryktach, szarzy - po 5 głosów w trzech. Różnica 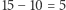 głosów dla szarych oznacza, że nie wykorzystali oni
głosów dla szarych oznacza, że nie wykorzystali oni 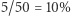 wszystkich głosów. Jest to właśnie współczynnik
wszystkich głosów. Jest to właśnie współczynnik 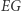 dla szarych (dla różowych wynosi on -10%). Jak widać,
dla szarych (dla różowych wynosi on -10%). Jak widać, 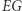 nie oddaje poprawnego podziału na dystrykty w tym przypadku. Lepiej byłoby, gdyby stracone głosy były liczone proporcjonalnie do zasobu głosów danej partii na całym obszarze (stanie). Tu różowi stracili
nie oddaje poprawnego podziału na dystrykty w tym przypadku. Lepiej byłoby, gdyby stracone głosy były liczone proporcjonalnie do zasobu głosów danej partii na całym obszarze (stanie). Tu różowi stracili 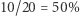 swoich głosów, szarzy
swoich głosów, szarzy 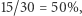 więc skorygowany współczynnik
więc skorygowany współczynnik 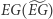 wynosi 0%. Mimo wielu niekorzystnych własności
wynosi 0%. Mimo wielu niekorzystnych własności  wysokie wartości tego wskaźnika (powyżej 7%) są przyjęte jako argument sądowy przemawiający za gerrymanderingiem.
wysokie wartości tego wskaźnika (powyżej 7%) są przyjęte jako argument sądowy przemawiający za gerrymanderingiem.
Anthony Kennedy, sędzia Sądu Najwyższego USA, zalecał użycie 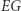 jako obiektywnego testu:
jako obiektywnego testu:
Setka różnych sędziów może badać te same mapy i pod warunkiem, że są oni biegli w arytmetyce, dojdą oni do identycznych konkluzji, czy mapy mieszczą się w dopuszczalnym zakresie i które z nich należy uznać za niekonstytucyjne.
(cyt. za: ballotpedia.org).
Metoda MCMC - test 
Rozkład prawdopodobieństwa symptomów gerrymanderingu jest trudny do wyznaczenia głównie z powodów geograficzno-politycznych. Lista wszystkich możliwych podziałów na dystrykty w danym stanie spełniających prawnie wymagane warunki spójności, reprezentatywności rasowej i niepodzielności miast jest trudna do ustalenia.
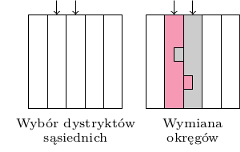
Rys. 5
Oszacowanie prawdopodobieństwa wystąpienia symptomu gerrymanderingu na zaobserwowanym poziomie jest możliwe dzięki algorytmowi "pełzającego" generowania map podziału na dystrykty i twierdzeniu udowodnionemu przez Wesleya Pegdena i innych.
Algorytm startuje od mapy, która podlega ocenie. W kolejnych krokach nowa mapa powstaje przez wymianę pary losowo wybranych obwodów na granicy dwóch losowo wybranych sąsiadujących ze sobą dystryktów. Jeśli ta wymiana prowadziłaby do podziału prawnie niedozwolonego, losowanie powtarza się aż do skutku. Ciąg map utworzonych w kolejnych krokach tworzy łańcuch Markowa.
Twierdzenie (Pegden, test 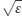 ). Niech
). Niech 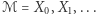 będzie odwracalnym, nieprzywiedlnym łańcuchem Markowa o stacjonarnym rozkładzie stanów
będzie odwracalnym, nieprzywiedlnym łańcuchem Markowa o stacjonarnym rozkładzie stanów 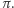 Przypuśćmy, że stanom
Przypuśćmy, że stanom  przypisano etykiety o wartościach rzeczywistych.
przypisano etykiety o wartościach rzeczywistych.
- Jeżeli
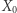 ma rozkład
ma rozkład 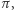 wtedy dla każdego ustalonego
wtedy dla każdego ustalonego 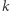 prawdopodobieństwo, że etykieta
prawdopodobieństwo, że etykieta 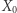 jest
jest  -outlierem pośród etykiet przypisanych trajektorii
-outlierem pośród etykiet przypisanych trajektorii 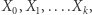 nie przekracza
nie przekracza 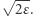
- Etykieta
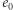 jest
jest  -outlierem dla ciągu etykiet
-outlierem dla ciągu etykiet 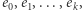 gdy
gdy 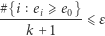
Gdy na bazie mapy 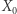 wygenerujemy 1000 map i
wygenerujemy 1000 map i 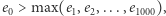 to prawdopodobieństwo, że
to prawdopodobieństwo, że 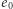 osiągnęło przypadkowo tak dużą wartość, jest mniejsze niż 0,045. Gdy wśród 1000 dodatkowo wygenerowanych map pięć będzie miało wartości co najmniej takie jak
osiągnęło przypadkowo tak dużą wartość, jest mniejsze niż 0,045. Gdy wśród 1000 dodatkowo wygenerowanych map pięć będzie miało wartości co najmniej takie jak 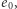 to mapa
to mapa 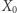 nie może być uważana za zmanipulowaną, gdyż prawdopodobieństwo takiego wyniku wynosi 0,11, co jest stosunkowo wysokim prawdopodobieństwem.
nie może być uważana za zmanipulowaną, gdyż prawdopodobieństwo takiego wyniku wynosi 0,11, co jest stosunkowo wysokim prawdopodobieństwem.
Z twierdzenia Pegdena można też oszacować, ile "pełzających" map należy wykonać, aby uzyskać zadany poziom dziwności tej mapy (zwany w statystyce poziomem istotności). Aby prawdopodobieństwo, że duża wartość etykiety 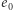 jest przypadkowa, nie przekroczyło 0,05, należy wygenerować więcej niż
jest przypadkowa, nie przekroczyło 0,05, należy wygenerować więcej niż 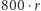 map takich, że spośród nich dokładnie
map takich, że spośród nich dokładnie 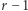 etykiet ma wartość co najmniej tak dużą jak
etykiet ma wartość co najmniej tak dużą jak 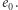 Analizując tą metodą podział Pensylwanii na dystrykty w 2012 roku, obliczono, iż prawdopodobieństwo, że obserwowane wartości różnicy między średnią i medianą są przypadkowo tak duże, jest mniejsze niż 0,0004. Oznacza to silne argumenty za wystąpieniem gerrymanderiungu. Wymagało to bardzo wielu godzin pracy silnych komputerów.
Analizując tą metodą podział Pensylwanii na dystrykty w 2012 roku, obliczono, iż prawdopodobieństwo, że obserwowane wartości różnicy między średnią i medianą są przypadkowo tak duże, jest mniejsze niż 0,0004. Oznacza to silne argumenty za wystąpieniem gerrymanderiungu. Wymagało to bardzo wielu godzin pracy silnych komputerów.
Finał
Rozstrzyganie o możliwości wystąpienia gerrymanderingu wymusza na sądach użycie coraz bardziej skomplikowanych metod matematycznych i statystycznych. Wykraczają one daleko poza umiejętności arytmetyczne, o których mówił sędzia Kennedy.
Tradycyjne sądownictwo broni się przed takimi nowinkami. Nawet wskaźnik  spotyka się z oporem. Jeden z sędziów argumentował, że trudność w zrozumieniu tego wskaźnika, z jaką społeczeństwo mogłoby się spotkać, doprowadziłaby ostatecznie do osłabienia wiarygodności sądu. Inny z kolei powiada:
spotyka się z oporem. Jeden z sędziów argumentował, że trudność w zrozumieniu tego wskaźnika, z jaką społeczeństwo mogłoby się spotkać, doprowadziłaby ostatecznie do osłabienia wiarygodności sądu. Inny z kolei powiada:
Może to po prostu wynikać z mojego wykształcenia, ale mogę ten wskaźnik opisać tylko jako socjologiczny bełkot.
W reakcji na takie wypowiedzi w kwietniu 2018 roku pojawiła się na Uniwersytecie Princeton praca pod tytułem Antidotum na bełkot. Propozycja zestawu narzędzi dla sędziów do testowania stronniczego gerrymanderingu. W pracy tej proponuje się m.in. użycie testu Studenta do oceny zagrożenia gerrymanderingiem. I na jej końcu pojawia się złośliwe stwierdzenie:
Skoro piwowarzy potrafią wykorzystać moc statystycznego rozumowania, z pewnością sędziowie też mogą.
Nadeszły ciekawe czasy dla prawników.
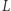 jest największe dla koła o obwodzie
jest największe dla koła o obwodzie 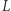 (p. artykuł
(p. artykuł 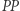 zależy też od skali mapy - im mniejsza skala, tym mniejsze wartości. Odpowiedzialny za to jest efekt fraktalny - im mniejsza skala, tym dłuższa jest linia brzegowa.
zależy też od skali mapy - im mniejsza skala, tym mniejsze wartości. Odpowiedzialny za to jest efekt fraktalny - im mniejsza skala, tym dłuższa jest linia brzegowa.