Alessio Figalli - Medal Fieldsa 2018

Alessio Figalli
Alessio Figalli, profesor (Eidgenössische Technische Hochschule) ETH w Zurychu, otrzymał Medal Fieldsa na Międzynarodowym Kongresie Matematyków w Rio de Janeiro za - jak napisano w uzasadnieniu - "wkład w teorię optymalnego transportu i jej zastosowania"...
Figalli po ukończeniu liceum klasycznego w Rzymie rozpoczął studia matematyczne w Scuola Normale Superiore w Pizie, gdzie po czterech latach uzyskał dyplom magistra pod kierunkiem Luigiego Ambrosio. Pracę doktorską przygotował w ciągu 18 miesięcy pod wspólnym kierunkiem profesorów Luigiego Ambrosio oraz Cédrica Villaniego (laureata Medalu Fieldsa z 2010 roku). Już w czasie studiów Figalli zainteresował się problemami optymalnego transportu (tego dotyczyła jego praca magisterska), a następnie pogłębiał temat w czasie studiów doktoranckich. Teoria ta, sięgająca swym początkiem czasów rewolucji francuskiej, zajmuje się problemem przeniesienia możliwie najtańszym kosztem pewnej masy rozłożonej (w ogólności niejednorodnie) w zbiorze 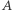 do zbioru
do zbioru 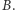 Ponieważ rozkład masy można interpretować jako rozkład prawdopodobieństwa, to zagadnienie transportowe można traktować jako problem odległości między dwoma rozkładami prawdopodobieństwa, gdzie metryką mierzącą tę odległość jest funkcja kosztu transportu. Takie ogólne sformułowanie zagadnienia, pozwalające na dowolne specyfikowanie funkcji kosztów, prowadzi do trudnych problemów matematycznych, a jednocześnie ma bardzo szerokie zastosowanie praktyczne w planowaniu przestrzennym, hydromechanice, biologii, analizie obrazów, ekonomii oraz wielu innych dziedzinach.
Ponieważ rozkład masy można interpretować jako rozkład prawdopodobieństwa, to zagadnienie transportowe można traktować jako problem odległości między dwoma rozkładami prawdopodobieństwa, gdzie metryką mierzącą tę odległość jest funkcja kosztu transportu. Takie ogólne sformułowanie zagadnienia, pozwalające na dowolne specyfikowanie funkcji kosztów, prowadzi do trudnych problemów matematycznych, a jednocześnie ma bardzo szerokie zastosowanie praktyczne w planowaniu przestrzennym, hydromechanice, biologii, analizie obrazów, ekonomii oraz wielu innych dziedzinach.
Alessio Figalli jest współautorem ponad 150 prac naukowych, trudno więc w krótkim tekście opisać nawet pobieżnie wszystkie jego osiągnięcia. W uzasadnieniu przyznania Medalu Fieldsa na pierwszym miejscu wymieniono prace dotyczące regularności rozwiązań równania Monge'a-Ampère'a oraz ich zastosowania do wykazania regularności rozwiązań pewnego modelu meteorologicznego (semigeostrophic model) wykorzystywanego do wielkoskalowych prognoz pogody. Model ten, zaproponowany przez meteorologów w latach dziewięćdziesiątych XX wieku, opisuje dynamiki frontów atmosferycznych (Figalli nazwał go "modelem ewolucji chmur"). Sens badania regularności rozwiązań takich modeli związany jest z faktem, że w praktyce często znaleźć można jedynie rozwiązania przybliżone, otrzymane metodą symulacji komputerowych. Takie symulacje oczywiście powinny być zbieżne do prawdziwego rozwiązania, a to można zagwarantować jedynie, gdy rozwiązanie jest jednoznaczne oraz dostatecznie regularne (dostatecznie wiele razy różniczkowalne). Alessio Figalli wspólnie ze współautorem Guido De Philippisem zbadali strukturę rozwiązań równania Monge'a-Ampère'a. Ich wynik ma głębokie matematyczne znaczenie, ponieważ otrzymane przez nich oszacowanie wzmacnia wcześniejszy rezultat Luisa A. Caffarelliego z roku 1900 (w kierunku pełnej nierówności Sobolewa).
Autorzy następnie wykazali, że równanie Monge'a-Ampère'a może być traktowane jako równanie optymalnego transportu gęstości chmur opisywanych modelem meteorologicznym. Pozwoliło to wykazać regularność rozwiązań modelu meteorologicznego i uzasadnić poprawność symulacji komputerowych dla tego modelu.
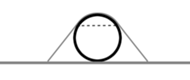
Weźmy okrągłą ramę i naciągnijmy na nią elastyczny materiał. Następnie nakryjmy tą ramą kulę leżącą na stole tak, żeby kula znalazła się dokładnie na środku tej ramy. Gdy rama znajdzie się na powierzchni stołu, to z boku sytuacja będzie wyglądać tak jak na rysunku. Przerywana szara linia to powierzchnia swobodna - miejsce, w którym materiał traci styczność z kulą. W rzeczywistości ta powierzchnia swobodna jest okręgiem.
Drugim osiągnięciem Alessio Figalliego, wymienionym w uzasadnieniu przyznania Medalu Fieldsa, są napisane w 2017 roku prace z Joaquimem Serrą, dotyczące problemów swobodnej powierzchni. Problem swobodnej powierzchni występuje w wielu zagadnieniach fizyki i techniki. Swobodne powierzchnie to na przykład powierzchnia kostki lodu rozpuszczającej się w szklance napoju lub powierzchnia falującego morza. Najprościej można sobie wyobrazić swobodną powierzchnię, rozpatrując elastyczną membranę naciągniętą na okrągłą ramę, którą nakrywamy kulę leżącą na powierzchni stołu. Membrana częściowo dotyka powierzchni kuli, a częściowo wisi w powietrzu. Granica obszaru styku membrany z powierzchnią kuli jest właśnie swobodną powierzchnią. Oczywiście w tym prostym przykładzie swobodna powierzchnia jest okręgiem, którego rozmiar zależy od wymiarów kuli oraz ramy, na której rozciągnięta jest membrana. Dla bardziej skomplikowanych kształtów przeszkody, jaką tu była kula, rozwiązanie nie musi być już tak proste. Zasadnicze jest pytanie o stopień gładkości swobodnej powierzchni. W 1977 roku Luis Caffarelli wykazał, że swobodna powierzchnia jest gładka poza zbiorem punktów osobliwych. Przez następne lata matematycy badali charakter tego zbioru punktów osobliwych. Figalli i Serra znaleźli optymalną charakteryzację tego zbioru (zbyt obszerną, aby ją tu dokładnie przytaczać). W szczególności, w przypadku 3-wymiarowym pokazali, że swobodna powierzchnia jest gładka z wyjątkiem izolowanych punktów osobliwych.
Przywołajmy tu jedną z wcześniejszych prac Alessio Figalliego, napisaną wspólnie z Francesco Maggim i Aldo Pratellim, dotyczącą wykorzystania teorii optymalnego transportu w dowodzie nierówności izoperymetrycznych. Klasyczny problem izoperymetryczny polega na znalezieniu optymalnego kształtu obszaru, którego brzeg minimalizuje napięcie powierzchniowe. Przykładem rozwiązania takiego problemu są bańki mydlane, które ograniczają daną objętość powietrza powłoką o minimalnej powierzchni. Bardziej interesujące jest badanie problemu izoperymetrycznego dla kryształów, gdzie rozwiązanie jest bardziej skomplikowane, ponieważ kryształ przyjmuje kształt minimalizujący energię pochodzącą od oddziaływań między atomami. Otrzymana we wspomnianej pracy nierówność izoperymetryczna pozwala odpowiedzieć na pytanie, jak zmienia się kształt kryształu, kiedy układowi zostanie dodana pewna energia (np. kryształ zostanie podgrzany). Aby uzyskać odpowiedź, należy spojrzeć na zmianę kształtu kryształu jak na problem transportu ze stanu początkowego (o minimalnej energii) do stanu po dodaniu energii. Wynik Figalliego, Maggi i Pratelliego mówi, że zmiana kształtu jest proporcjonalna do pierwiastka z dodanej energii. Ten zaskakująco prosty wynik został uzupełniony o bardzo wartościowy z fizycznego punktu widzenia rezultat, że ta zmiana kształtu jest stabilna, czyli małemu dodatkowi energii odpowiada mała zmiana kształtu. Co więcej, ponieważ uzyskana nierówność izoperymetryczna jest optymalna, więc zmiana kształtu nie może być większa niż to wynika z ich oszacowania.

Alessio Figalli jest matematykiem o niezwykle bogatym doświadczeniu międzynarodowym. Po studiach doktoranckich, które spędził między Scuola Normale Superiore w Pizie a École Normale Supérieure w Lyonie, podjął pracę na uniwersytecie w Nicei oraz w oddziale Centre National de la Recherche Scientifique (CNRS) przy tym uniwersytecie. Po roku przeniósł się na stanowisko profesora w École Polytechnique w Palaiseau pod Paryżem. W latach 2009-2016 pracował na różnych stanowiskach profesorskich na uniwersytecie w Austin (University of Texas at Austin), aby w roku 2016 przyjąć stanowisko profesora zwyczajnego w ETH w Zurychu. Figalli ma bardzo liczną grupę międzynarodowych współpracowników, których chętnie odwiedza, nie odczuwając trudności dalekich podróży lotniczych, a także przyjmując ich wizyty w Zurychu. Promotor jego doktoratu i współautor publikacji, Cédric Villani, podkreślał w jednym z wywiadów, że fakt, iż na edukację matematyczną Figalliego złożyło się doświadczenie wyniesione z wielu ośrodków (z widocznym głównym wpływem szkoły włoskiej i francuskiej), miał znaczący wpływ na jego matematyczne sukcesy. Na zakończenie należy dodać, że współpracownicy Figalliego zgodnie podkreślają jego niezwykłą szybkość i biegłość w pracy nad technicznymi detalami oraz umiejętność sprawnego wyczuwania istoty nowych problemów. Jest on także znany z otwartości i przyjacielskiego stosunku do młodych kolegów i studentów. Wszystkie te cechy czynią z Alessio Figalliego matematyka, którego dalsza kariera rysuje się niezwykle obiecująco.
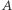 przez kwadrat długości jego brzegu. Problem sięga swoją historią do starożytnej legendy o tym, jak królowa Dydona uzyskała ziemię pod budowę Kartaginy. W wersji bardziej pasującej do problemu rozważanego przez Figalliego możemy myśleć o trójwymiarowym zbiorze
przez kwadrat długości jego brzegu. Problem sięga swoją historią do starożytnej legendy o tym, jak królowa Dydona uzyskała ziemię pod budowę Kartaginy. W wersji bardziej pasującej do problemu rozważanego przez Figalliego możemy myśleć o trójwymiarowym zbiorze 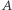 wypełnionym płynem o pewnej energii wewnętrznej. Ubytek tej energii jest związany z wypływem płynu ze zbioru
wypełnionym płynem o pewnej energii wewnętrznej. Ubytek tej energii jest związany z wypływem płynu ze zbioru 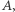 co jest zależne od powierzchni brzegu zbioru
co jest zależne od powierzchni brzegu zbioru 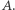 Informacja o ubytku energii pozwala kontrolować powierzchnię brzegu
Informacja o ubytku energii pozwala kontrolować powierzchnię brzegu