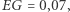Jak wykryć salamandrę?
Przyjrzyjmy się problemowi, przed którym staje legislator wyborczy: podział kraju na okręgi wyborcze...
Ordynacja wyborcza występująca w Stanach Zjednoczonych przy House of Representative polega na wybraniu 435 kandydatów z 50 stanów. Każdy stan podzielony jest na jednomandatowe okręgi zwane też dystryktami. W każdym dystrykcie dokładnie jedna partia wygrywa, zdobywając miejsce w House of Representative. Okręgi są zdefiniowane przez terytorium, powinny być spójne oraz mieć taką samą populację. Liczba okręgów w danym stanie podyktowana jest populacją i już ona jest przedmiotem wielu dyskusji. Więcej na ten temat można znaleźć w literaturze pod nazwą apportionment. Upraszczając nieco problem, przeanalizujemy, w jaki sposób sprawiedliwie dokonać podziału na okręgi wyborcze.
Okazuje się, że manipulując podziałem na okręgi, nie zmieniając liczby wyborców w okręgach, można zmienić wyniki wyborów. Manipulacja w tym zakresie nazywa się gerrymanderingiem. Nazwa jest zbitką nazwiska amerykańskiego polityka Elbridge'a Gerry'ego oraz salamandry. W 1812 roku E. Gerry, jako gubernator stanu Massachusetts, zarządził podział stanu na dystrykty w taki sposób, aby zapewnić przewagę Partii Demokratyczno-Republikańskiej. Jeden z okręgów przypominał mityczną salamandrę i został określony przez Boston Gazette jako Gerry-mander. Od tego czasu problem nie zniknął, Stany Zjednoczone stale podejmują działania mające walczyć z tym problemem.
Wprowadzenie wskaźnika
Dla uproszczenia przyjmijmy, że w wyborach kandydują tylko 2 partie: 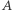 i
i 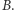 Wygrywają one miejsca w rządzie, które potem we własnym zakresie rozdzielają. Zakładamy, że okręgi są jednomandatowe (ich liczba
Wygrywają one miejsca w rządzie, które potem we własnym zakresie rozdzielają. Zakładamy, że okręgi są jednomandatowe (ich liczba 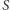 jest ustalona z góry), że w każdym jest taka sama liczba wyborców oraz że w każdym ważne głosy oddaje dokładnie tyle samo osób. Zbiór okręgów oznaczmy przez
jest ustalona z góry), że w każdym jest taka sama liczba wyborców oraz że w każdym ważne głosy oddaje dokładnie tyle samo osób. Zbiór okręgów oznaczmy przez 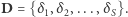 Przyjmijmy następujące oznaczenia:
Przyjmijmy następujące oznaczenia:
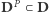 - zbiór okręgów, w których wygrała partia
- zbiór okręgów, w których wygrała partia 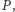
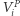 - liczba głosów zdobytych przez partię
- liczba głosów zdobytych przez partię 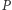 w okręgu
w okręgu 
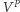 - całkowita liczba głosów oddanych na partię
- całkowita liczba głosów oddanych na partię 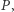
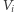 - liczba wszystkich głosów oddanych w okręgu
- liczba wszystkich głosów oddanych w okręgu 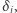
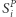 - liczba miejsc zdobytych przez partię
- liczba miejsc zdobytych przez partię 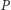 w
w 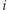 -tym okręgu
-tym okręgu 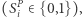 item
item 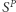 - liczba wszystkich miejsc zdobytych przez partię
- liczba wszystkich miejsc zdobytych przez partię 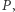
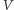 - liczba wszystkich głosów oddanych w wyborach.
- liczba wszystkich głosów oddanych w wyborach.
Zatem głosów oddanych w każdym okręgu jest dokładnie 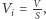 dla
dla 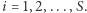 Wskaźniki
Wskaźniki 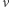 i
i 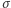 oznaczają przewagę partii
oznaczają przewagę partii 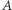 odpowiednio w głosach, które oddali wyborcy oraz miejscach, które uzyskała:
odpowiednio w głosach, które oddali wyborcy oraz miejscach, które uzyskała:

Głosami zmarnowanymi (wasted votes) nazywamy wszystkie głosy na przegraną partię oraz na wygraną powyżej progu 50% (tzn. te, które były zbędne do zwycięstwa). Oznacza to, że zawsze połowa głosów jest zmarnowana.

Analogicznie jak poprzednio, niech 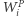 to będzie liczba głosów zmarnowanych w okręgu
to będzie liczba głosów zmarnowanych w okręgu 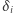 przez głosujących na partię
przez głosujących na partię 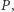 zaś
zaś 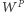 - liczba zmarnowanych głosów we wszystkich okręgach. Zachodzi następująca zależność
- liczba zmarnowanych głosów we wszystkich okręgach. Zachodzi następująca zależność 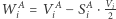 (przypomnijmy, że okręgi są jednomandatowe). Spójrzmy, jak wyglądają głosy zmarnowane na partie
(przypomnijmy, że okręgi są jednomandatowe). Spójrzmy, jak wyglądają głosy zmarnowane na partie 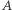 i
i 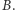 W tym celu zdefiniujmy współczynnik efficiency gap
W tym celu zdefiniujmy współczynnik efficiency gap

Jeżeli 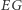 jest dodatnie, oznacza ono niesprawiedliwość wobec partii
jest dodatnie, oznacza ono niesprawiedliwość wobec partii 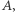 gdy ujemne, to dla
gdy ujemne, to dla 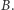 Gdy
Gdy 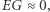 wówczas obie partie straciły podobną liczbę głosów i taką sytuację uznaje się za sprawiedliwą.
wówczas obie partie straciły podobną liczbę głosów i taką sytuację uznaje się za sprawiedliwą.
Przyjrzyjmy się bliżej informacji, którą niesie współczynnik 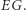 Zauważmy, że
Zauważmy, że

stąd

Niektóre usterki współczynnika 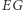 :
:
- Współczynnik
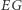 nie odwzorowuje proporcji głosów w liczbie zdobytych miejsc. Tzn. jeśli partia
nie odwzorowuje proporcji głosów w liczbie zdobytych miejsc. Tzn. jeśli partia 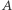 zdobywa w całym kraju 66% głosów, zaś partia
zdobywa w całym kraju 66% głosów, zaś partia 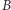 uzyskała 34%, to wówczas
uzyskała 34%, to wówczas 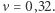 Aby współczynnik
Aby współczynnik 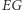 był jak najbliższy 0, to
był jak najbliższy 0, to 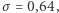 czyli partia
czyli partia 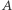 powinna zdobyć 82% miejsc, zaś partia
powinna zdobyć 82% miejsc, zaś partia 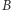 tylko 18%.
tylko 18%. - Jeśli partia
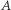 będzie miała co najmniej 79% poparcia w społeczeństwie, to niezależnie jak wybierzemy okręgi, będzie
będzie miała co najmniej 79% poparcia w społeczeństwie, to niezależnie jak wybierzemy okręgi, będzie 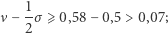
wybory zawsze byłyby więc niesprawiedliwe (jeśli uznamy, że takie są wtedy, gdy
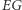 przekracza
przekracza 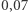 ). Wynika to z tego, że przewaga wygranych miejsc ma
). Wynika to z tego, że przewaga wygranych miejsc ma 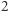 razy mniejsze znaczenie od przewagi głosów w społeczeństwie.
razy mniejsze znaczenie od przewagi głosów w społeczeństwie. - Dla okręgu
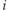 poziom sprawiedliwości
poziom sprawiedliwości 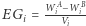 wynosi zero tylko wtedy, gdy jedna partia zdobędzie
wynosi zero tylko wtedy, gdy jedna partia zdobędzie 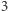 razy więcej głosów od drugiej. Wtedy sprawiedliwym podziałem jest taki, w którym w każdym z okręgów proporcje głosów wynoszą
razy więcej głosów od drugiej. Wtedy sprawiedliwym podziałem jest taki, w którym w każdym z okręgów proporcje głosów wynoszą 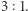
Zachęcamy do przyjrzenia się nieco poprawionej metodzie mierzenia niesprawiedliwości

Nie istnieje jednoznaczny, powszechnie stosowany sposób sprawdzania, czy podział jest sprawiedliwy. W Stanach Zjednoczonych powoływane są specjalne zespoły czuwające nad takimi podziałami. Zauważmy, że nie wszystkie założenia przytoczonego modelu daje się spełnić (np. równa liczba wyborców w każdym okręgu i jednocześnie równa liczba oddanych głosów), stąd pole do poprawy modelu jest jeszcze spore.
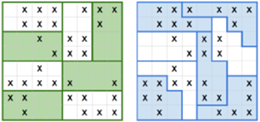
Z lewej współczynnik 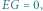 z prawej wynosi
z prawej wynosi 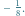
Przykład 1. Każde pole planszy przedstawia jednego głosującego.  oznacza głos oddany na partię
oznacza głos oddany na partię 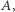 puste pole to głos oddany na partię
puste pole to głos oddany na partię 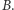 Na rysunku z lewej obie partie zdobywają taką samą liczbę mandatów. Jeśli jednak zmienimy kształt okręgów tak jak na rysunku z prawej strony, to wygra partia
Na rysunku z lewej obie partie zdobywają taką samą liczbę mandatów. Jeśli jednak zmienimy kształt okręgów tak jak na rysunku z prawej strony, to wygra partia 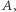 zdobywając 5 mandatów.
zdobywając 5 mandatów.
Przykład 2. Można znaleźć przykład takich wyników głosowania na dwie partie, żeby w jednym układzie okręgów wygrała partia 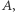 a w innym
a w innym 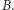
Przykład 3. Czy możliwe jest, żeby sytuacja z przykładu 2 miała miejsce, gdy okręgi są dwumandatowe?
Przykład 4. W 2015 roku w USA odbyła się rozprawa pod nazwą "Gill v. Whitford", w której sąd najwyższy zgodnie z radą pomysłodawców efficiency gap zasądził, że maksymalny dopuszczalny poziom 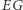 to
to 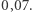 Tym samym stwierdzono, że wybory z 2012 i 2014 roku w Wisconsin były niekonstytucyjne (
Tym samym stwierdzono, że wybory z 2012 i 2014 roku w Wisconsin były niekonstytucyjne ( 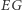 wyniosło odpowiednio
wyniosło odpowiednio 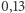 oraz
oraz 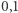 ).
).
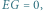 z prawej wynosi
z prawej wynosi