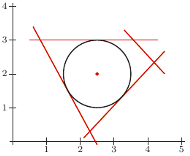
Na rysunku przedstawiony jest największy okrąg mieszczący się w kolorowym czworokącie. Środek tego okręgu jest środkiem Czebyszewa kolorowego czworokąta.

Zadanie znalezienia największego okręgu, który można wpisać w wielokąt, jest równoważne zadaniu znalezienia punktu o największej odległości od brzegu tego wielokąta. Jeden z algorytmów numerycznych, który wydaje się skuteczny przy rozwiązywaniu tego zagadnienia, nazywany jest algorytmem sekwencyjnym. Polega on na wybraniu kandydata na poszukiwany środek Czebyszewa, skonstruowaniu pewnej siatki węzłów dookoła kandydata (w sposób deterministyczny bądź losowy) i wskazaniu węzła o największej odległości od brzegu. Węzeł ten staje się nowym kandydatem na środek Czebyszewa, wokół którego konstruowana jest nowa, odpowiednio "ciaśniejsza" siatka. Procedura ta powtarzana jest aż do osiągnięcia pożądanej precyzji. Opisaną metodę można stosować do dowolnie wybranych wielokątów, co jest jej zdecydowaną zaletą, niestety, czasem nie prowadzi ona do znalezienia interesującego nas środka. Jeżeli ograniczymy się tylko do wielokątów wypukłych, zdecydowanie lepszym podejściem jest skorzystanie z programowania liniowego. Sprowadzając problem do odpowiedniego układu liniowych nierówności, w prosty sposób możemy dla dowolnego wielokąta wypukłego znaleźć największy okrąg weń wpisany, wykorzystując programowanie liniowe.

Można się teraz zastanowić, czy ten ciekawy problem geometryczny ma swoje zastosowanie w rzeczywistej praktyce. Otóż opisane wyżej metody stosuje się do wyznaczania tak zwanych biegunów niedostępności, czyli punktów na Ziemi o pewnych ekstremalnych cechach geograficznych. Na przykład, oceaniczny biegun niedostępności to punkt na oceanie najbardziej oddalony od lądu. Punkt ten został wyznaczony w 1992 roku, nazywa się "Nemo" i znajduje się na Oceanie Spokojnym, 2688 km od najbliższych wysp. Północny biegun niedostępności to niezwykle trudno dostępne miejsce na Oceanie Arktycznym, znajdujące się na paku lodowym (wieloletnim, dryfującym lodzie morskim), najbardziej oddalone od stałego lądu. Kontynentalnym biegunem niedostępności dla Eurazji jest oddalone o 2645 km od najbliższego wybrzeża miejsce w Chinach.

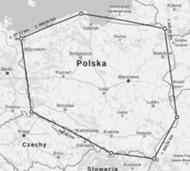
Przyjrzyjmy się temu zagadnieniu na przykładzie Polski. Jeśli kontur kraju przybliżymy wielokątem wypukłym, to posługując się metodami programowania liniowego, możemy odnaleźć środek Czebyszewa tego wielokąta, a zatem przybliżenie punktu najbardziej oddalonego od każdej z granic lądowych oraz wybrzeża. Wielokąt został wybrany jak na ilustracji obok. Pora na wyprowadzenie interesującego nas problemu liniowego.

Wybrany wielokąt ma siedem wierzchołków. Znajdujemy jego odzwierciedlenie w układzie kartezjańskim za pomocą kalkulatora geograficznego, dostępnego, na przykład na stronie www.piast.edu.pl (jednostką są metry). Teraz wyprowadźmy siedem nierówności, które opisują zadany wielokąt. Rozpatrzmy prostą, która przechodzi przez ten najbardziej wysunięty na północ z wybranych punktów: 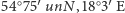oraz ten na północnym zachodzie 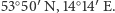W układzie kartezjańskim będą to punkty (934076,97; 6061855,94), (1155571,89; 6220125,62). Rozwiązując elementarny układ równań, otrzymujemy wzór szukanej prostej: Oczywiście, interesujący nas obszar znajduje się "pod" powyższą prostą, a zatem pierwsza z opisujących go nierówności powstaje poprzez zamianę znaku " " w powyższej równości na " 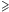". To samo robimy dla kolejnych sześciu boków wybranego wielokąta.

Gdy już znajdziemy siedem półpłaszczyzn, których przecięcie tworzy interesujący nas wielokąt, możemy w prosty sposób sprowadzić zadanie do programowania liniowego. Najpierw nierówności, które uzyskaliśmy w poprzednim kroku, przedstawiamy w postaci

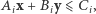gdzie 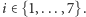Wybrany wielokąt wypukły można więc zapisać jako:

Zadanie polega, jak pamiętamy, na znalezieniu środka Czebyszewa 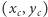oraz promienia koła 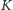o środku w 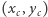- największego koła mieszczącego się w naszym wielokącie. Mamy zatem trzy nieujemne zmienne 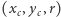oraz funkcję celu równą 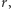którą będziemy maksymalizować na pewnym ograniczonym zbiorze.

Zwróćmy uwagę, że nierówność 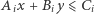dla każdego punktu 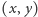w kole 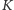zachodzi wtedy i tylko wtedy, gdy spełniona jest nierówność:

(*)

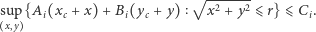Na mocy nierówności Cauchy'ego-Schwarza dostajemy 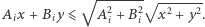W tej sytuacji nierówność 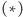może zostać zapisana jako

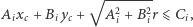a nasz problem można sformułować w prostej do rozwiązania przez program postaci: "Znajdź trójkę 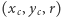w zbiorze

dla której wartość jest możliwie największa".

Powyższe zagadnienie można łatwo zaimplementować i szybko obliczyć w programie Sage (sagecell.sagemath.org/?q=egjobr). Okazuje się, że obliczając w ten sposób, miejsce w Polsce najbardziej oddalone od wszystkich granic jest położone we wsi Jackowice w województwie łódzkim, w odległości 24 km od uważanego za geometryczny środek Polski punktu w miejscowości Piątek.

Programowanie liniowe okazuje się skuteczną i prostą w użyciu metodą rozwiązywania wielu zagadnień. Tutaj pokazaliśmy, jak można stosować tę metodę do rozwiązywania ciekawych zadań geometrycznych, a pośrednio również problemów geograficznych.