Jednym z modeli zbiorowego podejmowania decyzji są funkcje społecznego dobrobytu. Załóżmy, że grupa 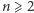osób 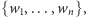nazwijmy ich wyborcami, chce podjąć wspólną decyzję w sprawie 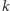różnych alternatyw (czyli możliwości). Zbiór wyborców oznaczmy przez 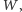natomiast zbiór alternatyw przez 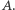Przyjmijmy, że każda z osób potrafi uporządkować zbiór alternatyw od najlepszej do najgorszej jej zdaniem alternatywy - przyporządkowując alternatywom liczby od 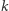(najlepsza) do 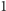(najgorsza). Zapis 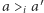oznacza, że wyborca 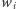uważa alternatywę 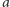za lepszą od alternatywy 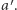Dla uproszczenia wykluczamy "remisy". Każda z osób ma zatem do wyboru 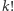możliwych uporządkowań - ich zbiór oznaczmy przez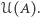

Funkcję 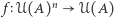nazywamy funkcją społecznego dobrobytu. Przyporządkowuje ona krotce 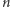uporządkowań alternatyw (odpowiadającym preferencjom wyborców 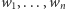) jedno uporządkowanie, które uznajemy za zbiorową decyzję. Zapis 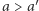oznacza, że grupa uznaje alternatywę 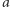za lepszą od alternatywy 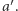Aby funkcję społecznego dobrobytu uznać za sprawiedliwą metodę podejmowania zbiorowych decyzji, wymaga się, by spełniała szereg warunków.

Postulat niezależności od alternatyw niezwiązanych głosi, że decyzja w sprawie alternatyw i 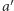nie powinna zależeć od preferencji wyborców wobec pozostałych kwestii.

Niezależność od alternatyw niezwiązanych. Przypuśćmy, że podejmując decyzję przy zastosowaniu funkcji 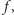grupa uznała alternatywę 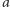za lepszą od alternatywy 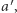czyli 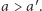Następnie niektórzy członkowie grupy zmienili zdanie w sprawie pewnych alternatyw, ale ich preferencje względem alternatyw 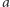i 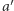pozostały takie same, tzn. zależność 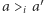albo 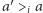dla każdego wyborcy 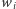pozostała bez zmian. Funkcja 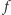spełnia warunek niezależności od alternatyw niezwiązanych, jeśli zawsze w takiej sytuacji, przy kolejnym podejmowaniu decyzji za pomocą funkcji 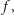grupa w dalszym ciągu uzna alternatywę 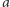za lepszą od alternatywy 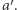Słaby warunek optymalności Pareto wymaga respektowania jednomyślnej preferencji członków grupy.

Słaby warunek optymalności Pareto. Załóżmy, że każdy członek grupy przedkłada alternatywę 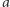nad alternatywę 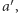tzn. 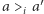dla każdego wyborcy 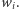Powiemy, że funkcja społecznego dobrobytu 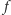spełnia słaby warunek optymalności Pareto, jeśli zawsze w takiej sytuacji zbiorowe uporządkowanie, będące wynikiem zastosowania funkcji 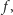spełnia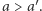

Nietrudno przyznać, że sformułowane powyżej postulaty stanowią rozsądne minimum, konieczne, by uznać funkcję 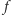za sprawiedliwą.

Badaniem tego typu warunków oraz analizą własności metod podejmowania grupowych decyzji zajmuje się teoria wyboru społecznego. Jej narodziny w latach 50. XX wieku wiązały się z odkryciem serii paradoksów mówiących o tym, że rozsądne, wydawałoby się, warunki, są w praktyce nie do pogodzenia. Bodajże najbardziej znanym tego typu wynikiem jest twierdzenie Arrowa o niemożliwości, pochodzące od amerykańskiego ekonomisty Kennetha Arrowa.

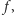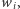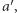Przez dyktaturę rozumiemy funkcję społecznego dobrobytu dla której istnieje taki wyborca że dla każdej pary alternatyw i jeśli 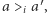to przy podejmowaniu decyzji za pomocą funkcji 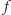grupa uzna alternatywę za lepszą od alternatywy 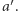Dyktatura spełnia wprawdzie oba sformułowane przez nas wymagania, trudno jednak uznać ją za dobrą metodę podejmowania zbiorowych decyzji. Twierdzenie Arrowa mówi więc w istocie o nieistnieniu funkcji społecznego dobrobytu spełniającej minimalne wymagania sprawiedliwości.

Pozostaje nam udowodnić twierdzenie Arrowa. Przypuśćmy, że grupa 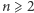osób podejmuje decyzję w sprawie 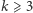alternatyw przy zastosowaniu funkcji społecznego dobrobytu 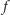spełniającej słaby warunek optymalności Pareto oraz warunek niezależności od alternatyw niezwiązanych. Dla ułatwienia przyjmijmy dodatkowo, że funkcja 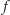jest neutralna. Oznacza to, że każda z alternatyw traktowana jest tak samo. Dokładniej, jeśli każdy wyborca zamieni w swoim uporządkowaniu pewne dwie alternatywy 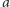i 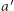miejscami, to w grupowym uporządkowaniu, będącym wynikiem zastosowania funkcji 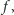alternatywy i 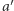również zamienią się miejscami. Założenie to nie jest konieczne, ale uprości nieco dowód przy jednoczesnym zachowaniu jego kluczowych idei.

Grupę wyborców 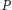nazwiemy decyzyjną w kwestii 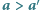, jeśli jest ona w stanie przeforsować decyzję o uznaniu alternatywy 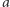za lepszą od 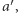tzn. jeśli każda z osób w grupie 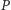przedkłada alternatywę 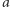nad 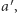natomiast wszyscy pozostali wyborcy przedkładają alternatywę 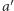nad 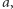to grupową decyzją przy zastosowaniu funkcji 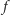jest 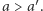Z neutralności funkcji 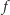wynika, że jeśli grupa 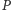jest decyzyjna w kwestii 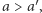to jest ona decyzyjna w kwestii dowolnej innej pary alternatyw. Możemy ją więc nazwać po prostu grupą decyzyjną.

Przez 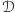oznaczmy zbiór wszystkich grup decyzyjnych. Ponieważ funkcja 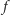spełnia słaby warunek optymalności Pareto, zbiór wszystkich wyborców 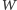jest decyzyjny, czyli należy do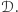

Rozważmy teraz dowolną grupę wyborców 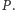Przypuśćmy, że wyborcy w tej grupie przedkładają alternatywę 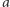nad 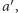zaś wyborcy spoza tej grupy przedkładają alternatywę 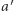nad 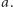Mamy dwie możliwości. Jeśli wspólną decyzją w tej sytuacji jest 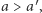to znaczy, że grupa 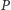jest decyzyjna w kwestii 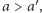czyli po prostu decyzyjna. Jeśli wspólną decyzją jest 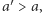to decyzyjna jest grupa 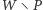(wyborcy należący do 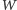i nienależący do 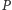). A zatem dokładnie jedna spośród grup 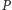oraz 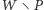należy do zbioru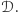

Jeśl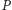i i 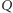są grupami wyborców, to przez 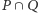oznaczamy zbiór wszystkich tych osób, które należą zarówno do 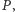jak i do 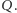Okazuje się, że jeśli grupy 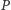i 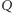są decyzyjne, to grupa 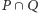również. Rzeczywiście, rozważmy alternatywy 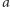oraz 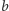i przypuśćmy, że wyborcy w grupie 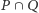uważają alternatywę 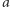za lepszą od 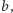natomiast wszyscy pozostali wyborcy mają przeciwne zdanie. 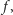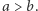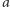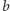Wykażemy, że zbiorowe uporządkowanie, będące wynikiem zastosowania funkcji spełnia Niech będzie alternatywą inną niż i (alternatywa taka istnieje, ponieważ zbiór 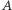ma co najmniej trzy elementy). 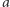Z warunku niezależności od alternatyw niezwiązanych wynika, że preferencje członków grupy wobec alternatywy nie wpływają na grupową decyzję w kwestii alternatyw i 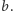Możemy więc założyć, że każdy wyborca w grupie 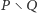ma preferencję 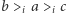; każdy wyborca w grupie 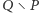uważa, iż 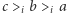; każdy wyborca w grupie 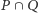jest zdania, że 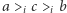; zaś wyborcy spoza grup 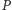i 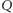uznają porządek 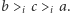Uporządkowania pozostałych alternatyw przyjmijmy dowolne. W wyniku zastosowania funkcji 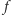otrzymujemy grupowe uporządkowanie alternatyw od najlepszej do najgorszej. Decyzyjność grupy 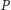implikuje, że w tym uporządkowaniu 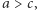zaś decyzyjność grupy 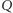implikuje, że 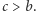Oznacza to, że grupa uznaje alternatywę 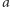za lepszą od 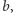co kończy dowód decyzyjności grupy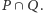

Podsumowując, wykazaliśmy powyżej trzy własności zbioru grup decyzyjnych :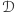

1)

grupa wszystkich wyborców 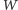należy do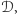

2)

dla każdej grupy wyborców 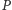dokładnie jedna spośród grup 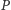oraz 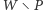należy do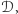

3)

dla każdych dwóch grup 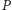i 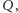należących do 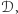grupa 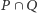należy do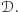

Zbiór spełniający te trzy warunki jest ultrafiltrem podzbiorów zbioru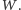

Ostatnim krokiem w dowodzie jest wykazanie, że istnieje taki wyborca 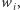iż grupa jest decyzyjna wtedy i tylko wtedy, gdy 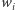jest jej członkiem.

Niech 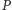będzie grupą osób, które należą do każdej grupy decyzyjnej. Z warunku 3) wynika, że grupa 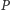jest decyzyjna. Wobec tego grupa 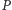nie może być pusta - grupa wszystkich wyborców jest decyzyjna, a zatem warunek 2) implikuje, że grupa pusta nie jest decyzyjna. Niech wyborca 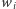należy do grupy 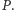Członkowie grupy 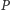z definicji należą do każdej grupy decyzyjnej, czyli w szczególności wyborca 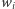należy do każdej grupy decyzyjnej. Z drugiej strony, jeśli 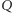jest dowolną grupą, której 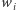jest członkiem, to grupa 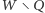nie jest decyzyjna, gdyż 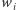do niej nie należy. Z warunku 2) wnioskujemy więc, że grupa 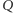jest decyzyjna.

Wyborca 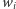jest dyktatorem - jeśli przedkłada on alternatywę 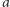nad alternatywę 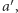to grupa 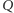osób będących tego samego zdania jest decyzyjna, a zatem przeforsuje ona zbiorową decyzję 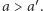To kończy dowód twierdzenia Arrowa.

Wykazaliśmy, że funkcja społecznego dobrobytu niebędąca dyktaturą nie może jednocześnie spełniać słabego warunku optymalności Pareto oraz warunku niezależności od alternatyw niezwiązanych. To i inne tego typu paradoksalne twierdzenia teorii wyboru społecznego sprawiają, że projektowanie grupowych metod podejmowania decyzji jest bardzo skomplikowane. Nieunikniona jest rezygnacja z pewnych pożądanych własności. Spośród postulatów, o których mówi twierdzenie Arrowa, najczęściej porzuca się niezależność od alternatyw niezwiązanych. W praktyce oznacza to, że aby uzyskać bardziej pożądany wynik, czasem opłaca się deklarować preferencje inne niż rzeczywiste. Wybory są więc z konieczności zawsze nie do końca sprawiedliwe.