W co grają kraje, eksploatując środowisko?
4 września 1958 roku islandzki statek patrolowy ICGV Ægir próbował zatrzymać brytyjski kuter rybacki poławiający w strefie 12 mil morskich od brzegów Islandii, został jednak staranowany przez brytyjski okręt wojenny HMS Russell. To był pierwszy incydent pierwszej wojny dorszowej. Co było przyczyną serii konfliktów, w których przeciwko jednej z największych marynarek wojennych Europy stanęła licząca siedem okrętów patrolowych i jeden wodolot flota Islandii? Czego broniła tak zaciekle?

Tytułowa eksploatacja zasobów to nie tylko zagadnienia związane z połowem ryb, ale także m.in. wycinanie lasów tropikalnych, emisja zanieczyszczeń, których nie zatrzymują naniesione na mapę granice, czy eksploatacja transgranicznych złóż ropy. Narzędzia do ich analizy są takie same - gry dynamiczne. Ponieważ te narzędzia są dość złożone, wprowadzimy je stopniowo. Dla ustalenia uwagi omówimy tę klasę zagadnień na przykładzie eksploatacji łowisk. Zaczniemy od definicji gry.
Gra jest to dowolna sytuacja podejmowania decyzji przez co najmniej dwóch decydentów (graczy), w której każdy działa we własnym celu (wyrażonym jako maksymalizacja funkcji wypłaty), ale na realizację celu przez gracza mają wpływ decyzje podjęte przez pozostałych (funkcje wypłaty graczy zależą od całego układu strategii).
Równowaga Nasha to taki układ strategii, że żaden z graczy nie może zwiększyć wypłaty przez zmianę strategii przy niezmienionych strategiach pozostałych. A więc równowaga Nasha to taki układ strategii, w którym żaden z graczy nie żałuje swojej decyzji, znając wybory innych.
Przykład 1. Pięciu rybaków z Jastarni, posiadających po 2 kutry, sprzedaje swój połów na wspólnym targu. Każdy użyty kuter wyławia 1 tonę śledzia. Cena, po której mogą sprzedać ryby, to 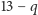 za tonę, gdzie
za tonę, gdzie 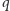 to łączna liczba wyłowionych ton ryb. Koszt pracy każdego statku wynosi 1. Zysk gracza
to łączna liczba wyłowionych ton ryb. Koszt pracy każdego statku wynosi 1. Zysk gracza 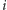 to zatem
to zatem

gdzie 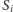 - liczba jego kutrów wysłanych na połów.
- liczba jego kutrów wysłanych na połów.
Zauważmy, że najlepsza odpowiedź każdego z graczy na strategie pozostałych to zawsze 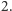 Tak więc jedyną równowagą Nasha jest układ strategii
Tak więc jedyną równowagą Nasha jest układ strategii 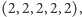 w którym każdy z graczy dostaje wypłatę
w którym każdy z graczy dostaje wypłatę 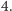 Co by było, gdyby ograniczyli się i każdy wysłał po jednym statku? Wtedy każdy dostałby wypłatę
Co by było, gdyby ograniczyli się i każdy wysłał po jednym statku? Wtedy każdy dostałby wypłatę 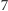 ! Wszyscy by skorzystali na takim porozumieniu. Jednak każdy z graczy jeszcze bardziej skorzystałby na wysłaniu dwóch statków, kiedy pozostali uczciwie trzymają się umowy (wtedy on dostałby 12, a pozostali po 6). To właśnie jest istota tragedii wspólnych zasobów (the tragedy of the commons) w najprostszym ujęciu (na razie wspólny jest jedynie rynek). Jak widać, "magiczna ręka rynku" w zagadnieniach wspólnych zasobów nie działa.
! Wszyscy by skorzystali na takim porozumieniu. Jednak każdy z graczy jeszcze bardziej skorzystałby na wysłaniu dwóch statków, kiedy pozostali uczciwie trzymają się umowy (wtedy on dostałby 12, a pozostali po 6). To właśnie jest istota tragedii wspólnych zasobów (the tragedy of the commons) w najprostszym ujęciu (na razie wspólny jest jedynie rynek). Jak widać, "magiczna ręka rynku" w zagadnieniach wspólnych zasobów nie działa.
Jak wymusić kooperację?
1. Wiążące ograniczenia. Komisyjnie zamykamy po jednym statku każdego z graczy w porcie. W porównaniu z równowagą Nasha jest to lepsze dla wszystkich.
2. Podatek regulacyjny. Podatków nikt nie lubi. Jednak podatek czysto regulacyjny, płacony od przekroczenia zawartego w umowie limitu, jeśli umiejętnie obliczony (w naszym przypadku większy niż 5), nie jest płacony przez nikogo, a na pewno zadziała.
3. Pozwolenia zbywalne. Ustalamy limit statków na 5 i rozdzielamy go równo pomiędzy graczy. Każdy może łowić w ramach posiadanych pozwoleń, którymi gracze mogą swobodnie handlować między sobą. Cenę pozwolenia wyznacza rynek.
Gry dynamiczne. Czego brakuje w tej analizie? Każdego dnia gracze mogą rozpocząć kolejną taką samą prostą grę. Być może dobrze opisywałaby ona rybołówstwo morskie w średniowieczu, ale nie przy obecnych możliwościach technicznych - nadmiernie poławianych ryb będzie coraz mniej, a w skrajnym przypadku mogą nawet wyginąć. Przyczyną wojen dorszowych było właśnie istotne zmniejszenie populacji łowisk.
Do pełniejszego opisu zjawiska potrzebujemy kolejnych punktów w czasie i nowej zmiennej - zmiennej stanu, oznaczającej liczbę lub biomasę ryb w łowisku. Strategie graczy opisują, co gracz zrobi w każdym momencie gry, ewentualnie w zależności od stanu łowiska. Gracze biorą pod uwagę nie tylko bieżącą wypłatę, ale całkowity zysk (również przyszły) przy uwzględnieniu, że jedna złotówka zarobiona w przyszłości może mieć inną wartość - tzw. dyskonto.
Przykład 2. O ile pięciu rybaków z Jastarni nie może zagrozić populacji bałtyckiego śledzia, to pięć nadbałtyckich krajów już tak. Teraz graczami są kraje, a gra z przykładu 1 (oczywiście z nieco innymi jednostkami) toczy się przez dwa okresy, czynnikiem dyskontowym jest 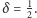 Jeśli łączna eksploatacja przekroczy 5, stan populacji ryb zmniejsza się z
Jeśli łączna eksploatacja przekroczy 5, stan populacji ryb zmniejsza się z 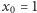 (populacja w niskim, ale stabilnym stanie) do
(populacja w niskim, ale stabilnym stanie) do 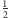 (populacja mocno przetrzebiona), a jeśli natomiast łączna eksploatacja przekroczy 7, to stan zmniejsza się do pewnego małego
(populacja mocno przetrzebiona), a jeśli natomiast łączna eksploatacja przekroczy 7, to stan zmniejsza się do pewnego małego 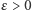 (populacja na skraju wyginięcia). Przy stanie
(populacja na skraju wyginięcia). Przy stanie 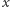 każdy statek może złowić maksymalnie
każdy statek może złowić maksymalnie 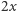 jednostek ryb, ponadto koszty rosną
jednostek ryb, ponadto koszty rosną 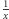 razy. Przyjmujemy
razy. Przyjmujemy  na tyle małe, że w tym stanie połowy stają się nieopłacalne. W tej grze, podobnie jak w przykładzie 1, w jedynej równowadze Nasha gracze łowią z maksymalną intensywnością w okresie początkowym, doprowadzając populację śledzia na skraj wyginięcia, mimo że oznacza to dla nich głodowanie w okresie 1. Wypłata każdego z graczy jest równa 4, podczas gdy w razie porozumienia każdy mógłby mieć 10, 5.
na tyle małe, że w tym stanie połowy stają się nieopłacalne. W tej grze, podobnie jak w przykładzie 1, w jedynej równowadze Nasha gracze łowią z maksymalną intensywnością w okresie początkowym, doprowadzając populację śledzia na skraj wyginięcia, mimo że oznacza to dla nich głodowanie w okresie 1. Wypłata każdego z graczy jest równa 4, podczas gdy w razie porozumienia każdy mógłby mieć 10, 5.
W grach dynamicznych eksploatacji zasobów można stosować te same metody  wymuszania kooperacji, możliwe są też inne, specyficzne metody oparte na fakcie wielokrotnego wchodzenia w interakcję (np. porozumienia międzynarodowe, w których jedyną sankcją za wyłamanie się gracza z kooperacji jest groźba zerwania porozumienia i powrót do nieopłacalnej dla wszystkich równowagi Nasha).
wymuszania kooperacji, możliwe są też inne, specyficzne metody oparte na fakcie wielokrotnego wchodzenia w interakcję (np. porozumienia międzynarodowe, w których jedyną sankcją za wyłamanie się gracza z kooperacji jest groźba zerwania porozumienia i powrót do nieopłacalnej dla wszystkich równowagi Nasha).
Pierwsze modele gier dynamicznych opisujących eksploatację środowiska były zainspirowane wspomnianymi wojnami dorszowymi, które zakończyły się wydzieleniem 200-milowej wyłącznej strefy ekonomicznej Islandii, co dziś jest już standardem gwarantowanym prawem międzynarodowym. Warto jednak zauważyć, że taka "prywatyzacja" łowisk nie rozwiązuje w całości problemu, ponieważ formalne granice stref ekonomicznych są ignorowane przez ryby, które mogą przepływać tam, gdzie jest ich mniejsze zagęszczenie, a więc więcej pokarmu. Powoduje to, że każdemu z krajów opłaca się do pewnego poziomu zwiększać eksploatację w swojej strefie, zwłaszcza jeśli pozostali postanowili ograniczyć eksploatację w swoich. Zagadnienie to staje się znacznie bardziej złożone, bo już sam fakt istnienia specjalnych stref ekonomicznych wymaga użycia wielowymiarowej zmiennej stanu i wzięcia pod uwagę opóźnienia, ponadto w morzach mamy więcej niż jeden gatunek ryb, a na szybkość rozmnażania się oprócz biomasy ma wpływ struktura wiekowa populacji... Widać więc, że nawet liczenie jedynie równowag Nasha w grach eksploatacji zasobów morskich, nie wspominając nawet o konstrukcji porozumień międzynarodowych, dzięki którym uda się wymusić kooperację, oznacza zajęcie dla matematyków na długie lata.
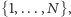 ich strategie
ich strategie 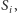 funkcje wypłat
funkcje wypłat 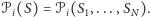
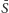 dla każdego gracza
dla każdego gracza 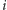 i każdej jego strategii
i każdej jego strategii