Co to jest?
Opcje i greckie parametry
Opcje są kontraktami, które posiadaczowi dają prawo (ale nie obowiązek) zakupu (lub sprzedaży) określonego towaru w ustalonej chwili w przyszłości (termin realizacji) po ustalonej cenie (cena realizacji). Opcja jest więc umową, która jednej stronie (posiadaczowi) daje pewne prawa, które muszą być realizowane przez drugą stronę umowy (sprzedawcę opcji). Oczywiście, za uzyskane prawa posiadacz opcji musi zapłacić sprzedawcy określoną cenę.
Zasadniczym problemem przy kontraktach opcyjnych jest właściwa wycena takiego kontraktu. Przy braku odpowiedniego aparatu matematycznego robiono to intuicyjnie, co często prowadziło do znacznych błędów. Dopiero pod koniec XIX wieku zaczęto rozumieć czynniki, które wpływają na cenę opcji. Ważnym krokiem była praca L. Bacheliera z 1900 roku, w której ceny towaru, na który wystawiana jest opcja, były modelowane procesami stochastycznymi. Jednak dopiero w zaproponowanym w 1973 roku modelu F. Blacka i M. Scholesa znaleziono poprawny sposób wyceny opcji.
Model Blacka-Scholesa pozwala w postaci analitycznego wzoru zapisać cenę towaru, na który wystawiana jest opcja:

We wzorze tym za losowe zachowanie cen odpowiada proces Wienera 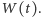
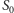 jest ceną w chwili
jest ceną w chwili 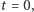 parametr
parametr  opisuje obowiązującą na rynku stopę procentową, a
opisuje obowiązującą na rynku stopę procentową, a 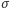 jest "zmiennością" ceny (duże
jest "zmiennością" ceny (duże 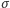 odpowiada dużym fluktuacjom ceny). Kiedy znana jest cena towaru (instrumentu bazowego), to korzystając z odpowiedniego aparatu matematycznego, można obliczyć cenę opcji.
odpowiada dużym fluktuacjom ceny). Kiedy znana jest cena towaru (instrumentu bazowego), to korzystając z odpowiedniego aparatu matematycznego, można obliczyć cenę opcji.
Na współczesnym rynku finansowym interesuje nas nie tylko cena opcji 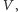 ale także tzw. greckie parametry, które są niczym innym jak pochodnymi ceny opcji po zmiennych, od których ta cena zależy. Mamy więc parametry:
ale także tzw. greckie parametry, które są niczym innym jak pochodnymi ceny opcji po zmiennych, od których ta cena zależy. Mamy więc parametry:

oraz kilka innych. Greckie parametry pełnią ważną funkcję na rynku finansowym, ponieważ są one wykorzystywane do zmniejszania ryzyka inwestycji w opcje.
Analityczny wzór na cenę instrumentu bazowego można wyprowadzić tylko dla bardzo uproszczonego modelu rynku. Podany wyżej wzór zakładał, że  i
i 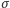 są stałe. Mając taki wzór, można wyprowadzić także analityczny wzór na cenę opcji oraz greckie parametry. Modele takie są jednak zbyt uproszczonymi modelami rzeczywistego rynku. W bardziej zaawansowanych modelach przyjmuje się, że zmienność
są stałe. Mając taki wzór, można wyprowadzić także analityczny wzór na cenę opcji oraz greckie parametry. Modele takie są jednak zbyt uproszczonymi modelami rzeczywistego rynku. W bardziej zaawansowanych modelach przyjmuje się, że zmienność 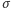 jest funkcją ceny instrumentu bazowego
jest funkcją ceny instrumentu bazowego 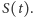 W takich modelach nie daje się już zwykle wyprowadzić wzoru na cenę instrumentu bazowego. Wtedy do wyceny opcji oraz obliczenia jej greckich parametrów musimy wykorzystać metody numeryczne.
W takich modelach nie daje się już zwykle wyprowadzić wzoru na cenę instrumentu bazowego. Wtedy do wyceny opcji oraz obliczenia jej greckich parametrów musimy wykorzystać metody numeryczne.
Jednym z najprostszych numerycznych algorytmów obliczania cen opcji jest algorytm drzewa dwumianowego. W modelu dwumianowym czas 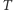 do zapadalności opcji dzielimy na
do zapadalności opcji dzielimy na 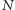 okresów o długości
okresów o długości 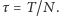 Drzewo dwumianowe konstruowane jest dla momentów czasu
Drzewo dwumianowe konstruowane jest dla momentów czasu 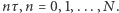 Jeśli
Jeśli 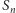 oznacza cenę instrumentu bazowego w węźle
oznacza cenę instrumentu bazowego w węźle 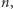 to cena w węźle
to cena w węźle 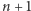 dana jest wzorem
dana jest wzorem 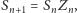 gdzie
gdzie 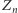 są niezależnymi zmiennymi losowymi o jednakowym rozkładzie dwupunktowym
są niezależnymi zmiennymi losowymi o jednakowym rozkładzie dwupunktowym

a 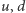 i
i 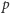 są dane, przy czym
są dane, przy czym 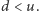
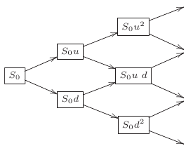
Rys. 1 Drzewo dwumianowe
Ponieważ 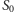 jest znane, otrzymujemy drzewo dwumianowe pokazane na rysunku 1 Aby obliczyć na tym drzewie cenę opcji, należy prawdopodobieństwo
jest znane, otrzymujemy drzewo dwumianowe pokazane na rysunku 1 Aby obliczyć na tym drzewie cenę opcji, należy prawdopodobieństwo 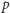 w definicji zmiennej
w definicji zmiennej 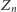 zamienić na
zamienić na 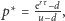 które jest prawdopodobieństwem neutralnym względem ryzyka. Mając wyznaczone prawdopodobieństwo
które jest prawdopodobieństwem neutralnym względem ryzyka. Mając wyznaczone prawdopodobieństwo 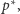 można szybko obliczyć cenę opcji. Dla opcji kupna z ceną
można szybko obliczyć cenę opcji. Dla opcji kupna z ceną 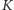 i terminem zapadalności
i terminem zapadalności 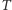 cena ta liczona jest "wstecz" na drzewie dwumianowym. Zauważmy w tym celu, że ceny instrumentu bazowego w węzłach odpowiadających czasowi zapadalności
cena ta liczona jest "wstecz" na drzewie dwumianowym. Zauważmy w tym celu, że ceny instrumentu bazowego w węzłach odpowiadających czasowi zapadalności 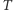 mają postać
mają postać 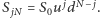 Niech
Niech 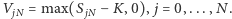 Wtedy, cofając się po węzłach drzewa od węzła
Wtedy, cofając się po węzłach drzewa od węzła 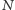 do węzła
do węzła 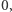 korzystamy ze wzoru
korzystamy ze wzoru

Obliczona z tego algorytmu wartość 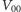 jest poszukiwaną ceną opcji.
jest poszukiwaną ceną opcji.
Aby zilustrować działanie algorytmu drzewa dwumianowego, rozważmy model zwany modelem CEV, w którym 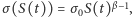 gdzie
gdzie 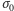 jest stałą. W modelu tym nie można wyprowadzić analitycznego wzoru na
jest stałą. W modelu tym nie można wyprowadzić analitycznego wzoru na 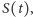 ale można wyprowadzić analityczny wzór na gęstość tego procesu. Niestety, wzór ten zawiera skomplikowaną całkę, którą należy obliczać numerycznie. Prostsze jest bezpośrednie numeryczne obliczenie ceny opcji. Konstrukcja drzewa dwumianowego wymaga ustalenia wartości
ale można wyprowadzić analityczny wzór na gęstość tego procesu. Niestety, wzór ten zawiera skomplikowaną całkę, którą należy obliczać numerycznie. Prostsze jest bezpośrednie numeryczne obliczenie ceny opcji. Konstrukcja drzewa dwumianowego wymaga ustalenia wartości 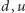 oraz
oraz 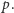 Obliczamy je z danych uzyskanych z obserwacji zachowania się cen instrumentu bazowego na rzeczywistym rynku. W modelu CEV wzory są nieco bardziej skomplikowane niż w modelu Blacka-Scholesa i podobnie jak dla tego ostatniego modelu nie będziemy ich tutaj przedstawiali. Kiedy znamy już wartości
Obliczamy je z danych uzyskanych z obserwacji zachowania się cen instrumentu bazowego na rzeczywistym rynku. W modelu CEV wzory są nieco bardziej skomplikowane niż w modelu Blacka-Scholesa i podobnie jak dla tego ostatniego modelu nie będziemy ich tutaj przedstawiali. Kiedy znamy już wartości 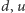 i
i 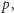 to obliczenie ceny opcji (oraz jej greckich parametrów) wymaga ustalenia właściwej liczby węzłów
to obliczenie ceny opcji (oraz jej greckich parametrów) wymaga ustalenia właściwej liczby węzłów 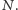 Pozornie zadanie wydaje się łatwe - należy wybrać wielkość
Pozornie zadanie wydaje się łatwe - należy wybrać wielkość 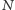 tak, aby uzyskać cenę opcji z wymaganą dokładnością. Zobaczmy, jak wygląda cena opcji w modelu CEV dla różnej liczby węzłów
tak, aby uzyskać cenę opcji z wymaganą dokładnością. Zobaczmy, jak wygląda cena opcji w modelu CEV dla różnej liczby węzłów  (patrz Rys. 2).
(patrz Rys. 2).
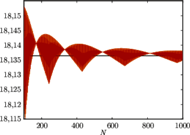
Rys. 2 Cena opcji - drzewo dwumianowe
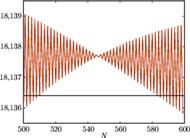
Rys. 2a Cena opcji - drzewo dwumianowe
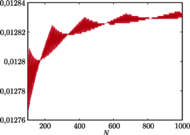
Rys. 3 Wartość parametru 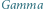 - drzewo dwumianowe
- drzewo dwumianowe
Obraz na rysunku 2 jest dość zaskakujący. Spodziewaliśmy się obrazu krzywej, która każdej wartości 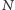 przypisuje cenę opcji. Tymczasem dostaliśmy jakieś "dziwne precle". Dla zrozumienia, co naprawdę pokazuje rysunek 2, powiększmy jego fragment. Ten powiększony fragment jest pokazany na rysunku 2a (pozioma linia na obu rysunkach to dokładna cena opcji, którą otrzymaliśmy, obliczając numerycznie wspomnianą wcześniej całkę opisującą gęstość procesu
przypisuje cenę opcji. Tymczasem dostaliśmy jakieś "dziwne precle". Dla zrozumienia, co naprawdę pokazuje rysunek 2, powiększmy jego fragment. Ten powiększony fragment jest pokazany na rysunku 2a (pozioma linia na obu rysunkach to dokładna cena opcji, którą otrzymaliśmy, obliczając numerycznie wspomnianą wcześniej całkę opisującą gęstość procesu 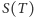 ). Teraz już widać, że dostaliśmy wykres, który każdej wartości
). Teraz już widać, że dostaliśmy wykres, który każdej wartości 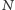 przypisuje jedną cenę opcji. Problem polega na tym, że ten wykres oscyluje między dwiema skrajnymi wartościami (obwiedniami). Podobnie wygląda obliczenie greckich parametrów. Rysunek 3 pokazuje wyniki obliczenia jednego z tych parametrów
przypisuje jedną cenę opcji. Problem polega na tym, że ten wykres oscyluje między dwiema skrajnymi wartościami (obwiedniami). Podobnie wygląda obliczenie greckich parametrów. Rysunek 3 pokazuje wyniki obliczenia jednego z tych parametrów 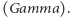 Widać z tych rysunków, że obliczenie ceny opcji albo jej greckich parametrów dla jednej wartości
Widać z tych rysunków, że obliczenie ceny opcji albo jej greckich parametrów dla jednej wartości 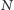 daje nam mało precyzyjną informację (nie wiemy, w jakim fragmencie oscylującej krzywej wylądowaliśmy). Optymistyczna informacja, jaka wynika z rysunków 2 i 3, jest taka, że przy wzroście
daje nam mało precyzyjną informację (nie wiemy, w jakim fragmencie oscylującej krzywej wylądowaliśmy). Optymistyczna informacja, jaka wynika z rysunków 2 i 3, jest taka, że przy wzroście 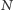 oscylacje mają zmniejszającą się amplitudę. Jeśli więc dokonamy obliczeń dla wielu wartości
oscylacje mają zmniejszającą się amplitudę. Jeśli więc dokonamy obliczeń dla wielu wartości 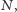 to będziemy znali położenie górnej i dolnej obwiedni oscylacji. Będziemy mogli wtedy wybrać takie
to będziemy znali położenie górnej i dolnej obwiedni oscylacji. Będziemy mogli wtedy wybrać takie 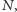 dla którego amplituda oscylacji będzie mniejsza niż oczekiwana dokładność obliczenia ceny opcji albo jej greckich parametrów.
dla którego amplituda oscylacji będzie mniejsza niż oczekiwana dokładność obliczenia ceny opcji albo jej greckich parametrów.
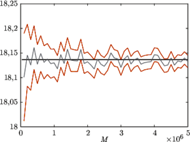
Rys. 4 Cena opcji - metoda Monte Carlo
Czytelnik mógłby pomyśleć, że otrzymane na rysunkach 2 i 3 oscylacje to cecha użytej metody numerycznej, a inne metody będą dawały wyniki pozbawione takich mankamentów. Spróbujmy więc obliczyć cenę opcji, wykorzystując metodę Monte Carlo. W metodzie tej dokonując losowań z odpowiedniego rozkładu, możemy symulować trajektorie procesu 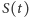 i wyznaczyć wartości końcowe
i wyznaczyć wartości końcowe 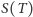 na każdej trajektorii. Symulując dostatecznie dużo trajektorii, możemy wartość oczekiwaną w podanym na marginesie wzorze
na każdej trajektorii. Symulując dostatecznie dużo trajektorii, możemy wartość oczekiwaną w podanym na marginesie wzorze 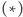 na cenę opcji zastąpić średnią po trajektoriach (pozwala na to prawo wielkich liczb). Prócz obliczenia średniej możemy także obliczyć średni błąd, który jest dobrym przybliżeniem wariancji zmiennej losowej
na cenę opcji zastąpić średnią po trajektoriach (pozwala na to prawo wielkich liczb). Prócz obliczenia średniej możemy także obliczyć średni błąd, który jest dobrym przybliżeniem wariancji zmiennej losowej 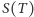 i pozwala wyznaczyć przedział ufności dla średniej. Wyniki takich obliczeń dla bardzo dużej liczby symulacji (do
i pozwala wyznaczyć przedział ufności dla średniej. Wyniki takich obliczeń dla bardzo dużej liczby symulacji (do 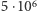 ) pokazane są na rysunku 4 Zaznaczono na tym rysunku średnią oraz górną i dolną granicę przedziału ufności dla poziomu ufności 95% (to oznacza, że z prawdopodobieństwem 0,95 poprawny wynik leży w tym przedziale). Niestety, także dla metody Monte Carlo dostaliśmy oscylujący wykres. Oscylacje są, oczywiście, mniej gwałtowne niż dla drzewa dwumianowego. Ale to jest częściowo spowodowane faktem, że obliczenia robiliśmy dla kolejnych wartości
) pokazane są na rysunku 4 Zaznaczono na tym rysunku średnią oraz górną i dolną granicę przedziału ufności dla poziomu ufności 95% (to oznacza, że z prawdopodobieństwem 0,95 poprawny wynik leży w tym przedziale). Niestety, także dla metody Monte Carlo dostaliśmy oscylujący wykres. Oscylacje są, oczywiście, mniej gwałtowne niż dla drzewa dwumianowego. Ale to jest częściowo spowodowane faktem, że obliczenia robiliśmy dla kolejnych wartości 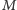 odległych od siebie. Gdyby obliczenia na drzewie dwumianowym robić dla oddalonych od siebie wartości
odległych od siebie. Gdyby obliczenia na drzewie dwumianowym robić dla oddalonych od siebie wartości 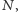 to obraz byłby podobny jak na rysunku 4
to obraz byłby podobny jak na rysunku 4
Dokładna wycena instrumentów finansowych nie jest więc sprawą prostą. Nawet jeśli wiemy, jakie pułapki na nas czyhają, musimy wykonać wiele obliczeń (dla różnych wartości 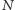 lub
lub 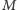 ), aby oszacować błąd otrzymanego rozwiązania. Wiedza, czyli znajomość pułapek, może nas jednak ustrzec przed wyciągnięciem zbyt optymistycznych wniosków z wyników uzyskanych dla małej liczby symulacji.
), aby oszacować błąd otrzymanego rozwiązania. Wiedza, czyli znajomość pułapek, może nas jednak ustrzec przed wyciągnięciem zbyt optymistycznych wniosków z wyników uzyskanych dla małej liczby symulacji.
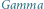 - drzewo dwumianowe
- drzewo dwumianowe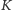 w momencie
w momencie 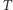 ) ma postać
) ma postać![E[exp( −rT )max(S(T )− K, 0)].](/math/temat/matematyka/zastosowania/2017/07/29/Opcje_i_greckie_parametry/3x-697bd6654c5214744623e164c39be9ab81d0ee79-dm-33,33,33-FF,FF,FF.gif)