Z życia managera magazynu, czyli jak składać optymalne zamówienia?
Spróbuj, drogi Czytelniku, wyobrazić sobie, że zarządzasz wielkim magazynem z milionami różnych towarów na półkach. W Twoim magazynie znajdują się części zamiennie do koparek, samochodów i motocykli, śrubki, silniki, narzędzia, odzież specjalistyczna, smary i oleje napędowe, oraz inne motoryzacyjne cuda. Jeżeli wczułeś się już w swoją rolę, pozwól, że zadam Ci pytanie. W jaki sposób zarządzasz towarami? Skąd wiesz, kiedy złożyć zamówienie?

Czy masz ustalony grafik i zamawiasz na początku każdego miesiąca, mimo tego, że niektóre części piętrzą się aż po sufit? A może zamawiasz dopiero wtedy, gdy zabraknie Ci towaru na półce? A co, jeżeli dostawa trwa dwa miesiące, a przed drzwiami magazynu rozentuzjazmowany tłum harleyowców domaga się nowego modelu skórzanych kurtek? Być może, zamawiasz, gdy ilość towaru jest odpowiednio mała? Ale co to znaczy odpowiednio mała? Czy 5 śrubek to wystarczająco mało? A 5 silników do supernowoczesnego, rzadkiego modelu koparki? Poszukiwanie odpowiedzi na podobne pytania to codzienność w Syncronie - moim miejscu pracy. Nasz główny produkt jest aplikacją, dzięki której sieć magazynów może zaoszczędzić pieniądze poprzez m.in. minimalizację ilości przechowywanych towarów, optymalizację procesu składania zamówień i efektywne zarządzanie łańcuchem dostaw. W niniejszym artykule opowiem o małym wycinku jednej z funkcjonalności, to znaczy o strategii zamawiania 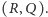 Zasada działania tej strategii jest bardzo prosta - składasz zamówienie o wielkości
Zasada działania tej strategii jest bardzo prosta - składasz zamówienie o wielkości 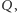 kiedy zauważysz, że ilość towaru spadnie do poziomu
kiedy zauważysz, że ilość towaru spadnie do poziomu 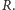
Ile zamawiać?
Teoretyczne opracowania na temat strategii 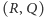 nie określają jasno, ile zamawiać. Ważne jest natomiast, aby wielkość zamówienia nie zmieniała się istotnie w czasie. Przy wyborze odpowiedniego
nie określają jasno, ile zamawiać. Ważne jest natomiast, aby wielkość zamówienia nie zmieniała się istotnie w czasie. Przy wyborze odpowiedniego 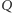 możemy kierować się minimalizacją istotnych kosztów, np. kosztów zamawiania (transport, rozładunek) i przechowywania (koszty związane z zamrożeniem kapitału, składowaniem, potencjalnym zniszczeniem towaru). W praktyce precyzyjne oszacowanie poszczególnych kosztów jest skomplikowane, dlatego też w ramach alternatywy możemy zastosować nieco prostszą formułę,
możemy kierować się minimalizacją istotnych kosztów, np. kosztów zamawiania (transport, rozładunek) i przechowywania (koszty związane z zamrożeniem kapitału, składowaniem, potencjalnym zniszczeniem towaru). W praktyce precyzyjne oszacowanie poszczególnych kosztów jest skomplikowane, dlatego też w ramach alternatywy możemy zastosować nieco prostszą formułę, 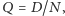 gdzie
gdzie 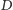 to oczekiwany roczny popyt, a
to oczekiwany roczny popyt, a 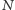 to planowana liczba zamówień w roku.
to planowana liczba zamówień w roku.
Kiedy zamawiać?
Przyjmijmy na początek, że popyt i czas dostawy są deterministyczne. Przy znanym popycie możemy dokładnie przewidzieć, kiedy sprzedamy wszystko to, co mamy obecnie w magazynie. Ponieważ czas dostawy jest ustalony, możemy złożyć zamówienie odpowiednio wcześniej - na tyle wcześnie, aby dostawa wypadła w dniu, gdy klient kupuje ostatnią sztukę towaru. Formalizując nieco te rozmyślania,

W rzeczywistości popyt nie jest deterministyczny, dlatego też porzucamy to założenie. Dla ustalenia uwagi przyjmujemy, że mamy do czynienia ze zmienną losową o rozkładzie normalnym 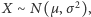 gdzie
gdzie 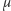 to oczekiwany popyt w czasie oczekiwania na dostawę, a
to oczekiwany popyt w czasie oczekiwania na dostawę, a 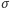 to niepewność naszej prognozy. Podobnie jak poprzednio, moglibyśmy złożyć zamówienie w momencie, gdy ilość towaru w magazynie jest równa
to niepewność naszej prognozy. Podobnie jak poprzednio, moglibyśmy złożyć zamówienie w momencie, gdy ilość towaru w magazynie jest równa 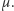 Zauważmy jednak, że takie postępowanie daje nam tylko 50% szans, że wszyscy klienci zostaną obsłużeni (rozkład normalny jest symetryczny względem średniej). Ta niepewność prognozy sprawia, że powinniśmy mieć dodatkową pulę towaru na "wszelki wypadek", czyli, innymi słowy, złożyć zamówienie nieco wcześniej. Czy dużo wcześniej? To zależy od poziomu obsługi, który chcemy zapewnić naszym klientom. Pozwólcie, że na moment zboczę nieco z tematu i wtrącę kilka słów o miarach poziomu obsługi, których najczęściej używa się w praktyce.
Zauważmy jednak, że takie postępowanie daje nam tylko 50% szans, że wszyscy klienci zostaną obsłużeni (rozkład normalny jest symetryczny względem średniej). Ta niepewność prognozy sprawia, że powinniśmy mieć dodatkową pulę towaru na "wszelki wypadek", czyli, innymi słowy, złożyć zamówienie nieco wcześniej. Czy dużo wcześniej? To zależy od poziomu obsługi, który chcemy zapewnić naszym klientom. Pozwólcie, że na moment zboczę nieco z tematu i wtrącę kilka słów o miarach poziomu obsługi, których najczęściej używa się w praktyce.
- CSL (ang. Cycle Service Level) - prawdopodobieństwo zaspokojenia całego popytu w okresie pomiędzy dostawami wyrażone w procentach,
- IFR (ang. Item Fill Rate) - procent zaspokojonego popytu,
- OFR (ang. Order Fill Rate) - procent zamówień zrealizowanych w całości.
Aby doświadczyć różnicy pomiędzy powyższymi miarami, rozważmy scenariusz, w którym zamówienie o wielkości 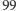 dostarczane jest regularnie pierwszego dnia miesiąca. Popyt jest stały i wynosi
dostarczane jest regularnie pierwszego dnia miesiąca. Popyt jest stały i wynosi 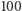 sztuk miesięcznie. Oczywiste jest, że
sztuk miesięcznie. Oczywiste jest, że 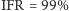 i
i 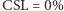 (bo w każdym okresie zabraknie jednej sztuki). OFR zależy od charakterystyki popytu. Jeżeli jeden klient zamówił 100 sztuk, to
(bo w każdym okresie zabraknie jednej sztuki). OFR zależy od charakterystyki popytu. Jeżeli jeden klient zamówił 100 sztuk, to 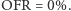 Jeżeli dwóch klientów złożyło po jednym zamówieniu na 50 sztuk, to
Jeżeli dwóch klientów złożyło po jednym zamówieniu na 50 sztuk, to 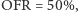 ponieważ tylko jedno z dwóch zamówień zostało w całości zrealizowane.
ponieważ tylko jedno z dwóch zamówień zostało w całości zrealizowane.
Wróćmy do ustalenia satysfakcjonującej wartości 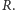 Załóżmy, że chcemy zapewnić poziom obsługi CSL równy
Załóżmy, że chcemy zapewnić poziom obsługi CSL równy 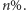 Szukamy zatem takiego
Szukamy zatem takiego 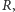 że popyt w czasie oczekiwania na dostawę nie przekroczy tej wartości z prawdopodobieństwem
że popyt w czasie oczekiwania na dostawę nie przekroczy tej wartości z prawdopodobieństwem 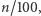 czyli
czyli

Znając rozkład zmiennej losowej 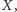 łatwo znajdujemy odpowiednią wartość
łatwo znajdujemy odpowiednią wartość 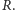 Trochę więcej gimnastyki wymaga wyznaczenie
Trochę więcej gimnastyki wymaga wyznaczenie 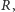 które zapewni z góry zadany poziom IFR. Zgodnie z definicją,
które zapewni z góry zadany poziom IFR. Zgodnie z definicją,

Jednak w praktyce stosuje się dosyć dobre przybliżenie, z którym łatwiej pracować

my w dalszej części będziemy stosować ten właśnie wzór.
Oczekiwany popyt w okresie pomiędzy zamówieniami jest równy 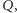 a wartość oczekiwana niezaspokojonego popytu zależy od
a wartość oczekiwana niezaspokojonego popytu zależy od 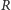 i jest modelowana przez funkcję straty
i jest modelowana przez funkcję straty

gdzie 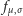 oznacza gęstość rozkładu normalnego o średniej
oznacza gęstość rozkładu normalnego o średniej 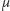 i odchyleniu standardowym
i odchyleniu standardowym 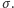 Przy odrobinie cierpliwości można wykazać, że funkcja
Przy odrobinie cierpliwości można wykazać, że funkcja 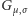 jest ściśle malejąca, istnieje zatem funkcja do niej odwrotna, dzięki czemu
jest ściśle malejąca, istnieje zatem funkcja do niej odwrotna, dzięki czemu 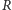 może być jednoznacznie wyznaczone. Odpowiednia wartość
może być jednoznacznie wyznaczone. Odpowiednia wartość 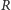 uzyskiwana jest numerycznie. Dużym ułatwieniem przy obliczeniach jest standaryzacja rozkładu, która prowadzi do zależności
uzyskiwana jest numerycznie. Dużym ułatwieniem przy obliczeniach jest standaryzacja rozkładu, która prowadzi do zależności

oraz formuła 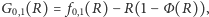 którą można otrzymać z wyjściowego wzoru (
którą można otrzymać z wyjściowego wzoru ( 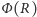 to dystrybuanta rozkładu
to dystrybuanta rozkładu 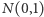 ).
).
Przykład. Załóżmy, że popyt w czasie oczekiwania na dostawę modelowany jest rozkładem normalnym o średniej 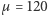 i odchyleniu standardowym
i odchyleniu standardowym 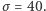 Czas oczekiwania na dostawę wynosi
Czas oczekiwania na dostawę wynosi 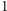 tydzień, a zamówienie składane jest
tydzień, a zamówienie składane jest 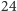 razy w roku. Naszym zadaniem jest wyznaczenie strategii
razy w roku. Naszym zadaniem jest wyznaczenie strategii 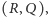 która zapewni
która zapewni 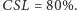 Jaki jest oczekiwany poziom IFR dla takiej strategii? Obliczmy najpierw wielkość zamówienia:
Jaki jest oczekiwany poziom IFR dla takiej strategii? Obliczmy najpierw wielkość zamówienia:

Zgodnie z definicją CSL szukamy kwantyla rzędu 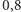 dla zmiennej losowej
dla zmiennej losowej 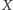 o rozkładzie
o rozkładzie 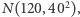 tzn. takiej wartości
tzn. takiej wartości 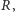 że
że 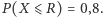 Korzystając z tablic lub dowolnego pakietu statystycznego, otrzymujemy
Korzystając z tablic lub dowolnego pakietu statystycznego, otrzymujemy

Szukana strategia to 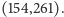 Teraz sprawdźmy, jaki jest oczekiwany IFR dla wyliczonej strategii
Teraz sprawdźmy, jaki jest oczekiwany IFR dla wyliczonej strategii
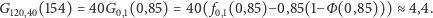 |
A zatem,


W niniejszym artykule przyjęliśmy kilka założeń ułatwiających zrozumienie badanego procesu i ułatwiających same obliczenia, np. popyt nie zawsze może być modelowany rozkładem normalnym. W przypadku towarów, które sprzedają się rzadko i w nieregularny sposób, konieczne jest użycie rozkładów dyskretnych, np. rozkładu Poissona lub ujemnego dwumianowego. To wiąże się nie tylko z zamianą rozkładu w obliczeniach, ale także ze zmianą sposobu, w jaki podchodzimy do problemu, np. przy rozkładach dyskretnych nie możemy oczekiwać, że istnieje moment, w którym ilość towaru w magazynie wynosi dokładnie  Najczęstszą konsekwencją takiego założenia jest zbyt późne zamawianie względem modelu i nieosiąganie zadanych poziomów obsługi klienta.
Najczęstszą konsekwencją takiego założenia jest zbyt późne zamawianie względem modelu i nieosiąganie zadanych poziomów obsługi klienta.
W zespole Data Science naszym głównym zadaniem jest modyfikowanie bazowych modeli poprzez ulepszanie i rozwijanie pożądanych funkcjonalności. Dla modelu optymalnego zamawiania są to m.in. uwzględnienie zmienności czasu dostawy, modelowanie opóźnień w centralnych magazynach, rozpatrywanie wielu różnych dostawców, agregacja oraz redystrybucja zamówień i wiele innych. Kluczem jest wymyślenie (lub znalezienie w literaturze) takiego modelu, który balansuje teoretyczne wyrafinowanie z praktycznymi możliwościami implementacyjnymi i dostępnymi danymi. Czasami warto wybrać mniej dokładny model, który pozwala na prostsze i szybsze obliczenia. Warto uświadomić sobie tutaj rozmiar danych, z którymi mamy do czynienia - są to dziesiątki milionów zależnych od siebie części z kilkuletnią historią.