„Co jest grane” w dylematach społecznych
Dylemat społeczny to sytuacja grupy ludzi, w której interes jednostki nie jest zbieżny z interesem grupy - występuje konflikt między interesem prywatnym a zbiorowym. Charakteryzuje się tym, że jeżeli członkowie grupy postąpią zgodnie ze swoimi indywidualnymi interesami, to zyskają mniej, niż gdyby brali przede wszystkim pod uwagę w swoich działaniach interes grupy. Jeżeli jednak wszyscy mieliby postąpić zgodnie z interesem grupy, to osoba, która jako jedyna zmieni decyzję i postąpi zgodnie ze swoim indywidualnym interesem, zyska więcej, niż gdyby działała zgodnie z interesem grupy.
Wiele globalnych problemów ma charakter dylematu społecznego, np. zanieczyszczanie lub niszczenie środowiska naturalnego, konflikty zbrojne, realizacja wspólnych projektów ekonomicznych, socjalnych itp. Dylematy społeczne występują również w małych, np. dwuosobowych grupach. Zaczniemy właśnie od takiego przykładu.
Przykład 1. Każda z dwóch osób (graczy) decyduje, nie wiedząc, jaka jest decyzja drugiej strony, czy chce dostać, np. w złotówkach, 1000 (nazwijmy to akcją D), czy też druga osoba ma dostać 2000 (akcja C). W wyniku tych decyzji następuje przydział pieniędzy. Zakładamy anonimowość graczy: osoby te się nie znają i nigdy się nie poznają, decyzja gracza nie jest i nigdy nie będzie znana przez nikogo innego, włącznie z anonimowym systemem czy instytucją, która przydziela kwoty. Zakładamy też racjonalność graczy: gracza nie interesuje, ile dostanie drugi (przeciwnik), a jedynie, ile dostanie on sam. No i że każdy woli więcej niż mniej...
Wybierzesz C czy D, będąc jednym z graczy? Jeśli obaj wybierzecie (zagracie) C, to dostaniecie po 2000, jeżeli D, to po 1000. Naturalne wydawałoby się, że gracze zagrają C. Jeżeli uważasz, że przeciwnik też myśli w ten sposób, czyli zagra C, to możesz ulec pokusie, by zagrać D. Dlaczego? Bo wtedy dostaniesz 1000 za swoją decyzję oraz 2000 w wyniku decyzji C przeciwnika, czyli razem 3000! Ale przeciwnik też może pomyśleć, że zagrasz C, więc także u niego może pojawić się pokusa, by zagrać D, aby otrzymać łącznie 3000. Jeżeli obaj tak zagracie, to dostaniecie po 1000. Co gorsza, jeżeli zagrasz C, a przeciwnik ulegnie pokusie (czyli zagra D), to nic nie dostaniesz!
Opisana sytuacja to dylemat społeczny. Jako interes grupy dwóch graczy przyjmiemy zagranie C przez obu (dostają wtedy po 2000). Interes indywidualny gracza to ulegnięcie pokusie (z perspektywą otrzymania 3000), czyli zagranie D. Jeżeli jednak obaj gracze postąpią zgodnie ze swoim indywidualnym interesem, to dostaną po 1000. Istnieją różne typy dylematów społecznych. Zajmiemy się modelami matematycznymi dylematów. Opiszemy wpierw najprostsze ciekawe sytuacje.
Niech grupa składa się z dwóch nierozróżnialnych graczy, mających do wyboru, tak jak w omawianym wyżej przykładzie, tylko dwie akcje (strategie): C - współpracować, lub D - zdradzić (od ang. cooperate-defect). Będziemy zakładać, że gracze są racjonalni, a ich decyzje anonimowe. W wyniku podjętych akcji gracze otrzymują wypłaty, określone tzw. macierzą gry:
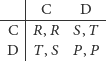 |
(1) |
Pierwsza współrzędna każdej pary wypłat w macierzy oznacza wypłatę gracza wierszowego (inaczej: pierwszego), gdy gra strategię numerującą ten wiersz, druga - gracza kolumnowego (drugiego), gdy gra strategię numerującą kolumnę. Przykładowo: w parze 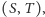 gdy gracz wierszowy gra C, a kolumnowy gra D, wypłatą gracza wierszowego jest
gdy gracz wierszowy gra C, a kolumnowy gra D, wypłatą gracza wierszowego jest 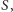 a kolumnowego -
a kolumnowego - 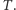 W ten sposób uzyskaliśmy (skończoną) dwuosobową grę strategiczną. Ogólnie:
W ten sposób uzyskaliśmy (skończoną) dwuosobową grę strategiczną. Ogólnie:
Definicja 1. (Skończona) 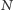 -osobowa gra strategiczna jest to trójka:
-osobowa gra strategiczna jest to trójka:
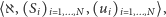 |
(2) |
gdzie 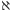 to zbiór
to zbiór 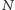 graczy,
graczy, 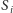 - skończony zbiór strategii gracza
- skończony zbiór strategii gracza 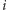 (może być inny dla każdego gracza),
(może być inny dla każdego gracza), 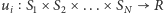 - funkcja wypłaty gracza
- funkcja wypłaty gracza 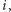 dla
dla 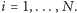
Omówimy trzy sytuacje - gry dwuosobowe opisane powyższą macierzą wypłat - które - na razie intuicyjnie - uznamy za dylematy społeczne. W każdej z nich zbiór strategii każdego gracza to 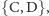 a wypłaty, czyli wartości funkcji wypłat z (2), to odpowiednie wyrazy ogólnej macierzy wypłat (1).
a wypłaty, czyli wartości funkcji wypłat z (2), to odpowiednie wyrazy ogólnej macierzy wypłat (1).
- 1.
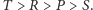 Każdą grę spełniającą te nierówności nazwiemy dylematem więźnia. Przykład 1 jest taką grą, gdyż
Każdą grę spełniającą te nierówności nazwiemy dylematem więźnia. Przykład 1 jest taką grą, gdyż 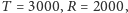
 Nazwa wiąże się z pewną historyjką "śledczo-więzienną". Wybrałem jednak inną (jej autorem jest noblista, Robert Aumann), by pokazać, że dylemat więźnia niekoniecznie musi się rozgrywać w areszcie...
Nazwa wiąże się z pewną historyjką "śledczo-więzienną". Wybrałem jednak inną (jej autorem jest noblista, Robert Aumann), by pokazać, że dylemat więźnia niekoniecznie musi się rozgrywać w areszcie...- 2.
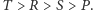 Każdą grę spełniającą te nierówności nazwiemy grą zamieć śnieżna.
Każdą grę spełniającą te nierówności nazwiemy grą zamieć śnieżna.

Przykład 2. Dwóch kierowców (graczy) siedzi w unieruchomionych autach, po przeciwnych stronach zasypanej przez lawinę drogi. Aby drogę odśnieżyć, należy zużyć 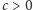 energii. Oznaczmy
energii. Oznaczmy 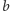 - korzyść każdego gracza z odśnieżenia drogi (a więc np. z dojechania do domu), przy czym
- korzyść każdego gracza z odśnieżenia drogi (a więc np. z dojechania do domu), przy czym 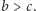 Każdy podejmuje samodzielnie decyzję, czy odśnieżyć drogę (strategia C), czy czekać w aucie (strategia D). Zakładamy że jeśli obaj odśnieżają, to tracą
Każdy podejmuje samodzielnie decyzję, czy odśnieżyć drogę (strategia C), czy czekać w aucie (strategia D). Zakładamy że jeśli obaj odśnieżają, to tracą 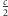 energii każdy. Zakładamy też racjonalność i anonimowość graczy, oraz że decyzje graczy nie wpływają na ich reputację (choć nie wiem, czy nie chciałbym wpłynąć na reputację wygrzewającego się w aucie z drugiej strony lawiny, gdybym sam odśnieżył drogę...
energii każdy. Zakładamy też racjonalność i anonimowość graczy, oraz że decyzje graczy nie wpływają na ich reputację (choć nie wiem, czy nie chciałbym wpłynąć na reputację wygrzewającego się w aucie z drugiej strony lawiny, gdybym sam odśnieżył drogę...
Grę opisuje macierz wypłat

 Jeżeli założyć, że drugi gracz gra C (odśnieża, bo też chce wrócić do domu!), to lepiej jest zostać w aucie
Jeżeli założyć, że drugi gracz gra C (odśnieża, bo też chce wrócić do domu!), to lepiej jest zostać w aucie  No, ale drugi też może tak przebiegle rozumować i wtedy obaj zamarzną (wypłata 0). Mamy w ogólnych oznaczeniach wypłat gry dwuosobowej:
No, ale drugi też może tak przebiegle rozumować i wtedy obaj zamarzną (wypłata 0). Mamy w ogólnych oznaczeniach wypłat gry dwuosobowej:  a więc Przykład 2 opisuje grę zamieć śnieżna.
a więc Przykład 2 opisuje grę zamieć śnieżna.
- 3.
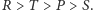 Każdą grę spełniającą te nierówności nazwiemy grą polowanie na jelenia.
Każdą grę spełniającą te nierówności nazwiemy grą polowanie na jelenia.
Przykład 3. Dwóch myśliwych może zapolować na jelenia (strategia C) lub na zające (strategia D). Ich decyzje zapadają jednocześnie i niezależnie, anonimowo, bez straty reputacji. Jeleń ma wartość 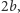 zające po
zające po 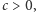 przy czym
przy czym 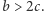 Jeśli obaj zapolują na jelenia, to upolują go, dzieląc zysk po równo, czyli otrzymując po
Jeśli obaj zapolują na jelenia, to upolują go, dzieląc zysk po równo, czyli otrzymując po 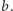 Jeśli pierwszy zagra C, drugi D, to pierwszy nic nie upoluje, czyli otrzymuje 0, drugi upoluje dwa zające i otrzymuje
Jeśli pierwszy zagra C, drugi D, to pierwszy nic nie upoluje, czyli otrzymuje 0, drugi upoluje dwa zające i otrzymuje 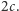 Jeśli obaj zagrają D, to upolują po jednym zającu (wypłata
Jeśli obaj zagrają D, to upolują po jednym zającu (wypłata  dla każdego).
dla każdego).
Macierz wypłat graczy ma postać

 a więc rzeczywiście odpowiada ona grze polowanie na jelenia (często przyjmuje się że wypłata ze strategii D jest równa
a więc rzeczywiście odpowiada ona grze polowanie na jelenia (często przyjmuje się że wypłata ze strategii D jest równa  niezależnie od tego, co gra partner; nie zmienia to podstawowych własności matematycznych tej gry).
niezależnie od tego, co gra partner; nie zmienia to podstawowych własności matematycznych tej gry).
Jakie strategie wybiorą myśliwi? Gdyby byli pewni, że partner (tu raczej partner, a nie przeciwnik) ma pewną rękę i jak wyceluje, to na pewno trafi, to chyba nie ma wątpliwości, że należy grać C 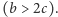 Ale co zagramy, gdy partner miał np. nieprzespaną noc lub podejrzewamy, że ulegnie pokusie strzelenia do tego, co się nawinie, a my nie możemy wrócić z pustymi rękami? Albo że partner nie ma do nas pełnego zaufania, że trafimy, a także nie może do domu wrócić z pustymi rękami i dlatego wymierzy raczej w zająca (założyliśmy, że trafienie zająca jest pewne)? Wtedy decyzja o wyborze strategii nie jest już tak oczywista.
Ale co zagramy, gdy partner miał np. nieprzespaną noc lub podejrzewamy, że ulegnie pokusie strzelenia do tego, co się nawinie, a my nie możemy wrócić z pustymi rękami? Albo że partner nie ma do nas pełnego zaufania, że trafimy, a także nie może do domu wrócić z pustymi rękami i dlatego wymierzy raczej w zająca (założyliśmy, że trafienie zająca jest pewne)? Wtedy decyzja o wyborze strategii nie jest już tak oczywista.
Podaliśmy trzy przykłady gier dwuosobowych, każda z innym układem nierówności na parametry  i z (intuicyjnie) innego typu "dylematem". No dobrze, ale przecież istnieje jeszcze 21 innych układów ostrych nierówności spełnianych przez te parametry.
i z (intuicyjnie) innego typu "dylematem". No dobrze, ale przecież istnieje jeszcze 21 innych układów ostrych nierówności spełnianych przez te parametry.
Sformułujemy definicję dylematu społecznego dla ogólnej klasy gier. Okaże się że obejmuje ona ważne i interesujące w zastosowaniach gry wieloosobowe, a dla gier dwuosobowych "zostawia" jedynie gry opisane w Przykładach 1, 2, 3!
Rozważamy zbiór  złożony z
złożony z 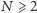 racjonalnych graczy, mających do wyboru strategię C lub D. Niech
racjonalnych graczy, mających do wyboru strategię C lub D. Niech 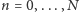 oznacza liczbę osób grających C. Zakładamy, że gracze są nierozróżnialni, a więc wystarczy określić wypłatę osoby grającej C i osoby grającej D dla wszystkich argumentów
oznacza liczbę osób grających C. Zakładamy, że gracze są nierozróżnialni, a więc wystarczy określić wypłatę osoby grającej C i osoby grającej D dla wszystkich argumentów 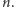 Zakładamy pełną anonimowość i racjonalność graczy. Niech
Zakładamy pełną anonimowość i racjonalność graczy. Niech 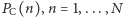 oznacza wypłatę gracza grającego C (C-gracza), a
oznacza wypłatę gracza grającego C (C-gracza), a 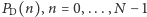 - wypłatę D-gracza, zwrot "mieć lepiej" (gorzej) oznacza mieć wyższą (niższą) wypłatę. Zakładamy dla uproszczenia, że wszystkie wypłaty są różne.
- wypłatę D-gracza, zwrot "mieć lepiej" (gorzej) oznacza mieć wyższą (niższą) wypłatę. Zakładamy dla uproszczenia, że wszystkie wypłaty są różne.
- Cały artykuł dostępny jest w wersji do druku [application/pdf]: (320 KB)