Artykuł ten poświęcony jest przykładowi, który ilustruje uniwersalność zastosowań matematyki: modelowaniu tzw. inwazji zombie - będącej popularnym tematem horrorów. Z praktycznego punktu widzenia zombie (często w przeciwieństwie do ludzi) są idealni do matematycznego modelowania, gdyż występują w dużych, podobnie zachowujących się grupach, działają praktycznie bez udziału świadomości i przemieszczają się bez widocznego celu, więc można zakładać, że czynią to w sposób losowy.

Model inwazji zombie zaczerpnięto z epidemiologii - "zombizm" został potraktowany jako choroba zakaźna. Opisuje on dynamikę zmian przynależności członków pewnej populacji do grup: zdrowych (lecz podatnych na infekcję), zarażonych chorobą zakaźną (zazombionych) i martwych. Same równania tworzone są na podstawie szacowanego prawdopodobieństwa kontaktu osoby zdrowej i zarażonej oraz prawdopodobieństwa zarażenia w przypadku takiego kontaktu. W modelach związanych z inwazją zombie pojawia się nowy element: osoby zaklasyfikowane jako zmarłe mogą powracać do modelu jako zarażone "zombizmem". Pierwsze matematyczne modele inwazji zombie przedstawiła grupa studentów pod kierownictwem profesora Roberta J. Smith?'a (to nie jest literówka, autor artykułu faktycznie nazywa się Smith? ze znakiem zapytania na końcu) z uniwersytetu w Ottawie w pracy When zombies attack!: Mathematical modelling of an outbreak of zombie infection w 2009 roku. Niniejszy artykuł jest prezentacją wyników ich "badań".

1. Model podstawowy

Przez 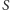oznaczamy liczbę ludzi niezarażonych, ale podatnych na "zombizm" (zakładamy, że nie ma ludzi, którzy są odporni na zarazę). Przez 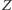oznaczamy liczbę aktywnych, zarażających zombie, zaś przez 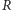- liczbę zmarłych. Prawdopodobieństwo spotkania zombie i "zdrowego" człowieka jest proporcjonalne do iloczynu 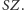Współczynnik 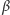odpowiada za prawdopodobieństwo tego, że w wyniku takiego spotkania człowiek zostanie zarażony, a 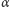za prawdopodobieństwo tego, że zombie zginie (oczywiście, zgodnie z wiedzą, jaką wynosimy z horrorów, 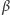jest znacząco większe niż 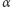). Dodatkowo zakładamy, że ludzie mogą umierać z powodów niezwiązanych z inwazją (o umieralności decyduje parametr 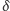), a zmarli mogą przemieniać się w zombie (o czym decyduje parametr 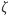). Wpływ przyrostu naturalnego ludzi został pominięty ze względu na założenie (pochodzące z "obserwacji") o krótkim czasie trwania inwazji zombie.

Wnioski płynące z rozwiązania modelu nie są zbyt optymistyczne. Powstają dwa punkty równowagi odpowiadające sytuacji braku zombie oraz całkowitej zagłady ludzkości. Niestety, tylko ten drugi okazuje się być stabilny (prawie) niezależnie od wartości parametrów. Nawet jeżeli na świecie nie ma ani jednego zombie, w każdej chwili jakaś jednostka może powstać z grobu, rozpoczynając kolejną inwazję. Jeżeli ta się nie powiedzie i na świecie ponownie nie będzie ani jednego zombie, kolejna inwazja to tylko kwestia czasu. Któraś inwazja w końcu będzie skuteczna... Zatem zombie i ludzie w tym scenariuszu nie mogą współistnieć. Praktycznie pewne jest, że w końcu zombie zainfekują wszystkich ludzi.

Jednakże utwory na temat zombie dostarczają szerokiej palety rozwiązań problemu: od kwarantanny, przez znalezienie lekarstwa, po bezpośrednią walkę zbrojną z potworami. Warto też uwzględnić, że ludzie nie muszą stawać się zombie natychmiast. Może któreś z tych założeń pozwoli ludzkości przetrwać apokalipsę?

2. Modele rozbudowane

Pierwszą poprawką do modelu podstawowego jest wprowadzenie nowej kategorii: 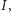czyli zainfekowanych. Zgodnie z zasadami większości filmów ludzie zaatakowani przez zombie przez pewien okres podlegają stopniowej przemianie, w trakcie której nie są jeszcze zagrożeniem dla innych. Zainfekowani nadal mogą umrzeć, zanim zmienią się w zombie (z tym samym prawdopodobieństwem 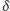). W innym przypadku przechodzą do grupy 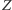(z parametrem 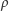) odpowiadającym za prędkość przemiany.

Analizując dynamikę układu, znów otrzymujemy dwa punkty równowagi: odpowiadający za zupełny brak zombie i za kompletną zagładę ludzkości. Niestety, znów tylko ten drugi okazuje się być stabilny, czyli i w tym przypadku zombie w końcu zainfekują wszystkich. Dzieje się to jednak wolniej niż w modelu podstawowym, co można zaobserwować na wykresach (użyto parametrów: ).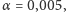

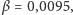
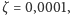
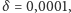
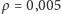W każdym z przykładów w chwili 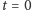populacja ludzi liczy 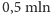, natomiast zombie nie występują. W modelu podstawowym po czasie 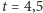nie ma już żywego człowieka. Natomiast w modelu opóźnionym ludzki gatunek wymarł po czasie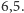

Dodajmy do modelu kolejny element - kwarantannę - być może to pomoże w ocaleniu ludzkości. Ludzie zainfekowani lub zmienieni w zombie mogą być poddani kwarantannie, czyli usunięci z populacji i niezdolni zarażać. Tę grupę oznaczamy przez 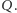Za możliwość schwytania i umieszczenia pod kwarantanną osób niebezpiecznych odpowiadają parametry 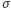i 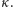Z kolei parametr 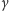oznacza prawdopodobieństwo podjęcia próby ucieczki spod kwarantanny. By spojrzeć na sprawę optymistyczniej, zakłada się, że teren kwarantanny jest chroniony idealnie, więc wszystkie próby ucieczki kończą się śmiercią (przy czym zabici w ten sposób też mogą powrócić jako zombie).

Punkty równowagi modelu z kwarantanną nie różnią się od poprzednich. Są nimi: kompletny brak zombie oraz zupełny brak zdrowych ludzi. Ale tym razem stabilność jest bardziej delikatną kwestią.

Okazuje się, że brak zombie jest stabilnym punktem równowagi wtedy i tylko wtedy, gdy tzw. współczynnik reprodukcji 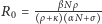jest mniejszy od 1 (dla dużych 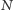- liczby niezainfekowanych - można użyć przybliżenia 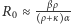). W innym przypadku stabilnym punktem stałym jest punkt zagłady.

Teoretycznie sytuacja jest lepsza niż w pierwszych dwóch modelach. Jeśli zakładamy (zombie są większym zagrożeniem dla ludzi niż ludzie dla zombie), to decydującym czynnikiem staje się szybkie wykrycie i izolowanie zainfekowanych (współczynnik 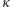). Jednakże ze względu na problemy techniczne (trudność wykrywania zainfekowanych oraz stworzenia i utrzymania terenu kwarantanny) mało prawdopodobne są duże współczynniki i 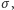więc można spodziewać się 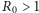i scenariusza zagłady ludzi (wolniejszej niż w poprzednich modelach). Zatem zorganizowanie systemu kwarantanny nie daje ludzkości wielkiej nadziei na przetrwanie.

W kolejnym modelu zapominamy o kwarantannie. Zresztą nie jest już potrzebna, gdyż tym razem naukowcy wynaleźli możliwe do natychmiastowego wyprodukowania lekarstwo na "zombizm". Skoro dysponujemy lekarstwem, nie potrzebujemy kwarantanny, ponieważ leczymy wszystkich, których moglibyśmy odosobnić. Wyleczone zombie stają się na powrót ludźmi (szansę na to oznaczamy przez ), lecz wciąż są podatne na ponowne zarażenie. Nieco optymistyczne jest założenie, że wyleczyć można każdego, niezależnie od tego, w jaki sposób został zombie i w jakim jest stanie.

Jest to pierwszy model, w którym ludzie i zombie mogą współistnieć. Dzięki składnikowi 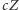stabilnym punktem równowagi tego układu jest:

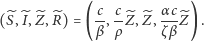
Jak widać liczba ludzi, którzy będą koegzystować z zombie, zależy głównie od efektywności leczenia: 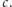Według przewidywań liczba ta byłaby niewielka (patrz wykres).

Ponieważ wszystkie "pokojowe" metody pozostawiają ludzkość w sytuacji nie do pozazdroszczenia (albo ludzie wymrą doszczętnie, albo zostanie garstka koegzystująca z zombie), zdecydowanie zalecane są metody "niepokojowe". Załóżmy, że po zgromadzeniu odpowiedniej ilości zasobów (np. broni, amunicji, przeszkoleniu żołnierzy) ludzkość może wykonać strategiczny kontratak, niszcząc część populacji zombie. Pomiędzy atakami musi upłynąć trochę czasu, by uzupełnić zasoby i skoordynować działania. W każdym ataku ludzkość musi zniszczyć (procentowo) coraz więcej zombich. Analiza wszystkich scenariuszy doprowadziła autorów do wniosku, że w przypadku ataku zombie trzeba działać szybko i agresywnie, jeśli ludzkość ma przetrwać.

Warto zwrócić uwagę również na inne naukowe podejścia do tematyki zombie. Np. w Is It Safe To Go Out Yet? Statistical Inference in a Zombie Outbreak Model, na podstawie modeli z przytoczonej pracy autorzy B. Calderhead, M. Girolami, D.J. Higham, próbują z wykorzystaniem metod statystycznych obliczyć optymalny moment opuszczenia kryjówki w zależności od obserwacji liczby zombie w okolicy. Z kolei A. Chodorow w pracy Death and Taxes and Zombies bada prawno-podatkowe konsekwencje pojawienia się nieumarłych (przede wszystkim zombie, ale też wampirów), dochodząc do miłego politykom wniosku, że śmierć nie powinna być podstawą do uniknięcia opodatkowania i zombie również powinny się dołożyć do "umowy społecznej".

Czy wszystko to, co opisałem, jest tylko matematyczną zabawką, bez żadnych zastosowań (oczywiście, jeżeli nie wierzymy w ewentualność takiej inwazji)? Okazuje się, że nie do końca. Podobnymi modelami, w których "usunięci z zakresu zainteresowań" mogą do modelu powracać, można opisać choroby przechodzące w postać uśpioną, takie jak wirusowe zapalenia wątroby i niektóre grzybice. Takie sytuacje mogą też zachodzić w modelach niezwiązanych z medycyną, takich jak dynamika organizacji społecznych (np. partii politycznych). Jednakże sam Robert J. Smith? zwrócił uwagę na najbardziej spektakularne znaczenie swojego artykułu: pobudzanie zainteresowania matematyką i matematycznym modelowaniem wśród szerokiej publiczności. Informacje o matematykach badających inwazję zombie pojawiły się we wszystkich najbardziej znanych amerykańskich i kanadyjskich gazetach. Smith? twierdzi, że otrzymał tysiące wiadomości tylko o szkolnych projektach matematycznych zainspirowanych tą pracą, nie mówiąc już o pojedynczych osobach zachęconych do tak niebanalnej nauki. Powinno to stawiać twórców programu szkolnej matematyki i nauczycieli przed niepokojącym pytaniem: jak bardzo przerażająca musi być dla uczniów matematyka, skoro dopiero towarzystwo zombie czyni ją bardziej przyjazną i interesującą?