Podobno Bóg nie gra z wszechświatem w kości, na potrzeby naszych rozważań wyobraźmy sobie jednak, że codziennie o świcie bierze On do Ręki symetryczną kość do gry o przystających, foremnych ścianach. Ze względu na swoją Wszechmocność Bóg nie jest ograniczony wynikami Platona dotyczącymi liczby takich wielościanów, nie czynimy więc w tym momencie żadnych założeń dotyczących 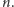Następnie kość jest rzucana i jeśli liczba wyrzuconych oczek przekroczy 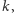to 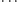cóż, jako ludzkość kibicujemy wartościom nie większym od 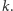Postaramy się teraz zaproponować rozsądną wartość parametru 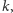posługując się wiedzą, że przy dotychczasowej liczbie 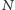rzutów (którą możemy przybliżyć przez 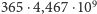) nie zaobserwowaliśmy jeszcze żadnej Apokalipsy.

Zauważmy, że w zależności od 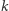prawdopodobieństwo sukcesu (traktowanego jako kolejny dzień w historii ludzkości) wynosi

Dość przekonująco wygląda teraz pomysł wyboru takiego 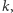które będzie maksymalizowało powyższą funkcję 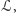zwaną w statystycznym żargonie funkcją wiarogodności. W pewnym sensie ustanowilibyśmy w ten sposób obserwowaną sytuację "najbardziej prawdopodobną", co wydaje się rozsądnym podejściem. Tak otrzymany estymator wartości 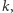zwany estymatorem największej wiarogodności, wynosi

gdzie 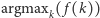oznacza taką wartość 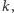dla której 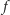przyjmuje największą wartość. Jest to jednak mało emocjonujący wynik - oznaczałby przecież, że szansa na kolejny świt bez globalnej katastrofy wynosi 1, co stawiałoby pod znakiem zapytania przyszłość szeregu hollywoodzkich superprodukcji. Przeprowadźmy więc inną analizę - rozpocznijmy od założenia, że gdybyśmy nie byli świadkami 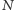dni bez Apokalipsy, traktowalibyśmy każdą z wartości 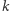jako równie prawdopodobną. Jest to nasze założenie a priori odnośnie prawdopodobieństwa poszczególnych wartości 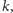ilustrujące stan naszej wiedzy (tudzież niewiedzy) dotyczącej tego parametru. Zobaczmy teraz, w jaki sposób wiedza o naszym istnieniu rzutuje na wspomniane założenie - w tym celu posłużymy się wzorem Bayesa, pozwalającym na "odwracanie warunkowania" przy obliczaniu prawdopodobieństw warunkowych

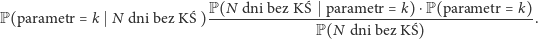(1)

Z założenia o jednostajności rozkładu parametru bez uwzględniania obserwacji stwierdzamy, że 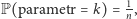ponadto oczywiście

Moglibyśmy teraz, korzystając ze wzoru na prawdopodobieństwo całkowite, pracowicie obliczyć mianownik prawej strony równości (1), zamiast tego posłużymy się jednak popularnym w podobnych wnioskowaniach fortelem. Zauważmy bowiem, że lewa strona równości (1) jest funkcją 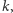której wartości na argumentach ze zbioru 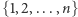sumują się do 1 (gdyż stanowi ona rozkład prawdopodobieństwa na tym zbiorze). Z wcześniejszych obliczeń wynika, że z dokładnością do proporcjonalności ta funkcja wynosi 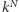(wartość 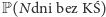nie zależy od 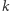), w związku z czym, aby spełniony był warunek sumowania się do 1 na zbiorze 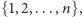musi być

Otrzymaliśmy w ten sposób rozkład a posteriori badanego parametru, czyli "zweryfikowany" przez nasze obserwacje rozkład a priori.

Wszystko pięknie - zwróci uwagę Czytelnik Niecierpliwy - ale ja ciągle nie wiem, jaka jest szansa na jutrzejszy koniec świata. Istotnie, żadna propozycja estymatora wartości parametru nie została jeszcze przedstawiona. Dysponujemy jednak odpowiednim rozkładem prawdopodobieństwa, co wydaje się nieść więcej informacji niż przedstawienie jednej liczby. Jeśli jednak komuś zależy na konkretnym wyniku, może posłużyć się wartością oczekiwaną otrzymanego rozkładu, która wynosi

Wobec tego za prawdopodobieństwo uniknięcia Apokalipsy możemy przyjąć

gdzie przez 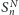oznaczyliśmy sumę 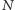-tych potęg kolejnych liczb naturalnych. W tym momencie przypominamy sobie pewien kłopotliwy szkopuł - nie znamy wartości 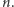Możemy jednak przypuszczać, że Bóg nie zadowoliłby się ordynarną kostką sześcienną; intuicja podpowiada, że w grę wchodzą kości o liczbie ścian przekraczającej liczbę ziaren piasku na Ziemi lub gwiazd na niebie. W tej sytuacji rozsądne wydaje się zbadanie, w jaki sposób powyższe wyrażenie zachowuje się przy zbiegającym do nieskończoności. W tym celu zauważmy, że

co po odjęciu obustronnie 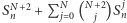i podzieleniu przez 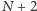prowadzi do rekurencyjnego wzoru

Możemy stąd za pomocą prostej indukcji wywnioskować, że 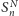jest wielomianem od 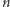stopnia 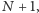o współczynniku przy najwyższej potędze równym 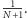W tej sytuacji 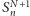oraz 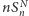są wielomianami od 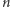o równym stopniu, zatem granica ich ilorazu, przy zbiegającym do nieskończoności, jest ilorazem ich współczynników przy najwyższej potędze, czyli 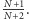Jeśli zaś estymujemy prawdopodobieństwo Zniszczenia Świata przez 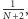to wartość oczekiwana liczby dni, jaka nam została do tego zdarzenia, wynosi 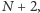czyli drugie tyle, co już było i jeszcze dwa dni (trzeciego skończy grać Wielka Orkiestra Świątecznej Pomocy).

Oczywiście, powyższe rozważania nie mogą być traktowane poważnie, ilustrują jednak dwie poważne koncepcje wnioskowania statystycznego - klasyczną oraz bayesowską. Fundamentalną różnicą między nimi jest dopuszczenie przez podejście bayesowskie rozkładu prawdopodobieństwa na zbiorze możliwych parametrów. Zasadność takiej operacji może budzić wątpliwości - tworzymy wówczas w naszym wnioskowaniu kolejne (po wyborze rodziny rozkładów rządzących doświadczeniem) czysto uznaniowe ogniwo, jakim jest wybór rozkładu a priori na zbiorze parametrów. Z drugiej strony jednak ta uznaniowość zwiększa elastyczność naszego modelu, gdyż pozwala uwzględnić eksperckie "widzimisię" dotyczące parametrów; ponadto, kiedy już ów rozkład zostanie przyjęty, cała reszta naszej dedukcji to czysto probabilistyczne obliczenia, co niekoniecznie jest prawdą w przypadku podejścia klasycznego. Spór między zwolennikami tych metodologii trwa, a na jego rozwiązanie nie pozostało wiele czasu - zgodnie z informacjami zamieszczonymi w angielskiej Wikipedii najbliższy Koniec Świata już w marcu.