Równanie Naviera–Stokesa

Rozważmy przepływ nieściśliwego płynu w pewnym obszarze  Załóżmy, że wiemy, jaka jest prędkość płynu w każdym punkcie obszaru, to znaczy że znamy pole prędkości, oznaczone
Załóżmy, że wiemy, jaka jest prędkość płynu w każdym punkcie obszaru, to znaczy że znamy pole prędkości, oznaczone  w chwili początkowej
w chwili początkowej 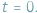 Jak będzie wyglądało pole prędkości płynu
Jak będzie wyglądało pole prędkości płynu 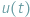 w dowolnym momencie
w dowolnym momencie 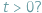
Odpowiedzi na to pytanie szuka się w oparciu o równanie Naviera-Stokesa. Jest ono zapisaną formalnie regułą, która mówi, jak zmienia się w czasie prędkość płynu. Oczywiście, wektor prędkości  zależy od zmiennej przestrzennej
zależy od zmiennej przestrzennej  oraz od czasu
oraz od czasu 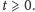 Rozwiązanie równania Naviera-Stokesa z warunkiem początkowym
Rozwiązanie równania Naviera-Stokesa z warunkiem początkowym 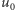 to funkcja
to funkcja 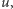 która spełnia to równanie dla czasów dodatnich i w sposób ciągły osiąga warunek początkowy dla
która spełnia to równanie dla czasów dodatnich i w sposób ciągły osiąga warunek początkowy dla 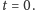
Kłopot w tym, że do dziś nie wiemy, czy równanie Naviera-Stokesa można jednoznacznie rozwiązać dla każdego sensownego (to znaczy takiego, który ma skończoną energię) warunku początkowego 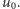 Pomimo niemal stu lat intensywnych badań tego zagadnienia nadal nie wiemy, czy rzeczywiście potrafimy przewidywać przepływ cieczy. Nie wiemy bowiem, czy początkowo ograniczone i gładkie pole prędkości może w pewnej chwili wybuchnąć, czyli osiągnąć w pewnym punkcie
Pomimo niemal stu lat intensywnych badań tego zagadnienia nadal nie wiemy, czy rzeczywiście potrafimy przewidywać przepływ cieczy. Nie wiemy bowiem, czy początkowo ograniczone i gładkie pole prędkości może w pewnej chwili wybuchnąć, czyli osiągnąć w pewnym punkcie 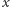 obszaru
obszaru 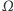 nieskończoną wartość, jednocześnie cały czas ewoluując do tego momentu zgodnie z równaniem Naviera-Stokesa. Jest to sytuacja krępująca: ciężko bowiem się przyznać, że nie potrafimy rozstrzygnąć, czy podstawowy model w hydrodynamice ma sens
nieskończoną wartość, jednocześnie cały czas ewoluując do tego momentu zgodnie z równaniem Naviera-Stokesa. Jest to sytuacja krępująca: ciężko bowiem się przyznać, że nie potrafimy rozstrzygnąć, czy podstawowy model w hydrodynamice ma sens 
Składniki równania
Równanie Naviera-Stokesa to w zasadzie II zasada dynamiki Newtona 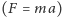 zastosowana do płynu. Mówi ono, że wpływ na tempo
zastosowana do płynu. Mówi ono, że wpływ na tempo 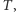 w jakim w danym punkcie zmienia się prędkość płynu, mają cztery składniki:
w jakim w danym punkcie zmienia się prędkość płynu, mają cztery składniki:
- A
- "dyfuzja" prędkości, czyli swego rodzaju uśrednianie prędkości (proces podobny do tego, gdy barwnik dyfunduje w wodzie i ostatecznie jednorodnie zabarwia szklankę);
- B
- "unoszenie" prędkości płynu, czyli konwekcja (tzw. składnik nieliniowy);
- C
- siły związane z ciśnieniem (tzw. gradient ciśnienia);
- D
- siły zewnętrzne (np. grawitacja).
W dalszym ciągu pominiemy siły zewnętrzne, przyjmując  Równanie Naviera-Stokesa można więc wtedy zapisać w nieco naiwny sposób jako
Równanie Naviera-Stokesa można więc wtedy zapisać w nieco naiwny sposób jako

lub bardziej konkretnie, z użyciem odpowiednich symboli:
 |
(1) |
W powyższym wzorze liczba  mierzy lepkość płynu (tzn. to, czy jest on bardziej podobny do miodu czy do wody), a pozostałe symbole związane są z różniczkowaniem. W związku z tym konieczna jest pewna uwaga. Do zrozumienia tego tekstu nie jest konieczne rozumienie powyższych symboli. Czytelnicy, którzy z pochodnymi cząstkowymi nie mieli dotąd do czynienia, mogą spokojnie ignorować zapis formalny i czytać sam tekst, spoglądając na symbole jak na graficzne identyfikatory pojęć, których sens zostanie wyjaśniony poniżej bez technicznych zawiłości.
mierzy lepkość płynu (tzn. to, czy jest on bardziej podobny do miodu czy do wody), a pozostałe symbole związane są z różniczkowaniem. W związku z tym konieczna jest pewna uwaga. Do zrozumienia tego tekstu nie jest konieczne rozumienie powyższych symboli. Czytelnicy, którzy z pochodnymi cząstkowymi nie mieli dotąd do czynienia, mogą spokojnie ignorować zapis formalny i czytać sam tekst, spoglądając na symbole jak na graficzne identyfikatory pojęć, których sens zostanie wyjaśniony poniżej bez technicznych zawiłości.
Równanie (1) uzupełniane jest pewnymi dodatkowymi założeniami:
- w chwili
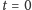 pole prędkości jest równe
pole prędkości jest równe 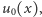
- prędkość
 jest równa zeru na brzegu obszaru
jest równa zeru na brzegu obszaru 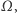
- płyn jest nieściśliwy; oznacza to, że do dowolnej kulki w
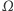 tyle samo płynu wpływa, co wypływa. Pole prędkości zwane jest wtedy bezźródłowym (bezdywergentnym).
tyle samo płynu wpływa, co wypływa. Pole prędkości zwane jest wtedy bezźródłowym (bezdywergentnym).

Rys. 1 Schematyczny obraz działania laplasjanu: wygładzanie rozwiązań z upływem czasu.
Trzech bohaterów
Na równanie Naviera-Stokesa można patrzeć jak na bitwę, w której chodzi o to, czy pierwszy składnik równania (pochodna czasowa  ), a wraz z nią sama prędkość
), a wraz z nią sama prędkość 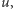 ucieknie czy też nie ucieknie do nieskończoności. Walka ta rozgrywa się między trzema pozostałymi "osobami":
ucieknie czy też nie ucieknie do nieskończoności. Walka ta rozgrywa się między trzema pozostałymi "osobami":
- bohaterem pozytywnym (czyli laplasjanem:
 ),
), - nieliniowym złoczyńcą:
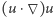 oraz
oraz - "niewidzialnym rozgrywającym" (gradientem ciśnienia:
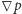 ).
).
Żeby zatem głębiej zrozumieć, co się dzieje w tym równaniu, dlaczego jest ono tak kłopotliwe i dlaczego kolejne składniki zostały tak a nie inaczej nazwane, spróbujmy lepiej zrozumieć charaktery głównych postaci.
Bohater pozytywny
Aby wyjaśnić, dlaczego większość matematyków sądzi, że laplasjan poprawia regularność rozwiązań równania Naviera-Stokesa, przyjrzyjmy się równaniu, w którym występuje tylko pochodna względem czasu i sam laplasjan (przyjmujemy 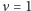 ):
):

z warunkiem początkowym 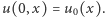 Jest to tzw. równanie przepływu ciepła (tym razem
Jest to tzw. równanie przepływu ciepła (tym razem  oznacza zwykłą funkcję o wartościach rzeczywistych, a nie pole wektorowe), które opisuje, jak zmienia się w czasie temperatura w obszarze, w którym początkowy rozkład temperatury jest dany przez funkcję
oznacza zwykłą funkcję o wartościach rzeczywistych, a nie pole wektorowe), które opisuje, jak zmienia się w czasie temperatura w obszarze, w którym początkowy rozkład temperatury jest dany przez funkcję  Okazuje się, że nawet gdy funkcja
Okazuje się, że nawet gdy funkcja  nie jest zbyt gładka, to funkcje
nie jest zbyt gładka, to funkcje 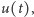 opisujące rozkład temperatury w czasie
opisujące rozkład temperatury w czasie 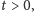 natychmiast stają się niezwykle regularne i gładkie. Ma to związek z efektem uśredniania (charakterystycznym dla dyfuzji), który ostatecznie prowadzi do tego, że rozwiązania
natychmiast stają się niezwykle regularne i gładkie. Ma to związek z efektem uśredniania (charakterystycznym dla dyfuzji), który ostatecznie prowadzi do tego, że rozwiązania 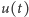 z upływem czasu coraz bardziej upodobniają się do funkcji harmonicznej, to znaczy takiej, która jest ciągła (tak naprawdę gładka) i ma własność wartości średniej: jej średnia wartość w dowolnej kulce jest równa jej wartości w środku kulki. Bliższa analiza pokazuje też, że laplasjan wypompowuje energię z układu tym szybciej, im większe są różnice temperatury (w przypadku równania Naviera-Stokesa: różnice prędkości) i co więcej, dużo szybciej pozbywa się energii ze skal mikroskopijnych niż z tych dużo większych. To przeciwdziała dzikim oscylacjom w małych skalach i wygładza rozwiązanie.
z upływem czasu coraz bardziej upodobniają się do funkcji harmonicznej, to znaczy takiej, która jest ciągła (tak naprawdę gładka) i ma własność wartości średniej: jej średnia wartość w dowolnej kulce jest równa jej wartości w środku kulki. Bliższa analiza pokazuje też, że laplasjan wypompowuje energię z układu tym szybciej, im większe są różnice temperatury (w przypadku równania Naviera-Stokesa: różnice prędkości) i co więcej, dużo szybciej pozbywa się energii ze skal mikroskopijnych niż z tych dużo większych. To przeciwdziała dzikim oscylacjom w małych skalach i wygładza rozwiązanie.

Rys. 2 Rozwiązujemy równanie Burgersa.
- Startujemy z punktu
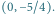 Mamy
Mamy 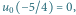 więc rysujemy z punktu
więc rysujemy z punktu 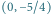 prostą o współczynniku kierunkowym zero. Na tej prostej wartość
prostą o współczynniku kierunkowym zero. Na tej prostej wartość  jest równa zeru.
jest równa zeru. - Startujemy z punktu
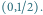 Mamy
Mamy 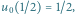 więc rysujemy z punktu
więc rysujemy z punktu 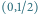 prostą o współczynniku kierunkowym
prostą o współczynniku kierunkowym 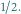 Na tej prostej wartość
Na tej prostej wartość  jest równa
jest równa 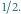
- Startujemy z punktu
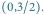 Mamy
Mamy 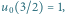 więc rysujemy prostą z punktu
więc rysujemy prostą z punktu 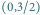 o współczynniku kierunkowym równym 1. Na tej prostej wartość
o współczynniku kierunkowym równym 1. Na tej prostej wartość  jest równa 1.
jest równa 1.
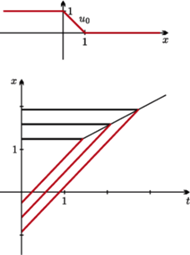
Rys. 3 Dla innego warunku początkowego dochodzimy do sprzeczności: na liniach ukośnych wartość funkcji musi być równa 1, a na poziomych - zero. Niestety, linie się zderzają i nawet wygładzenie warunku początkowego nic na to pomóc nie może  Jak zatem określać rozwiązanie w spornych punktach? Gdzie ma przebiegać linia skoku (fala uderzeniowa)? I czy takie nieciągłe rozwiązania mają w ogóle sens?
Jak zatem określać rozwiązanie w spornych punktach? Gdzie ma przebiegać linia skoku (fala uderzeniowa)? I czy takie nieciągłe rozwiązania mają w ogóle sens?
Nieliniowy złoczyńca
W przeciwieństwie do laplasjanu składnik nieliniowy 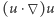 podejrzewany jest przynajmniej o próby (być może nieskuteczne) doprowadzenia prędkości do wartości nieskończonej. Jak się to dzieje? Spójrzmy na równanie, jakie otrzymujemy z równania Naviera-Stokesa po wyrzuceniu laplasjanu
podejrzewany jest przynajmniej o próby (być może nieskuteczne) doprowadzenia prędkości do wartości nieskończonej. Jak się to dzieje? Spójrzmy na równanie, jakie otrzymujemy z równania Naviera-Stokesa po wyrzuceniu laplasjanu

przyjmując warunek początkowy  Ponieważ nadal wymagamy, by
Ponieważ nadal wymagamy, by 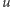 opisywało przepływ nieściśliwy
opisywało przepływ nieściśliwy  to powyższe równanie (zwane równaniem Eulera) jest, z grubsza biorąc, tak samo słabo poznane jak równanie Naviera-Stokesa. Dokonajmy jednak kolejnego uproszczenia: zapomnijmy o warunku przepływu bezźródłowego, a ponadto dla pełnego uproszczenia rozpatrzmy przypadek jednowymiarowy (dla zmiennej przestrzennej). Wówczas
to powyższe równanie (zwane równaniem Eulera) jest, z grubsza biorąc, tak samo słabo poznane jak równanie Naviera-Stokesa. Dokonajmy jednak kolejnego uproszczenia: zapomnijmy o warunku przepływu bezźródłowego, a ponadto dla pełnego uproszczenia rozpatrzmy przypadek jednowymiarowy (dla zmiennej przestrzennej). Wówczas 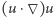 to po prostu
to po prostu 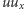 i dostajemy:
i dostajemy:

Takie równanie (zwane równaniem Burgersa) ma dość niepokojące własności. Jakiego rodzaju są to kłopoty, można zrozumieć nawet bez znajomości pochodnych cząstkowych. Istnieje bowiem prosty algorytm rozwiązywania równania Burgersa, gdy tylko ma ono gładkie, regularne rozwiązanie. Robi się to tak. Bierzemy jakikolwiek punkt 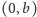 na osi
na osi 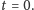 Patrzymy teraz, jaka jest wartość funkcji
Patrzymy teraz, jaka jest wartość funkcji 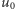 dla
dla  Jeśli jest ona równa
Jeśli jest ona równa 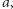 to kreślimy prostą wychodzącą z punktu
to kreślimy prostą wychodzącą z punktu 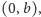 która ma współczynnik kierunkowy
która ma współczynnik kierunkowy 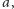 czyli równanie
czyli równanie 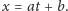 Na wykreślonej prostej definiujemy wartość funkcji
Na wykreślonej prostej definiujemy wartość funkcji  jako liczbę
jako liczbę 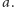 Jeśli teraz pokryjemy takimi prostymi całą półpłaszczyznę
Jeśli teraz pokryjemy takimi prostymi całą półpłaszczyznę 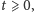 to problem jest rozwiązany, bo każdy punkt
to problem jest rozwiązany, bo każdy punkt  dla
dla  ma określoną wartość funkcji
ma określoną wartość funkcji  Jak to działa na konkretnym przykładzie, można zobaczyć na marginesie obok. Okazuje się jednak, że dla bardzo wielu warunków początkowych (nawet zupełnie gładkich) nie da się znaleźć rozwiązania ciągłego
Jak to działa na konkretnym przykładzie, można zobaczyć na marginesie obok. Okazuje się jednak, że dla bardzo wielu warunków początkowych (nawet zupełnie gładkich) nie da się znaleźć rozwiązania ciągłego  określonego dla wszystkich czasów
określonego dla wszystkich czasów 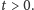 Tworzą się bowiem tzw. fale uderzeniowe jak na rysunku 3. W ten sposób widzimy, że spokrewnione z równaniem Naviera-Stokesa równanie, które zawiera podobny składnik nieliniowy, dla niektórych warunków początkowych zachowuje się dobrze, a dla innych warunków początkowych na pewno nie daje globalnych w czasie i gładkich rozwiązań (bez względu na to, czy
Tworzą się bowiem tzw. fale uderzeniowe jak na rysunku 3. W ten sposób widzimy, że spokrewnione z równaniem Naviera-Stokesa równanie, które zawiera podobny składnik nieliniowy, dla niektórych warunków początkowych zachowuje się dobrze, a dla innych warunków początkowych na pewno nie daje globalnych w czasie i gładkich rozwiązań (bez względu na to, czy  dla
dla 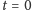 jest gładkie).
jest gładkie).
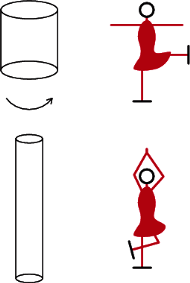
Rys. 4 Zwężanie wiru
Są też inne przyczyny, dla których składnik nieliniowy ma złą sławę: odwrotnie niż laplasjan pompuje energię ze skal większych do mniejszych, a ponadto z fizycznego punktu widzenia jest on związany z efektem zwężania wiru. Efekt ten polega na tym, że jeśli walec wodny wiruje wokół osi i jego promień ulega zmniejszeniu, to prędkość wirowania silnie wzrasta, tak jak w przypadku łyżwiarki robiącej piruet z otwartymi ramionami, która nagle ramiona zbliża do siebie (Rys. 4). Czy podobnie może dojść do wybuchu prędkości w przepływie płynu?
Niewidzialny rozgrywający
Wielu osobom wydaje się, że cały kłopot z równaniem Naviera-Stokesa polega właśnie na starciu składnika nieliniowego z laplasjanem. Część fizyków podejrzewa, że zmniejszając lepkość 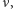 czyli osłabiając laplasjan względem składnika nieliniowego, można doprowadzić do wybuchów rozwiązań. Czy jednak tylko o starcie laplasjanu ze składnikiem nieliniowym tu chodzi?
czyli osłabiając laplasjan względem składnika nieliniowego, można doprowadzić do wybuchów rozwiązań. Czy jednak tylko o starcie laplasjanu ze składnikiem nieliniowym tu chodzi?
Problem w tym, że równanie z pominiętym gradientem ciśnienia:

i w konsekwencji z jednocześnie pominiętym warunkiem bezdywergencyjności pola  ma zupełnie dobre własności: rozwiązania są ograniczone, o ile tylko
ma zupełnie dobre własności: rozwiązania są ograniczone, o ile tylko  jest ograniczona! Wykazali to Andriej Kisieliow oraz Olga Ładyżeńska w 1957 r. W przypadku równania Naviera-Stokesa gradient ciśnienia pełni niejako rolę funkcji
jest ograniczona! Wykazali to Andriej Kisieliow oraz Olga Ładyżeńska w 1957 r. W przypadku równania Naviera-Stokesa gradient ciśnienia pełni niejako rolę funkcji 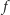 z równania badanego przez Kisieliowa i Ładyżeńską. Gdybyśmy zatem wiedzieli, że gradient ciśnienia nie wybucha, to moglibyśmy wnioskować, że
z równania badanego przez Kisieliowa i Ładyżeńską. Gdybyśmy zatem wiedzieli, że gradient ciśnienia nie wybucha, to moglibyśmy wnioskować, że  też nie
też nie 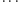 Niestety, nic takiego o ciśnieniu nie wiemy. Widać zatem, że o składniku
Niestety, nic takiego o ciśnieniu nie wiemy. Widać zatem, że o składniku 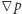 można mówić jak o kluczowej postaci równania Naviera-Stokesa. It is all about pressure... - jak mawia wielu matematyków zajmujących się tym tematem.
można mówić jak o kluczowej postaci równania Naviera-Stokesa. It is all about pressure... - jak mawia wielu matematyków zajmujących się tym tematem.
Dlaczego jednak ciśnienie nazwaliśmy postacią niewidzialną? Otóż gradient ciśnienia i prędkość  należą do wzajemnie prostopadłych przestrzeni funkcyjnych. Dla części Czytelników może to brzmieć dziwnie, że dwie funkcje są do siebie prostopadłe, ale jest to zupełnie sensowne uogólnienie pojęcia zwykłej prostopadłości wektorów: dwa wektory są prostopadłe, gdy ich iloczyn skalarny jest równy zeru, dwie funkcje są prostopadłe, gdy średnia ich iloczynu w przestrzeni jest równa zeru. To właśnie z powodu owej ortogonalności (prostopadłości) gradientu i funkcji z zerową dywergencją (tzn. pola bezźródłowego) w większości sformułowań równania Naviera-Stokesa spotykanych w fachowych artykułach ciśnienie po prostu znika, bo równanie rzutuje się od razu tylko na tę podprzestrzeń, w której "żyje" rozwiązanie
należą do wzajemnie prostopadłych przestrzeni funkcyjnych. Dla części Czytelników może to brzmieć dziwnie, że dwie funkcje są do siebie prostopadłe, ale jest to zupełnie sensowne uogólnienie pojęcia zwykłej prostopadłości wektorów: dwa wektory są prostopadłe, gdy ich iloczyn skalarny jest równy zeru, dwie funkcje są prostopadłe, gdy średnia ich iloczynu w przestrzeni jest równa zeru. To właśnie z powodu owej ortogonalności (prostopadłości) gradientu i funkcji z zerową dywergencją (tzn. pola bezźródłowego) w większości sformułowań równania Naviera-Stokesa spotykanych w fachowych artykułach ciśnienie po prostu znika, bo równanie rzutuje się od razu tylko na tę podprzestrzeń, w której "żyje" rozwiązanie 
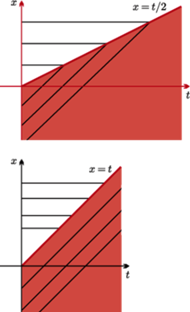
Rys. 5 Rozważmy równanie Burgersa z warunkiem początkowym 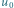 równym 1 dla
równym 1 dla  ujemnych i 0 dla
ujemnych i 0 dla  dodatnich. Linie, na których określamy wartość funkcji (zero lub jeden), przecinają się. Ale można zdefiniować słabe rozwiązanie - także za pomocą funkcji testowych. Okazuje się, że
dodatnich. Linie, na których określamy wartość funkcji (zero lub jeden), przecinają się. Ale można zdefiniować słabe rozwiązanie - także za pomocą funkcji testowych. Okazuje się, że  zdefiniowane jak na górnym rysunku (obszar zacieniowany to wartość
zdefiniowane jak na górnym rysunku (obszar zacieniowany to wartość  równa 1) wszystkie testy przechodzi, a to na rysunku dolnym - nie. Górne jest zatem słabym rozwiązaniem, a dolne nie jest. Widzimy też, że definicja słabego rozwiązania wyznacza w tym przypadku, jak porusza się fala uderzeniowa.
równa 1) wszystkie testy przechodzi, a to na rysunku dolnym - nie. Górne jest zatem słabym rozwiązaniem, a dolne nie jest. Widzimy też, że definicja słabego rozwiązania wyznacza w tym przypadku, jak porusza się fala uderzeniowa.
Słabe rozwiązania
W badaniach nad równaniem Naviera-Stokesa przełomowe znaczenie miała praca francuskiego matematyka Jeana Leraya z 1934 r. Leray pokazał, że dla każdego sensownego warunku początkowego 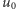 można skonstruować tzw. "słabe" rozwiązania
można skonstruować tzw. "słabe" rozwiązania  dla wszystkich czasów
dla wszystkich czasów 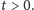 Co to znaczy, że rozwiązanie jest "w słabym sensie"? Mówiąc swobodnie, znaczy to, że spełnia ono pewną nieskończoną serię testów, które każde "prawdziwe", regularne rozwiązanie by spełniało. Może się jednak zdarzyć, że pewna funkcja wszystkie te testy przechodzi, a jednak nie spełnia równania w sensie zwykłym. Jest to sytuacja trochę podobna do zdawania matury: każdy w pełni dojrzały matematyk zaliczy serię wymaganych przez nią testów, ale nie jest prawdą, że każdy, kto maturę zaliczy, jest od razu dojrzałym matematykiem.
Co to znaczy, że rozwiązanie jest "w słabym sensie"? Mówiąc swobodnie, znaczy to, że spełnia ono pewną nieskończoną serię testów, które każde "prawdziwe", regularne rozwiązanie by spełniało. Może się jednak zdarzyć, że pewna funkcja wszystkie te testy przechodzi, a jednak nie spełnia równania w sensie zwykłym. Jest to sytuacja trochę podobna do zdawania matury: każdy w pełni dojrzały matematyk zaliczy serię wymaganych przez nią testów, ale nie jest prawdą, że każdy, kto maturę zaliczy, jest od razu dojrzałym matematykiem.
Spróbujmy dokładniej wytłumaczyć, jakie testy przechodzi słabe rozwiązanie określone na odcinku czasu 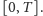 Standardowy test wygląda następująco. Bierzemy dowolną, ale bardzo gładką funkcję wektorową
Standardowy test wygląda następująco. Bierzemy dowolną, ale bardzo gładką funkcję wektorową  która znika przy brzegu
która znika przy brzegu 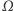 oraz znika dla czasów bliskich
oraz znika dla czasów bliskich  i
i 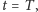 a także ma zerową dywergencję. Następnie mnożymy przez nią równanie (1), otrzymując:
a także ma zerową dywergencję. Następnie mnożymy przez nią równanie (1), otrzymując:
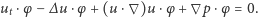
Dla każdego z czterech składników liczymy teraz jego średnią po całej czasoprzestrzeni. Suma tych czterech średnich też, oczywiście, musi być równa zeru. Kiedy jednak liczymy średnie, to pewne prawa rachunku całkowego (całkowanie przez części) pozwalają nam przerzucić pochodne na gładką funkcję testującą. To znaczy: gdyby 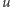 było prawdziwym gładkim rozwiązaniem, to obliczenie np. średniej iloczynu
było prawdziwym gładkim rozwiązaniem, to obliczenie np. średniej iloczynu 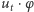 byłoby tym samym, co obliczenie średniej iloczynu
byłoby tym samym, co obliczenie średniej iloczynu 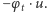 Ta ostatnia średnia istnieć może nawet wtedy, gdy samej funkcji
Ta ostatnia średnia istnieć może nawet wtedy, gdy samej funkcji  różniczkować się nie da. I na tym właśnie polega pomysł nieskończonej serii testów: pochodne zostają przerzucone na funkcję próbną, która jest na tyle gładka, że takie różniczkowania zniesie bez problemu, nawet gdyby nasze "słabe rozwiązanie" udźwignąć ich nijak nie mogło. Następnie sprawdzamy, czy suma średnich (obliczonych po odpowiednim przerzuceniu pochodnych na
różniczkować się nie da. I na tym właśnie polega pomysł nieskończonej serii testów: pochodne zostają przerzucone na funkcję próbną, która jest na tyle gładka, że takie różniczkowania zniesie bez problemu, nawet gdyby nasze "słabe rozwiązanie" udźwignąć ich nijak nie mogło. Następnie sprawdzamy, czy suma średnich (obliczonych po odpowiednim przerzuceniu pochodnych na 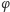 ) nadal jest równa zeru. Jeśli tak, to test jest zaliczony. Słabe rozwiązanie
) nadal jest równa zeru. Jeśli tak, to test jest zaliczony. Słabe rozwiązanie 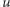 spełnia każdy taki test. Czy jednak można na nie z powrotem przerzucać pochodne? Gdyby tak było, to w konsekwencji
spełnia każdy taki test. Czy jednak można na nie z powrotem przerzucać pochodne? Gdyby tak było, to w konsekwencji  musiałoby być też rozwiązaniem klasycznym. Ale czy tak jest, nie wie nikt.
musiałoby być też rozwiązaniem klasycznym. Ale czy tak jest, nie wie nikt.
Trzy klasyczne wyniki
Skoro zapoznaliśmy się z grubsza z pojęciem słabego rozwiązania, to możemy teraz podać trzy najbardziej fundamentalne wyniki dotyczące równania Naviera-Stokesa. Obecnie wiemy, że:
- rozwiązania słabe istnieją globalnie w czasie, tzn. są określone dla wszystkich
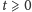 ; można je też tak skonstruować, że ich energia (czyli, z grubsza biorąc, średnia
; można je też tak skonstruować, że ich energia (czyli, z grubsza biorąc, średnia 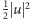 ) maleje w czasie, a warunek początkowy jest przyjmowany w tym sensie, że energia pola
) maleje w czasie, a warunek początkowy jest przyjmowany w tym sensie, że energia pola 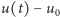 dąży do zera, gdy
dąży do zera, gdy 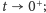 nie jest jednak obecnie wykluczone, że różne metody konstrukcji słabych rozwiązań prowadzą do różnych słabych rozwiązań dla tego samego
nie jest jednak obecnie wykluczone, że różne metody konstrukcji słabych rozwiązań prowadzą do różnych słabych rozwiązań dla tego samego 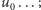
- rozwiązania klasyczne (czyli takie, które po prostu w zwykły sposób spełniają równanie) istnieją lokalnie w czasie: jeśli tylko warunek początkowy nie jest zbyt "dziki" (tzn. gdy średnia
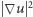 jest skończona), to przynajmniej na pewnym odcinku czasu
jest skończona), to przynajmniej na pewnym odcinku czasu 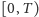 można skonstruować gładkie rozwiązanie;
można skonstruować gładkie rozwiązanie; - jeśli warunek początkowy jest bardzo mały (np. w tym sensie, że średnia
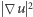 jest odpowiednio mała), to rozwiązania klasyczne istnieją globalnie w czasie (czyli dla każdego
jest odpowiednio mała), to rozwiązania klasyczne istnieją globalnie w czasie (czyli dla każdego 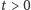 ).
).
Wiemy też, że rozwiązania klasyczne są zawsze jednoznaczne (nie można mieć dwóch różnych rozwiązań klasycznych dla tego samego 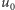 ).
).
Słoń Edrissa Titiego
Edriss Titi, jeden z bardziej znanych badaczy równania Naviera-Stokesa, zwykł mawiać, że równanie to jest jak słoń czy też mamut, którego ludzie chcą pokonać, ale wciąż nie potrafią. Zamiast więc mamuta w pełni zwyciężyć, dokonują różnych sztuczek: a to złapią go za ucho, a to pobujają się na ogonie, to znów ugodzą go w nogę. Metaforę Titiego należy, oczywiście, traktować z pewnym dystansem, ale faktem jednak jest, że w ciągu wielu lat badań udało się dokonać wielu matematycznych "sztuczek". Wykazano na przykład, że:
- jeśli dochodzi do wybuchu, to i tak zbiór czasów, w jakim słabe rozwiązanie wybucha, jest mały: dla dowolnego
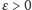 można go przykryć serią odcinków o długościach
można go przykryć serią odcinków o długościach  o tej własności, że
o tej własności, że 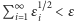 (czyli tzw. wymiar Hausdorffa zbioru czasów osobliwych nie jest większy od 1/2); wiedział to już w pewnej formie Leray w 1934 r.;
(czyli tzw. wymiar Hausdorffa zbioru czasów osobliwych nie jest większy od 1/2); wiedział to już w pewnej formie Leray w 1934 r.; - zbiór punktów w czasoprzestrzeni, w których być może dochodzi do wybuchu, też jest mały (jego wymiar Hausdorffa nie jest większy niż 1 - to wynik Caffarelliego, Kohna i Nirenberga z 1982 r. w oparciu o wcześniejsze pomysły Scheffera z lat 70.);
- danemu słabemu rozwiązaniu odpowiada sensowny zespół trajektorii cząstek (trajektorii Lagrange'a); to wynika z pracy Foiasa, Guillope i Temama z 1985 r.
Faktów podobnej wagi można podać jeszcze co najmniej kilkanaście. A jednak problem główny pozostaje otwarty i nie bardzo wiadomo, jak te częściowe wyniki nas do jego pokonania zbliżają 
Milion dolarów
Równanie Naviera-Stokesa opisujące przepływ w obszarze trójwymiarowym stało się w ostatnich latach dodatkowo sławne, bowiem zawarto je na liście tzw. siedmiu problemów milenijnych (wytypowanych jako najważniejsze problemy otwarte w matematyce). Żeby przemówić do wyobraźni osób spoza branży, ufundowano konkretną i łatwą do zrozumienia nagrodę w wysokości miliona dolarów za rozwiązanie któregokolwiek z tych siedmiu problemów. W ten sposób równanie Naviera-Stokesa stało się obecne w tzw. kulturze masowej, co prowadzi czasami do nieoczekiwanych efektów. Na przykład niedawno "eksperci" rozmaitych portali poinformowali opinię publiczną o "geniuszu z Kazachstanu", który "rozwiązał zagadkę za milion dolarów". Niestety, w dowodzie Mukhatarbaja Otelbajeva po kilku tygodniach znaleziono błąd. Było jednak dość emocjonująco: w poszukiwaniu pomyłki brało udział wielu matematyków, ostatecznie kontrprzykład (ulepszony potem przez Terrence'a Tao) został podany przez użytkownika o nicku "sup" na jednym z rosyjskojęzycznych portali matematycznych. Wydaje się obecnie, że dowodu Otelbajeva nie da się uratować. Tego rodzaju zdarzenia trafiają się od czasu do czasu, np. w roku 2006 Penny Smith ogłosiła, że ma dowód i nieostrożnie udzieliła na ten temat wywiadu dziennikarce Nature. Potem okazało się, że choć sama praca poświęcona równaniu Naviera-Stokesa nie zawierała bezpośrednio błędu, to jednak opierała się na poprzedniej błędnej pracy autorki.
Pomimo zatem tysięcy prac na ten temat, pomimo wysiłków setek matematyków problem regularności rozwiązań Naviera-Stokesa wciąż czeka na ostateczne rozstrzygnięcie. A przecież od momentu podania tych równań przez francuskiego inżyniera Claude-Louisa Naviera w 1822 roku i ich bardziej ścisłego wyprowadzenia przez George'a Gabriela Stokesa w 1845 roku minęło już całkiem dużo czasu...
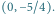 Mamy
Mamy 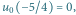 więc rysujemy z punktu
więc rysujemy z punktu 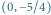 prostą o współczynniku kierunkowym zero. Na tej prostej wartość
prostą o współczynniku kierunkowym zero. Na tej prostej wartość  jest równa zeru.
jest równa zeru.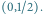 Mamy
Mamy 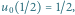 więc rysujemy z punktu
więc rysujemy z punktu 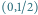 prostą o współczynniku kierunkowym
prostą o współczynniku kierunkowym 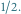 Na tej prostej wartość
Na tej prostej wartość  jest równa
jest równa 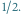
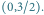 Mamy
Mamy 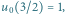 więc rysujemy prostą z punktu
więc rysujemy prostą z punktu 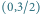 o współczynniku kierunkowym równym 1. Na tej prostej wartość
o współczynniku kierunkowym równym 1. Na tej prostej wartość  jest równa 1.
jest równa 1. Jak zatem określać rozwiązanie w spornych punktach? Gdzie ma przebiegać linia skoku (fala uderzeniowa)? I czy takie nieciągłe rozwiązania mają w ogóle sens?
Jak zatem określać rozwiązanie w spornych punktach? Gdzie ma przebiegać linia skoku (fala uderzeniowa)? I czy takie nieciągłe rozwiązania mają w ogóle sens?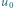 równym 1 dla
równym 1 dla  ujemnych i 0 dla
ujemnych i 0 dla  dodatnich. Linie, na których określamy wartość funkcji (zero lub jeden), przecinają się. Ale można zdefiniować słabe rozwiązanie - także za pomocą funkcji testowych. Okazuje się, że
dodatnich. Linie, na których określamy wartość funkcji (zero lub jeden), przecinają się. Ale można zdefiniować słabe rozwiązanie - także za pomocą funkcji testowych. Okazuje się, że  zdefiniowane jak na górnym rysunku (obszar zacieniowany to wartość
zdefiniowane jak na górnym rysunku (obszar zacieniowany to wartość  równa 1) wszystkie testy przechodzi, a to na rysunku dolnym - nie. Górne jest zatem słabym rozwiązaniem, a dolne nie jest. Widzimy też, że definicja słabego rozwiązania wyznacza w tym przypadku, jak porusza się fala uderzeniowa.
równa 1) wszystkie testy przechodzi, a to na rysunku dolnym - nie. Górne jest zatem słabym rozwiązaniem, a dolne nie jest. Widzimy też, że definicja słabego rozwiązania wyznacza w tym przypadku, jak porusza się fala uderzeniowa.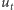 oznacza pochodną względem czasu, przez
oznacza pochodną względem czasu, przez 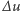 oznaczamy wektor
oznaczamy wektor 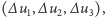 gdzie
gdzie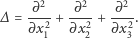
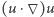 oznaczamy wektor, którego
oznaczamy wektor, którego 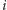 -ta współrzędna jest równa sumie
-ta współrzędna jest równa sumie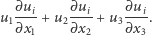
 jest równa zeru:
jest równa zeru: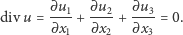
 bowiem ich iloczyn jest równy
bowiem ich iloczyn jest równy  a średnia
a średnia 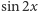 na
na 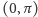 jest równa zeru.
jest równa zeru. bez brzegu, to jest w całej przestrzeni lub na kostce z periodycznymi warunkami brzegowymi. Oczywiście problem dotyczył przepływu w obszarze trójwymiarowym, bo problem przepływu w obszarze dwuwymiarowym został dawno już rozwiązany (nie ma wybuchów w wymiarze 2) przez Olgę Ładyżeńską.
bez brzegu, to jest w całej przestrzeni lub na kostce z periodycznymi warunkami brzegowymi. Oczywiście problem dotyczył przepływu w obszarze trójwymiarowym, bo problem przepływu w obszarze dwuwymiarowym został dawno już rozwiązany (nie ma wybuchów w wymiarze 2) przez Olgę Ładyżeńską.