Matematyka żonglowania
Żonglerka to starożytna sztuka, jej początki wydają się dorównywać wiekiem ludzkości, znane są np. rysunki żonglującej kobiety znalezione w egipskim grobowcu datowanym na XII wiek p.n.e. Wystarczy kilka kamieni i trochę praktyki, nie jest więc wcale zdumiewające, że ludzie zaczęli się tym zajmować bardzo dawno.
Jednakże dopiero bardzo niedawno zaczęto się interesować matematycznymi aspektami żonglowania. Pierwszy raz matematyczną notację dla wzorców żonglowania wprowadzono w latach 80. XX wieku niezależnie na Uniwersytecie Kalifornijskim w Santa Cruz, w Caltech i na uniwersytecie w Cambridge. Przedstawię tutaj krótki opis tego, jak matematycy mogą pomóc żonglerom w tworzeniu wzorców żonglerki i jak ta międzydziedzinowa współpraca może przydać się również matematykom.
Pierwszy krok to stworzenie schematycznego modelu po to, by móc o żonglowaniu mówić precyzyjnie. Załóżmy (na początek), że czas jest dyskretny, czyli jest ciągiem chwil 1, 2, 3, …, oraz że żongler ma dwie ręce, z których każda może trzymać w danej chwili co najwyżej jeden przedmiot (piłkę). Ręce poruszają się na zmianę, to znaczy jedna z nich łapie i rzuca piłkę w chwilach parzystych, a druga w nieparzystych.
Ciekawszą rzeczą są różne sposoby rzucenia piłki – my możemy to opisać
wyłącznie poprzez czas (liczbę chwil), który piłka spędza w powietrzu.
To znaczy rzut wysokości
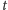 wykonany w chwili
wykonany w chwili
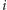 ląduje
w chwili
ląduje
w chwili
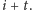 Zauważmy, że znaczy to, iż wszystkie rzuty
parzystej wysokości lądują w tej samej ręce, która je wyrzuciła, a te
o wysokości nieparzystej zmieniają rękę. Oznaczymy przez 0 pusty rzut, to
znaczy ręka wykonuje rzut 0 w chwili
Zauważmy, że znaczy to, iż wszystkie rzuty
parzystej wysokości lądują w tej samej ręce, która je wyrzuciła, a te
o wysokości nieparzystej zmieniają rękę. Oznaczymy przez 0 pusty rzut, to
znaczy ręka wykonuje rzut 0 w chwili
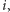 jeśli jest ona wolna
w chwili
jeśli jest ona wolna
w chwili
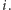
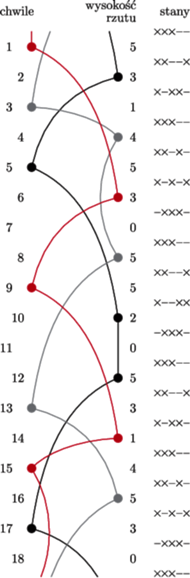
Rys. 1
Na rysunku 1 przedstawiony jest przykład sekwencji rzutów. Każda piłka jest identyfikowana przez swój kolor; dodatkowa informacja (stan) będzie przydatna w dalszej analizie. Zauważmy, że żongler używa trzech piłek.
Przedstawiona szczególna sekwencja będzie opisana tylko przez ciąg wykonanych rzutów, czyli – jak widać – 531453055205314530. Taką notację z angielskiego nazywamy siteswap. Żonglerzy zazwyczaj interesują się prostszymi sekwencjami aniżeli zaprezentowana tutaj. Szczególną uwagą darzone są sekwencje okresowe, w których skończony ciąg rzutów może być powtarzany w nieskończoność. Na przykład pierwszym wzorcem, którego uczy się większość ludzi, to ten z trzema piłkami, zwany kaskadą; odpowiada on ciągowi 33333….
Aby uniknąć powtarzania zbędnej informacji, zazwyczaj zapisujemy sekwencję okresową podając jedynie jej jeden okres, czyli w przypadku kaskady po prostu (3).
Matematyczny umysł może tu postawić wiele pytań. Czy wszystkie wzorce są poprawne? Jak liczba piłek zależy od wzorca? Ile wzorców istnieje przy pewnych ustalonych ograniczeniach (jak liczba piłek i maksymalna wysokość rzutu)?
Przyjrzyjmy się kilku podstawowym własnościom wzorców siteswap.
Definicja. Wzorzec
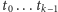 dla
dla
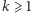 nazwiemy poprawnym wtedy i tylko wtedy,
gdy
nazwiemy poprawnym wtedy i tylko wtedy,
gdy
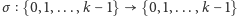 zdefiniowana
jako
zdefiniowana
jako
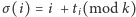 jest permutacją. Wszystkie wzorce dla
jest permutacją. Wszystkie wzorce dla
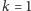 są poprawne; wzorzec
są poprawne; wzorzec
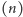 odpowiada kaskadzie
odpowiada kaskadzie
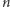 piłek.
piłek.
Ta definicja po prostu wyraża w inny sposób fakt, że dwie piłki nie mogą wylądować w tym samym momencie. Innymi słowy, różne rzuty we wzorcu muszą lądować w różnych chwilach.
Lemat. W poprawnym wzorcu dla
 piłek średnia wysokość
rzutów wynosi
piłek średnia wysokość
rzutów wynosi
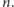
Dowód pozostawiam jako ćwiczenie-prezent dla Czytelnika lubiącego wyzwania.
Fakt opisany w lemacie może być użyty jako wstępny test na poprawność wzorca: jeśli średnia wysokość nie jest liczbą naturalną, to wzorzec nie może być poprawny.
Przykłady:
- (521) ma średnią 8/3, więc nie jest poprawnym wzorcem.
- (321) ma średnią 2, więc mógłby
opisywać wzorzec dla dwóch piłek; jednakże pierwszy warunek
nie jest spełniony:
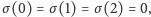 czyli wszystkie
piłki lądują w tym samym momencie.
czyli wszystkie
piłki lądują w tym samym momencie.
- (441), (531), (55500) są poprawnymi wzorcami dla trzech piłek. (6451), (7333), (71) są poprawnymi wzorcami dla czterech piłek.
Benoît Guerville udowodnił interesujący, nietrywialny fakt.
Twierdzenie (o reorganizacji). Każdy ciąg liczb naturalnych o średniej będącej liczbą naturalną można poprzestawiać tak, by przedstawiał poprawny wzorzec.
Powróćmy do rysunku 1. Chcę objaśnić to, co zostało umieszczone
w kolumnie stany. W każdej chwili możemy spojrzeć na wysokość danej
piłki, tzn. czas od danego momentu do jej wylądowania. Ponieważ dwie piłki
nigdy nie lądują w tej samej chwili, więc wszystkie wysokości będą różne.
Będziemy je zapisywać od lewej do prawej, znak
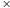 oznacza, że jest
piłka, a znak –, że jej nie ma. W szczególności, pierwszy symbol z lewej
strony odpowiada wysokości 0, czyli aktualnie aktywnej ręce. Opis stanu
kończy się na maksymalnej wysokości (w przykładzie to 5), więc opis
stanów jest skończony. Ograniczamy też wszystkie rzuty do tej maksymalnej
wysokości. To znaczy, że jeśli stan zaczyna się znakiem –, to aktualna ręka
jest pusta i następny rzut to 0. Przy czym, jeśli jest tam
oznacza, że jest
piłka, a znak –, że jej nie ma. W szczególności, pierwszy symbol z lewej
strony odpowiada wysokości 0, czyli aktualnie aktywnej ręce. Opis stanu
kończy się na maksymalnej wysokości (w przykładzie to 5), więc opis
stanów jest skończony. Ograniczamy też wszystkie rzuty do tej maksymalnej
wysokości. To znaczy, że jeśli stan zaczyna się znakiem –, to aktualna ręka
jest pusta i następny rzut to 0. Przy czym, jeśli jest tam
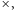 to piłka
może być rzucona na dowolną pozycję zaznaczoną –, czyli odpowiadającą
wolnemu miejscu. Maksymalny rzut jest zawsze dozwolony, gdyż odpowiada
wirtualnemu – za ostatnią pozycję. Wtedy wszystkie symbole są przesuwane
w lewo, co obrazuje upływającą jednostkę czasu. Używając stanów, zawsze
wiemy, jakie rzuty są dozwolone, co może być zilustrowane przez automat:
diagram stanów-przejść, taki jak na rysunku 2, gdzie są trzy piłki,
a maksymalna wysokość to 5.
to piłka
może być rzucona na dowolną pozycję zaznaczoną –, czyli odpowiadającą
wolnemu miejscu. Maksymalny rzut jest zawsze dozwolony, gdyż odpowiada
wirtualnemu – za ostatnią pozycję. Wtedy wszystkie symbole są przesuwane
w lewo, co obrazuje upływającą jednostkę czasu. Używając stanów, zawsze
wiemy, jakie rzuty są dozwolone, co może być zilustrowane przez automat:
diagram stanów-przejść, taki jak na rysunku 2, gdzie są trzy piłki,
a maksymalna wysokość to 5.
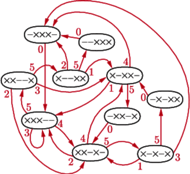
Rys. 2
A zatem poprawne ciągi to etykietowania ścieżek w tym automacie, a okresowe wzorce odpowiadają cyklom. To spojrzenie może być użyte do definiowania egzotycznych wzorców żonglowania i niektórzy artyści (na przykład firma Gandini Juggling) szeroko używają wzorców przy projektowaniu układów na swoje pokazy.
Zauważmy, że matematyczne rezultaty nigdzie nie wykorzystywały faktu, iż występują akurat dwie ręce. Wszystkie rozumowania będą wciąż poprawne dla większej liczby żonglujących „stron” (stóp, głowy, wielu osób, …). Badania nad wzorcami siteswap trwają, uogólnia się to pojęcie na wiele sposobów: dla czasu synchronicznego (wiele rąk rzuca w tym samym momencie), multipleksów (jedna ręka może rzucać wiele piłek naraz), ....
Rozważania te doprowadziły także do bardziej abstrakcyjnych badań naukowych, zostało opublikowanych wiele artykułów na ten temat, w większości o kombinatoryce wzorców. Interesujący jest fakt, że pewne pomysły rozwinięte podczas studiowania żonglowania były użyte w innych dziedzinach matematyki. Wiele artykułów, a czasem nawet prace doktorskie (np. Combinatorial aspects of juggling Anthony’ego Maysa) wskazują związki wzorców siteswap z nowatorskimi rozwiązaniami w matematyce. Nie ma takich rzeczy jak bezużyteczna matematyka: wzajemne powiązania często pojawiają się przy najbardziej niewinnych tematach!
Tłumaczył Wojciech CZERWIŃSKI