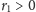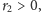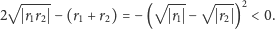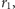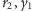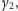Matematyka małżeństwa
Wydaje się, że nie ma rzeczy mniej logicznych niż uczucia. Czasami trwałe i szczęśliwe związki tworzą ludzie, o których mało kto by wcześniej powiedział, że są dla siebie stworzeni. Z drugiej strony, niejednokrotnie idealne, zdawałoby się, pary rozpadają się po pewnym czasie. W jaki sposób możemy więc przewidzieć dynamikę danego związku? Czy początkowy zachwyt drugą osobą będzie się umacniał, czy wręcz przeciwnie – zmieni się w niechęć? Na te pytania czasem trudno odpowiedzieć psychologom, a w zachowaniu partnerów niejednokrotnie trudno doszukać się logiki. Wydaje się, że angażowanie opartej na logice matematyki do tak trudnego i pozornie nieścisłego problemu jest skazane na porażkę. Okazuje się jednak, że „królowa nauk” nawet w takiej sytuacji jest w stanie wcisnąć swoje trzy grosze.

Opiszę tutaj badania przeprowadzone przez grupę amerykańskiego psychologa Johna Gottmana w latach osiemdziesiątych i dziewięćdziesiątych ubiegłego wieku. Pierwszy problem, przed którym stanęli badacze, to pytanie, w jaki sposób za pomocą liczb opisać emocje. W badaniach uczestniczyły 73 pary. Obserwowano ich zachowanie podczas rozmów na różne, budzące emocje tematy (takie jak pieniądze, teściowie, itp.) i zliczano zachowania „pozytywne” (np. humor, szczery uśmiech) i „negatywne” (np. krytyka, agresja). W ten sposób, po każdej takiej rozmowie otrzymywano liczbę będącą różnicą liczby zachowań „pozytywnych” i „negatywnych”, która w jakiś sposób opisywała stan emocjonalny każdego z partnerów.
Postaramy się teraz opisać zmiany stanów emocjonalnych partnerów za pomocą modelu matematycznego. Użyjemy modelu dyskretnego, czyli takiego, w którym stan procesu (tutaj stan emocjonalny każdego z partnerów) jest opisany tylko w pewnych oddalonych w czasie momentach. Dłuższą rozmowę warto arbitralnie podzielić na rundy i wydaje się, że kolejne wypowiedzi każdego z partnerów doskonale nadają się do tego, by po nich zapisać stan emocjonalny rozmówców.
Oznaczmy przez
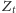 stan emocjonalny żony, a przez
stan emocjonalny żony, a przez
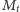 stan
emocjonalny męża po
stan
emocjonalny męża po
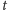 rundach. Przyjmijmy także, że to żona
rozpoczyna rozmowę. Stan emocjonalny partnerów będzie zmieniał się w czasie
i będzie opisany ciągiem liczb
rundach. Przyjmijmy także, że to żona
rozpoczyna rozmowę. Stan emocjonalny partnerów będzie zmieniał się w czasie
i będzie opisany ciągiem liczb
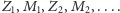 Przyjmijmy
jeszcze jedno założenie: stan emocjonalny partnera po kolejnej rundzie
zależy zarówno od jego aktualnego stanu emocjonalnego, jak i od stanu
emocjonalnego drugiego z partnerów. Niech ten wpływ opisują pewne funkcje
Przyjmijmy
jeszcze jedno założenie: stan emocjonalny partnera po kolejnej rundzie
zależy zarówno od jego aktualnego stanu emocjonalnego, jak i od stanu
emocjonalnego drugiego z partnerów. Niech ten wpływ opisują pewne funkcje
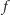 i
i
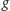 – ich postać ustalimy później. A zatem stan emocjonalny
partnerów opisujemy następującym układem równań:
– ich postać ustalimy później. A zatem stan emocjonalny
partnerów opisujemy następującym układem równań:
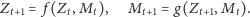
Z funkcji
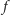 i
i
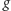 wydzielmy część niezależną od drugiego
partnera. Bez wpływów zewnętrznych nasze emocje zwykle ulegają wyciszeniu
i osiągamy pewien stan równowagi wewnętrznej (który może być różny
dla różnych osób – jedni są nastawieni bardziej pozytywnie do życia, inni
mniej). Ten składnik najłatwiej jest modelować przez równanie liniowe.
Przyjmijmy zatem, że gdyby obok nie było drugiego z partnerów, to stan
emocjonalny zmieniałby się zgodnie z równaniem liniowym
wydzielmy część niezależną od drugiego
partnera. Bez wpływów zewnętrznych nasze emocje zwykle ulegają wyciszeniu
i osiągamy pewien stan równowagi wewnętrznej (który może być różny
dla różnych osób – jedni są nastawieni bardziej pozytywnie do życia, inni
mniej). Ten składnik najłatwiej jest modelować przez równanie liniowe.
Przyjmijmy zatem, że gdyby obok nie było drugiego z partnerów, to stan
emocjonalny zmieniałby się zgodnie z równaniem liniowym
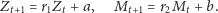 | (1) |
Przyjrzyjmy się zachowaniu rozwiązań jednego z powyższych równań. Mamy
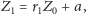 następnie
następnie
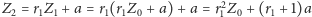 oraz
oraz
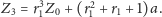 Stąd możemy wywnioskować
Stąd możemy wywnioskować
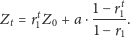
Jeśli
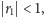 to wówczas ciąg
to wówczas ciąg
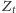 będzie zbliżał się do
będzie zbliżał się do
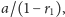 czyli stan emocjonalny osoby będzie się ustalał. Z drugiej strony,
jeśli
czyli stan emocjonalny osoby będzie się ustalał. Z drugiej strony,
jeśli
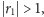 to ciąg nie będzie zbieżny i wartości
to ciąg nie będzie zbieżny i wartości
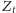 będą,
co do modułu, coraz większe. Taką osobę, której emocje „nakręcają” się
same z siebie, trudno uznać za zdrową psychicznie. Przyjmiemy zatem, że
będą,
co do modułu, coraz większe. Taką osobę, której emocje „nakręcają” się
same z siebie, trudno uznać za zdrową psychicznie. Przyjmiemy zatem, że
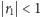 oraz
oraz
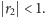
Do równań (1) dodajmy wpływ męża na żonę (i odwrotnie). Otrzymamy model
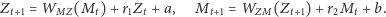 | (2) |
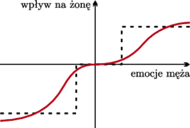
Przykładowa, „idealna” funkcja wpływu męża na żonę (kolorowa linia ciągła) i bardzo uproszczona (linia przerywana).
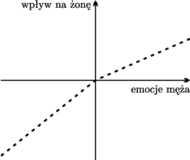
Funkcja wpływu męża na żonę użyta przez Gottmana.
Pozostaje nam w jakiś sposób zdefiniować funkcje wpływu męża na żonę
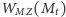 i żony na męża
i żony na męża
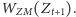 Spróbujmy
wyobrazić sobie, jak taka funkcja mogłaby wyglądać. Z odbiorem
pozytywnych sygnałów wysyłanych przez partnera jest podobnie jak
ze słodzeniem herbaty. Jeśli do herbaty wsypiemy za mało cukru, to
nie poczujemy, że posłodziliśmy napój. Z drugiej strony, jeśli wsypiemy
do jednej szklanki bardzo dużo cukru (powiedzmy pięć łyżeczek),
a do drugiej niewiele więcej (dajmy na to pięć i pół), to różnicy
w słodkości napojów w tych dwóch szklankach nie wyczujemy. Zatem
funkcja wpływu powinna zmieniać się wolno dla małych wartości emocji
(pozytywnych czy negatywnych), potem powinna zmieniać się szybciej,
a następnie tempo jej zmian znów powinno zwalniać. Przykład takiej funkcji
narysowaliśmy na rysunku obok kolorową linią ciągłą. Chociaż funkcja
opisująca odpowiedź na emocje negatywne powinna mieć podobny przebieg,
nie musi być ona odbiciem symetrycznym wpływu emocji pozytywnych. Łatwo
sobie wyobrazić osobę, która gwałtowniej reaguje na krytykę niż
na pochwały lub odwrotnie. Taka „idealna” funkcja ma jednak podstawową
wadę: jej kształt nie jest łatwy do opisania, szczególnie jeśli chcemy ją
dopasować do danych doświadczalnych (choć, oczywiście, nie jest to
niemożliwe). Konstruując model, staramy się uprościć opis sytuacji
na tyle, na ile to jest możliwe. Pewnym pomysłem na uproszczenie tej
„idealnej” funkcji jest rozpatrzenie funkcji kawałkami stałej (przerywana
linia na rysunku). Wówczas zakładamy, że do pewnego momentu
partnerzy nie reagują na sygnały drugiej strony, a następnie ich reakcja
jest stała.
Spróbujmy
wyobrazić sobie, jak taka funkcja mogłaby wyglądać. Z odbiorem
pozytywnych sygnałów wysyłanych przez partnera jest podobnie jak
ze słodzeniem herbaty. Jeśli do herbaty wsypiemy za mało cukru, to
nie poczujemy, że posłodziliśmy napój. Z drugiej strony, jeśli wsypiemy
do jednej szklanki bardzo dużo cukru (powiedzmy pięć łyżeczek),
a do drugiej niewiele więcej (dajmy na to pięć i pół), to różnicy
w słodkości napojów w tych dwóch szklankach nie wyczujemy. Zatem
funkcja wpływu powinna zmieniać się wolno dla małych wartości emocji
(pozytywnych czy negatywnych), potem powinna zmieniać się szybciej,
a następnie tempo jej zmian znów powinno zwalniać. Przykład takiej funkcji
narysowaliśmy na rysunku obok kolorową linią ciągłą. Chociaż funkcja
opisująca odpowiedź na emocje negatywne powinna mieć podobny przebieg,
nie musi być ona odbiciem symetrycznym wpływu emocji pozytywnych. Łatwo
sobie wyobrazić osobę, która gwałtowniej reaguje na krytykę niż
na pochwały lub odwrotnie. Taka „idealna” funkcja ma jednak podstawową
wadę: jej kształt nie jest łatwy do opisania, szczególnie jeśli chcemy ją
dopasować do danych doświadczalnych (choć, oczywiście, nie jest to
niemożliwe). Konstruując model, staramy się uprościć opis sytuacji
na tyle, na ile to jest możliwe. Pewnym pomysłem na uproszczenie tej
„idealnej” funkcji jest rozpatrzenie funkcji kawałkami stałej (przerywana
linia na rysunku). Wówczas zakładamy, że do pewnego momentu
partnerzy nie reagują na sygnały drugiej strony, a następnie ich reakcja
jest stała.
W swoich badaniach Gottman poszedł jednak inną drogą – przybliżył „idealną” funkcję przez funkcję kawałkami liniową (na dolnym obrazku). To podejście ma tę zaletę, że otrzymana funkcja jest ciągła i opisana jedynie przez dwa parametry: nachylenie prostej na prawo od zera i nachylenie prostej na lewo od zera. A zatem każda z funkcji wpływu będzie opisana dwoma parametrami i będą one dane wzorami:
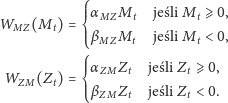
Zanim krótko omówię wyniki badań grupy Gottmana, zastanówmy się,
jakie własności matematyczne ma model (2), gdy funkcje wpływu są
kawałkami liniowe. Interesujące jest pytanie, czy istnieją punkty, w pobliżu
których wzajemne emocje mogą się ustabilizować, lub w których emocje
nie będą się zmieniać. Czyli jeśli
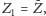 a
a
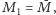 to
dla wszystkich
to
dla wszystkich
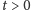 pozostanie prawdą, że
pozostanie prawdą, że
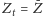 i
i
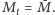 Punkt
Punkt
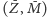 o takiej własności nazywa się
punktem stacjonarnym układu równań (2). Aby znaleźć punkty
stacjonarne wykorzystujemy to, że
o takiej własności nazywa się
punktem stacjonarnym układu równań (2). Aby znaleźć punkty
stacjonarne wykorzystujemy to, że
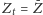 i
i
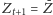 i podobnie
i podobnie
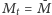 i
i
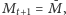 oraz równanie (2) i otrzymujemy układ
równań:
oraz równanie (2) i otrzymujemy układ
równań:
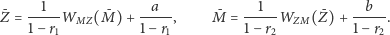 | (3) |
Ponieważ funkcje wpływu są kawałkami liniowe, to układ równań (3) jest
kawałkami liniowy i moglibyśmy go rozwiązać analitycznie. Jednak ciekawiej
i prościej będzie spojrzeć na rozwiązanie tego układu geometrycznie.
Zauważmy, że jeśli narysujemy prawe strony równań (3) na płaszczyźnie
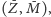 to ich przecięcia wyznaczą punkty stacjonarne. Czynniki
to ich przecięcia wyznaczą punkty stacjonarne. Czynniki
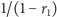 i
i
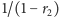 skalują funkcje wpływu (nachylenia
półprostych stają się mniejsze lub większe). Składnik
skalują funkcje wpływu (nachylenia
półprostych stają się mniejsze lub większe). Składnik
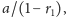 opisujący
stan, do którego zbliżają się emocje żony pozbawione wpływu jej męża,
przesuwa wykres tak, że przecina on oś
opisujący
stan, do którego zbliżają się emocje żony pozbawione wpływu jej męża,
przesuwa wykres tak, że przecina on oś
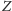 właśnie w tym
punkcie. Podobnie, składnik
właśnie w tym
punkcie. Podobnie, składnik
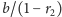 przesuwa wykres wzdłuż osi
przesuwa wykres wzdłuż osi
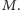 Skoro umiemy już wyznaczyć stany stacjonarne, to teraz
zbadajmy, jak zachowują się rozwiązania w okolicy tych stanów. Jeśli punkt
startowy znajduje się w pobliżu stanu stacjonarnego, to badamy, czy
rozwiązanie będzie się (w dłuższej perspektywie) do niego zbliżać
(mówimy wtedy, że stan stacjonarny jest asymptotycznie stabilny), czy
też oddali się od niego (powiemy wtedy, że punkt stacjonarny jest
niestabilny). W pobliżu stanu stacjonarnego układ równań (2) przyjmuje
postać
Skoro umiemy już wyznaczyć stany stacjonarne, to teraz
zbadajmy, jak zachowują się rozwiązania w okolicy tych stanów. Jeśli punkt
startowy znajduje się w pobliżu stanu stacjonarnego, to badamy, czy
rozwiązanie będzie się (w dłuższej perspektywie) do niego zbliżać
(mówimy wtedy, że stan stacjonarny jest asymptotycznie stabilny), czy
też oddali się od niego (powiemy wtedy, że punkt stacjonarny jest
niestabilny). W pobliżu stanu stacjonarnego układ równań (2) przyjmuje
postać
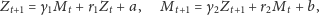 | (4) |
gdzie
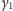 jest równe
jest równe
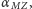 jeśli
jeśli
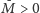 i
i
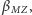 jeśli
jeśli
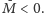 Podobnie,
Podobnie,
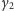 jest równe
jest równe
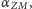 jeśli
jeśli
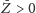 i
i
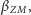 jeśli
jeśli
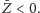 Żeby zobaczyć, co się dzieje w pobliżu stanu
stacjonarnego, wprowadzimy nowe zmienne
Żeby zobaczyć, co się dzieje w pobliżu stanu
stacjonarnego, wprowadzimy nowe zmienne
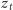 i
i
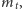 opisujące
odchylenie od stanu stacjonarnego. Mamy:
opisujące
odchylenie od stanu stacjonarnego. Mamy:
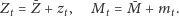
Wstawiając te równości do równania (4) i wykorzystując fakt, że spełnione są równania (3), otrzymujemy
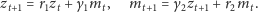 | (5) |
Wstawiając pierwsze równanie (5) do drugiego (by pozbyć się
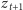 ),
otrzymujemy
),
otrzymujemy
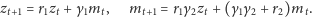 | (6) |
Poszukajmy teraz rozwiązań (6) postaci
 | (7) |
Wstawiając do (6) i przekształcając, otrzymujemy układ równań
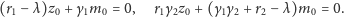
Aby ten układ miał niezerowe rozwiązania (a właściwie nieskończenie wiele
niezerowych rozwiązań), potrzebujemy, aby stosunek współczynnika przy
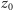 do współczynnika przy
do współczynnika przy
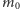 był taki sam w obu równaniach.
Zatem musi zachodzić
był taki sam w obu równaniach.
Zatem musi zachodzić
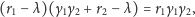
czyli
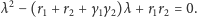 | (8) |
Ponieważ rozwiązania są postaci (7), to aby zbliżały się do zera (czyli
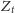 i
i
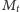 do
do
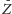 i
i
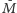 ), potrzebujemy, by rozwiązania
równania (8) były co do modułu mniejsze od jedynki.
), potrzebujemy, by rozwiązania
równania (8) były co do modułu mniejsze od jedynki.

Stwierdzenie 1. Niech
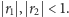 Jeżeli
Jeżeli
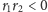 lub
lub
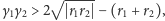 to rozwiązania
to rozwiązania
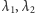 równania (8) są
rzeczywiste i jeśli dodatkowo
równania (8) są
rzeczywiste i jeśli dodatkowo
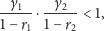 | (9) |
to
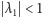 i
i
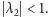
Dowód. Obliczmy najpierw wyróżnik równania kwadratowego (8)
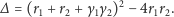
Jeśli
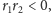 to oczywiście
to oczywiście
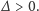 Podobnie, jeśli
Podobnie, jeśli
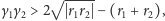 to
to
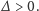 Aby przekonać się, że
stwierdzenie jest prawdziwe, musimy wykazać, że większy co do modułu
pierwiastek równania (8) jest mniejszy od
Aby przekonać się, że
stwierdzenie jest prawdziwe, musimy wykazać, że większy co do modułu
pierwiastek równania (8) jest mniejszy od
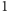 lub większy od
lub większy od
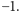 Przypuśćmy, że
Przypuśćmy, że
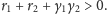 Wówczas większym
co do modułu pierwiastkiem jest ten z plusem przy
Wówczas większym
co do modułu pierwiastkiem jest ten z plusem przy
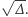 Zatem musimy
wykazać, że
Zatem musimy
wykazać, że
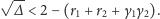 | (10) |
Zauważmy, że nierówność (9) możemy zapisać jako
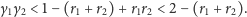
To dowodzi, że prawa strona nierówności (10) jest dodatnia i możemy nierówność podnieść stronami do kwadratu, co po skróceniu wyrazów sprowadzi ją do założonej nierówności (9).
Gottman ze swoim zespołem na podstawie obserwacji wyznaczył dla każdej
z par kąty nachylenia funkcji wpływu oraz wielkości
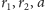 i
i
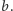 Następnie wyznaczono stany stacjonarne i ich stabilność. Okazało
się, że położenie stabilnego stanu stacjonarnego ma kluczowe znaczenie. Dla
par zakwalifikowanych wcześniej przez psychologów jako pary wysokiego
ryzyka (zagrożone rozpadem związku) przynajmniej jedna ze współrzędnych
stabilnego stanu stacjonarnego była ujemna, a druga była bliska zeru
lub także ujemna. Dla par niskiego ryzyka stabilny stan stacjonarny
znajdował się w pierwszej ćwiartce. Ponadto, wśród badanych osób
można było wyróżnić trzy podtypy różniące się nachyleniami funkcji
wpływu: wyraźnie dodatnie nachylenie obu liniowych części funkcji
wpływu (pozytywna reakcja na pozytywne emocje i negatywna reakcja
na negatywne emocje), wyraźnie dodatnie nachylenie prawej części
funkcji wpływu (pozytywna reakcja na pozytywne emocje) i bliskie zeru
nachylenie lewej części funkcji wpływu (słaba reakcja na negatywne
emocje) oraz bliskie zeru nachylenie prawej części funkcji wpływu (słaba
reakcja na pozytywne emocje) i wyraźnie dodatnie nachylenie lewej
części funkcji wpływu (negatywna reakcja na negatywne emocje). Pary
niskiego ryzyka miały podobne (tego samego typu) funkcje wpływu męża
i żony. Z drugiej strony, funkcje wpływu partnerów z par wysokiego
ryzyka zdają się pochodzić z różnych podtypów, czyli są do siebie
niedopasowane. To owocuje ujemnym stabilnym stanem stacjonarnym.
Wyniki tych badań sugerują hipotezę, że pary, których związek zdąża
do rozpadu, nie wypracowały schematu, jak mają na siebie wpływać,
a większość ich sporów dotyczy tego, w jaki sposób powinni się kłócić
czy rozmawiać ze sobą.
Następnie wyznaczono stany stacjonarne i ich stabilność. Okazało
się, że położenie stabilnego stanu stacjonarnego ma kluczowe znaczenie. Dla
par zakwalifikowanych wcześniej przez psychologów jako pary wysokiego
ryzyka (zagrożone rozpadem związku) przynajmniej jedna ze współrzędnych
stabilnego stanu stacjonarnego była ujemna, a druga była bliska zeru
lub także ujemna. Dla par niskiego ryzyka stabilny stan stacjonarny
znajdował się w pierwszej ćwiartce. Ponadto, wśród badanych osób
można było wyróżnić trzy podtypy różniące się nachyleniami funkcji
wpływu: wyraźnie dodatnie nachylenie obu liniowych części funkcji
wpływu (pozytywna reakcja na pozytywne emocje i negatywna reakcja
na negatywne emocje), wyraźnie dodatnie nachylenie prawej części
funkcji wpływu (pozytywna reakcja na pozytywne emocje) i bliskie zeru
nachylenie lewej części funkcji wpływu (słaba reakcja na negatywne
emocje) oraz bliskie zeru nachylenie prawej części funkcji wpływu (słaba
reakcja na pozytywne emocje) i wyraźnie dodatnie nachylenie lewej
części funkcji wpływu (negatywna reakcja na negatywne emocje). Pary
niskiego ryzyka miały podobne (tego samego typu) funkcje wpływu męża
i żony. Z drugiej strony, funkcje wpływu partnerów z par wysokiego
ryzyka zdają się pochodzić z różnych podtypów, czyli są do siebie
niedopasowane. To owocuje ujemnym stabilnym stanem stacjonarnym.
Wyniki tych badań sugerują hipotezę, że pary, których związek zdąża
do rozpadu, nie wypracowały schematu, jak mają na siebie wpływać,
a większość ich sporów dotyczy tego, w jaki sposób powinni się kłócić
czy rozmawiać ze sobą.