Najładniejsza choinka

Najładniejszą choinkę w życiu widziałem na Słowacji, w miejscowości Jasov. Jest tam klasztor założony w XII wieku, a obok niego rośnie sekwoja, a właściwie mamutowiec; drzewo to jest znacznie młodsze niż klasztor, bo ma tylko 180 lat. Uwagę patrzącego przyciąga pień, bardzo gruby przy ziemi i bardzo smukły na samej górze...
Kształt pnia (i wszystkich części każdego drzewa) to kwestia swoistej ekonomii; na drzewo działają rozmaite siły, które pień musi wytrzymać, i dlatego musi być dostatecznie gruby. Ale do zbudowania grubego pnia potrzeba bardzo dużo budulca, który trzeba wydobyć z gleby i z powietrza, i energii, otrzymywanej ze Słońca – to po tę energię drzewa „ścigają się do góry”. Im grubszy i wyższy jest pień, tym większe obciążenia musi wytrzymywać, co sprawia, że ten wyścig to nadzwyczaj trudna konkurencja. Mistrzami w niej są mamutowce.
Źródła sił działających na pień choinki to przede wszystkim grawitacja (ciężar samego pnia, gałęzi, igieł, szyszek, opadów atmosferycznych i siadających na gałęziach ptaków), wiatr, powodujący nie tylko zginanie, ale też skręcanie (choć momenty wywieranych przez poszczególne konary sił skręcających pień w znacznym stopniu się znoszą) i wreszcie bezwładność (ojczyzną mamutowców jest Kalifornia, obszar sejsmiczny). Wspomniana „ekonomia” ma na celu jak najlepsze wykorzystanie materiału, co sprowadza się do tego, by przy największych obciążeniach, na jakie pień bywa wystawiony, naprężenia w poszczególnych częściach pnia były bliskie wytrzymałości drewna, z którego pień jest zbudowany. W tym artykule chciałbym pokazać, jak z tak postawionego problemu „ekonomicznego” wynika rozwiązanie w postaci kształtu pnia. W tym celu zbuduję i zbadam pewien bardzo uproszczony model pnia mamutowca i działających na niego sił wiatru i grawitacji.

To, czy dany materiał wytrzyma obciążenie, zależy od tzw. trójosiowego stanu naprężeń. Na przykład, materiał rozciągany lub ściskany jednakowo we wszystkich kierunkach może wytrzymać większe naprężenie niż materiał rozciągany lub ściskany tylko w jednym kierunku. Ważne są też kierunkowe własności materiału: sztywność i wytrzymałość drewna rozciąganego wzdłuż włókien jest większa niż w kierunkach prostopadłych do włókien, co określa się mianem anizotropii. Na rozkład naprężeń w pniu ma wpływ zależność odkształceń od naprężeń. Dla prawie wszystkich ciał stałych, jeśli naprężenia są dostatecznie małe, zależność ta jest liniowa; jest to znane prawo Hooke’a. Jednak dla większych naprężeń (a zwłaszcza bliskich granicy wytrzymałości materiału) prawo to przestaje obowiązywać. Poza tym w różnych częściach pnia (zależnie od wieku drewna i zawartości wody) zależność ta może być różna. Tych wszystkich rzeczy nie weźmiemy dalej pod uwagę, ale budując model matematyczny czegokolwiek, zawsze należy pamiętać o najważniejszych pominiętych czynnikach (wszystkich nigdy nie znamy).
Przyjmiemy następujące nieprawdziwe (co nie znaczy od razu, że błędne) założenia: w każdym miejscu sztywność i wytrzymałość drewna jest taka sama (korę traktujemy jak drewno). Pień rośnie pionowo, a jego przekrój poziomy na każdej wysokości jest kołem, którego promień wolno zmienia się z wysokością. Grawitacja i zginanie przez wiatr powodują tylko ściskanie i rozciąganie włókien wzdłuż pnia, którego materiał spełnia prawo Hooke’a. Przy tych założeniach wspomniane przekroje pnia pozostają płaskie, tj. cząstki drewna położone na dowolnym poziomym przekroju pnia nieodkształconego po jego obciążeniu nadal znajdują się w jednej płaszczyźnie. Przyjmiemy ponadto, że średnice przekrojów po odkształceniu pnia pozostają niezmienione.
Wprowadzimy układ współrzędnych, którego oś
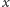 jest skierowana
pionowo do góry, oś
jest skierowana
pionowo do góry, oś
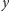 ma kierunek wiatru, który wieje poziomo,
a oś
ma kierunek wiatru, który wieje poziomo,
a oś
 jest do pozostałych dwóch osi prostopadła. Jeśli
jest do pozostałych dwóch osi prostopadła. Jeśli
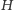 oznacza wysokość pnia, a funkcja
oznacza wysokość pnia, a funkcja
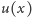 opisuje ugięcie (tj.
boczne przemieszczenie przekroju) pnia na wysokości
opisuje ugięcie (tj.
boczne przemieszczenie przekroju) pnia na wysokości
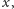 gdzie
gdzie
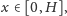 to dla niewielkich (z założenia) ugięć promień
okręgu ściśle stycznego do wygiętej osi pnia na wysokości
to dla niewielkich (z założenia) ugięć promień
okręgu ściśle stycznego do wygiętej osi pnia na wysokości
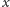 jest
w dobrym przybliżeniu równy
jest
w dobrym przybliżeniu równy
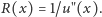 Jeśli w tym
miejscu przekrój pnia ma promień
Jeśli w tym
miejscu przekrój pnia ma promień
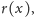 to maksymalne względne
zmiany długości włókien, spowodowane przez wygięcie pnia, są równe
to maksymalne względne
zmiany długości włókien, spowodowane przez wygięcie pnia, są równe
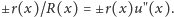 Wprowadźmy w płaszczyźnie przekroju
pnia lokalny układ współrzędnych
Wprowadźmy w płaszczyźnie przekroju
pnia lokalny układ współrzędnych
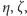 mający początek w środku
przekroju i taki, że oś
mający początek w środku
przekroju i taki, że oś
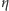 przed odkształceniem pnia ma kierunek
i zwrot osi
przed odkształceniem pnia ma kierunek
i zwrot osi
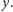 Względne odkształcenie włókna przecinającego
przekrój w punkcie
Względne odkształcenie włókna przecinającego
przekrój w punkcie
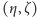 jest proporcjonalne do
jest proporcjonalne do
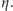 Z prawa
Hooke’a wynika, że także naprężenie włókna jest proporcjonalne
do
Z prawa
Hooke’a wynika, że także naprężenie włókna jest proporcjonalne
do
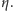 Naprężenia włókien spowodowane przez zginanie pnia
w rozważanym przekroju są zatem opisane przez funkcję
Naprężenia włókien spowodowane przez zginanie pnia
w rozważanym przekroju są zatem opisane przez funkcję
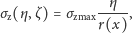
której wartość dodatnia oznacza, że włókno jest ściskane. Wypadkowy
moment siły dla naprężeń w przekroju pnia na wysokości
 możemy
wyrazić za pomocą całki po kole
możemy
wyrazić za pomocą całki po kole
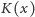 – przekroju pnia na tej
wysokości; całka ta jest objętością bryły pod wykresem funkcji
– przekroju pnia na tej
wysokości; całka ta jest objętością bryły pod wykresem funkcji
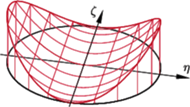
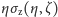 (Rys. 1), a oblicza się ją tak:
(Rys. 1), a oblicza się ją tak:
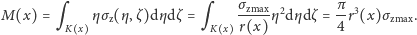
Z otrzymanego wyżej wzoru wynika, że wytrzymałość pnia na zginanie jest proporcjonalna do trzeciej potęgi promienia przekroju. Podobna zależność wytrzymałości od wielkości przekroju ma miejsce również dla belek, których przekroje mają kształt inny niż koło.
Rys. 1
Rys. 2

Rys. 3
Rys. 4
Pomińmy chwilowo naprężenia spowodowane przez grawitację, aby znaleźć
optymalny kształt pnia ze względu na wytrzymałość na podmuchy wiatru. Siła
parcia powietrza na gałąź drzewa zależy od wielkości i kształtu gałęzi i od
prędkości wiatru, przy czym dla przepływu turbulentnego, z jakim mamy tu do
czynienia, jest proporcjonalna do kwadratu prędkości wiatru. Sprawę
komplikuje fakt, że prędkość wiatru nie tylko zmienia się w czasie, ale
również zależy od wysokości – zwykle rośnie wraz z odległością od
ziemi. Ponieważ górne gałęzie są znacznie krótsze od tych położonych
niżej, gdzie prędkość wiatru jest mniejsza, wydaje się, że można (przy
braku lepszych informacji) zobaczyć, co wyjdzie, jeśli założymy, że siła
parcia wiatru na jednostkę długości (wysokości) pnia jest stała wzdłuż pnia.
Oznaczmy tę stałą symbolem
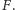 Wtedy moment siły wiatru zginającej
pień na wysokości
Wtedy moment siły wiatru zginającej
pień na wysokości
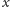 jest równy
jest równy
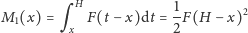
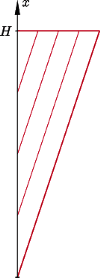
(ta całka jest polem trójkąta, który ma wierzchołek na wysokości
 i przeciwległy bok na wysokości
i przeciwległy bok na wysokości
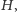 Rys. 2). Moment ten jest
wypadkowym momentem sił ściskających i rozciągających włókna
przekroju:
Rys. 2). Moment ten jest
wypadkowym momentem sił ściskających i rozciągających włókna
przekroju:
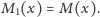 Mamy stąd równanie, które wiąże stałą
Mamy stąd równanie, które wiąże stałą
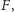 promień przekroju
promień przekroju
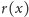 i maksymalne naprężenie
spowodowane przez zginanie
i maksymalne naprężenie
spowodowane przez zginanie
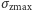 :
:
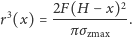 | (*) |
Jeśli założymy, że maksymalne naprężenie spowodowane przez zginanie ma
być takie samo na każdej wysokości, to funkcja opisująca promień
przekroju będzie mieć postać
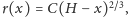 ze stałą
ze stałą
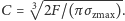 Zobaczmy wykres (Rys. 3): pień mamutowca tak nie
wygląda.
Zobaczmy wykres (Rys. 3): pień mamutowca tak nie
wygląda.
Rozważmy teraz grawitację. Oprócz ciężaru pnia musimy przy tym
uwzględnić ciężar gałęzi. W tym celu przyjmiemy kolejne nie całkiem
prawdziwe założenie, że rozkład ciężaru gałęzi wyrastających z pnia na
wysokości
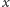 jest proporcjonalny do pola przekroju pnia na tej
wysokości. Przy tym założeniu siła ściskająca pień na wysokości
jest proporcjonalny do pola przekroju pnia na tej
wysokości. Przy tym założeniu siła ściskająca pień na wysokości
 jest równa
jest równa
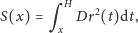 | (**) |
gdzie
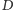 jest pewną stałą (siła ta jest więc proporcjonalna do objętości
części pnia powyżej poziomu
jest pewną stałą (siła ta jest więc proporcjonalna do objętości
części pnia powyżej poziomu
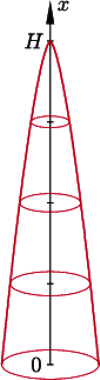
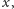 Rys. 4). Zgodnie z założeniami
modelu siła ta powoduje równomierne naprężenie
Rys. 4). Zgodnie z założeniami
modelu siła ta powoduje równomierne naprężenie
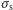 w całym
przekroju, musi ono zatem być równe
w całym
przekroju, musi ono zatem być równe
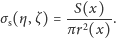 | (***) |
Naprężenia spowodowane ściskaniem i zginaniem pnia dodają się, zatem
skrajne naprężenia (odpowiednio we włóknach rozciąganych i ściskanych) to
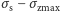 i
i
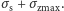 Aby pień wytrzymał obciążenie, oba te
naprężenia muszą leżeć w przedziale ograniczonym przez wytrzymałości
drewna na rozciąganie i ściskanie wzdłuż włókien. Zwrot siły grawitacji
sprawia, że maksymalne naprężenie ściskające ma większą wartość
bezwzględną niż rozciągające, dlatego (choć wytrzymałość drewna
na ściskanie może być większa niż na rozciąganie) zajmiemy się
ściskaniem: chcemy, aby przy najsilniejszym wietrze, na jaki drzewo jest
przygotowane, maksymalne naprężenie ściskające w każdym poziomym
przekroju pnia było stałe, równe maksymalnej wytrzymałości drewna na
ściskanie, którą oznaczymy symbolem
Aby pień wytrzymał obciążenie, oba te
naprężenia muszą leżeć w przedziale ograniczonym przez wytrzymałości
drewna na rozciąganie i ściskanie wzdłuż włókien. Zwrot siły grawitacji
sprawia, że maksymalne naprężenie ściskające ma większą wartość
bezwzględną niż rozciągające, dlatego (choć wytrzymałość drewna
na ściskanie może być większa niż na rozciąganie) zajmiemy się
ściskaniem: chcemy, aby przy najsilniejszym wietrze, na jaki drzewo jest
przygotowane, maksymalne naprężenie ściskające w każdym poziomym
przekroju pnia było stałe, równe maksymalnej wytrzymałości drewna na
ściskanie, którą oznaczymy symbolem
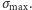 Zatem, na podstawie
Zatem, na podstawie
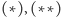 i
i
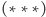 mamy
mamy
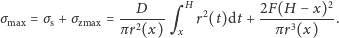 | (****) |
Dla wygody przekształcimy to równanie całkowe. Strony równości
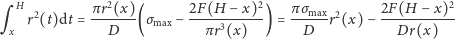
różniczkujemy względem
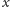 :
:
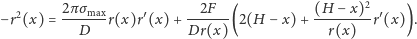
Po uporządkowaniu dostajemy stąd równanie różniczkowe zwyczajne
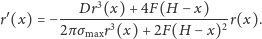
Właśnie ono jest matematycznym modelem pnia. Jako że bez dobrej nazwy niepodobna dziś odnieść sukces, nazwałem je Równaniem Mamutowca Kiciaka, w skrócie RóMaK (gdyby w wyprowadzeniu nie było tylu uproszczeń i wątpliwych założeń, nie zawahałbym się nazwać go Równaniem Prawdziwego Mamutowca).
RóMaK przepiszemy w postaci
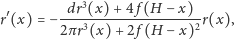
w której
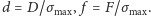 W ten sposób zmniejszyliśmy liczbę
parametrów. Poszukiwane rozwiązania spełniają warunek
W ten sposób zmniejszyliśmy liczbę
parametrów. Poszukiwane rozwiązania spełniają warunek
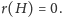 Niestety,
nie nadaje się on na warunek początkowy – poszukujemy rozwiązań dodatnich
w przedziale
Niestety,
nie nadaje się on na warunek początkowy – poszukujemy rozwiązań dodatnich
w przedziale
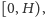 a funkcja zerowa spełnia RóMaK i ten
warunek. Polecam uwadze Czytelników sprawdzenie (za pomocą reguły de
l’Hôspitala), że dla
a funkcja zerowa spełnia RóMaK i ten
warunek. Polecam uwadze Czytelników sprawdzenie (za pomocą reguły de
l’Hôspitala), że dla
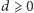 i
i
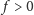 rozwiązanie niezerowe
w otoczeniu
rozwiązanie niezerowe
w otoczeniu
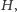 takie że
takie że
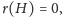 musi mieć w otoczeniu
musi mieć w otoczeniu
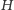 nieograniczoną pochodną; taką osobliwość ma np. znaleziona
wcześniej funkcja
nieograniczoną pochodną; taką osobliwość ma np. znaleziona
wcześniej funkcja
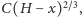 spełniająca RóMaK z parametrem
spełniająca RóMaK z parametrem
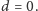 Jeśli
Jeśli
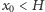 i
i
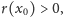 to funkcja
to funkcja
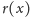 jest
dodatnia (i malejąca) w przedziale
jest
dodatnia (i malejąca) w przedziale
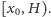
Będziemy poszukiwać rozwiązań numerycznie, przez rozwiązanie
zagadnienia początkowego dla RóMaK, przyjmując warunek początkowy
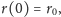 gdzie
gdzie
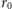 oznacza promień przekroju pnia przy ziemi.
Parametry
oznacza promień przekroju pnia przy ziemi.
Parametry
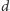 i
i
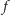 należy dobrać tak, aby funkcja
należy dobrać tak, aby funkcja
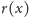 jak
najlepiej opisywała kształt pnia. W tym szaleństwie jest metoda: jeśli to się
uda, to, być może, dowiemy się czegoś o wartościach tych parametrów bez
mierzenia ich (co mogłoby być bardzo trudne).
jak
najlepiej opisywała kształt pnia. W tym szaleństwie jest metoda: jeśli to się
uda, to, być może, dowiemy się czegoś o wartościach tych parametrów bez
mierzenia ich (co mogłoby być bardzo trudne).
Aby numerycznie rozwiązywać RóMaK, możemy podzielić przedział
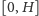 na
na
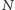 części, każda o długości
części, każda o długości
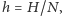 a następnie,
mając dane
a następnie,
mając dane
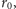 obliczać kolejno, dla
obliczać kolejno, dla
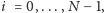
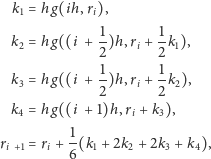
gdzie
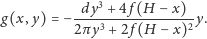
Jest to tzw. metoda Rungego–Kutty czwartego rzędu. Określa ona ciąg liczb
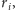 przybliżających wartości funkcji
przybliżających wartości funkcji
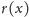 w punktach
w punktach
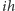 z dokładnością aż nadto wystarczającą w tym zastosowaniu.
z dokładnością aż nadto wystarczającą w tym zastosowaniu.

Rys. 5
Jak wybierać parametry
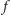 i
i
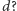 Nie są one niezależne. Oznaczmy
wielkości pomocnicze:
Nie są one niezależne. Oznaczmy
wielkości pomocnicze:
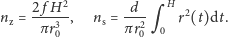
Na podstawie
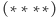 musi być
musi być
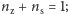 wielkości te
określają udziały naprężeń powodowanych przez zginanie i ściskanie
w maksymalnym naprężeniu w przekroju pnia przy ziemi. Mając dane
wielkości te
określają udziały naprężeń powodowanych przez zginanie i ściskanie
w maksymalnym naprężeniu w przekroju pnia przy ziemi. Mając dane
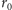 i
i
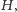 możemy wybrać
możemy wybrać
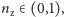 obliczyć
obliczyć
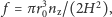 a następnie, rozwiązując RóMaK dla różnych
wartości parametru
a następnie, rozwiązując RóMaK dla różnych
wartości parametru
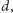 znaleźć taką jego wartość, aby równość
znaleźć taką jego wartość, aby równość
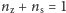 była spełniona. Mamy tu równanie nieliniowe z niewiadomą
była spełniona. Mamy tu równanie nieliniowe z niewiadomą
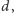 które można rozwiązać np. metodą bisekcji. Obliczając
które można rozwiązać np. metodą bisekcji. Obliczając
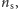 możemy posłużyć się wzorem przybliżonym
możemy posłużyć się wzorem przybliżonym
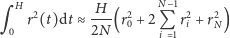
(jest to tzw. złożona kwadratura trapezów).
Pora zatrudnić do obliczeń komputer. Na podstawie zdjęć oceniłem
wysokość drzewa na 35 m. Przy ziemi pień ma średnicę około
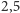 m, ale ponieważ okazało się, że model nie jest w stanie
odtworzyć zgrubienia pnia na samym dole (o czym dalej), przyjąłem
promień
m, ale ponieważ okazało się, że model nie jest w stanie
odtworzyć zgrubienia pnia na samym dole (o czym dalej), przyjąłem
promień
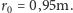 Wyniki obliczeń z
Wyniki obliczeń z
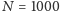 dla kilku
wartości parametru
dla kilku
wartości parametru
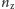 przedstawiają wykresy na rysunku 5 i tabelka:
przedstawiają wykresy na rysunku 5 i tabelka:
![| | | −1
--nz--|-ns--|- f-[m]---|d-[m--]-
0,05 |0,95 |5,49⋅10−5 |0,3722
0,1 |0,9 |1,10 ⋅10−4 |0,3084
0,2 |0,8 |2,19 ⋅10−4 |0,2371
| | −4 |
0,4 |0,6 |4,39⋅10 |0,1528](/math/temat/matematyka/zastosowania/2013/03/29/Najladniejsza_choinka/5x-914f222d3e2616c594c2b2f71f4e7384dbc6bf3d-dm-33,33,33-FF,FF,FF.gif)
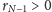 i
i
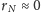 (jeśli
(jeśli
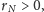 to parametr
to parametr
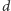 ma za małą wartość). Wydaje się, że
najlepsza zgodność z tym, co widać na zdjęciach ma miejsce, gdy
ma za małą wartość). Wydaje się, że
najlepsza zgodność z tym, co widać na zdjęciach ma miejsce, gdy
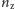 jest bliskie
jest bliskie
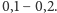 Sugeruje to, że naprężenia spowodowane
przez grawitację osiągają na dole pnia około 80–90% wytrzymałości drewna,
a pozostałe 10–20% to zapas na wypadek silnego wiatru. Na dużych
wysokościach dominują naprężenia powodowane przez zginanie.
Sugeruje to, że naprężenia spowodowane
przez grawitację osiągają na dole pnia około 80–90% wytrzymałości drewna,
a pozostałe 10–20% to zapas na wypadek silnego wiatru. Na dużych
wysokościach dominują naprężenia powodowane przez zginanie.
* * *
Wymyślając założenia i wyprowadzając z nich RóMaK, nie wiedziałem, co
z tego wyjdzie. Wyszło nieźle; „nie wyszło” tylko zgrubienie pnia tuż przy
ziemi. To oznacza, że założenia nie opisują poprawnie zjawisk zachodzących
w tym miejscu pnia. Warto więc jeszcze raz zastanowić się nad nimi. Kora,
która w dolnej części pnia jest bardzo gruba, nie przenosi obciążeń tak samo
jak drewno, a przekroje pnia nie są okrągłe i po obciążeniu nie pozostają
płaskie. Drzewa nie rosną idealnie pionowo i nawet niewielkie odchylenie od
pionu (rzędu
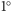 ) może bardzo zmienić rozkład naprężeń. Można też
zakwestionować podstawowe założenie, że maksymalne naprężenie na
każdej wysokości jest takie samo. Skutki ewentualnego złamania pnia dla
drzewa byłyby tym poważniejsze, im niżej by to nastąpiło – gdyby odłamał się
tylko czubek, to drzewo nadal mogłoby żyć i wytwarzać nasiona. Z tego
powodu prawdziwy pień może być na dole dodatkowo wzmocniony, czyli
grubszy, niż to wynika z modelu. Niemniej można dobrać parametry
modelu tak, aby funkcja
) może bardzo zmienić rozkład naprężeń. Można też
zakwestionować podstawowe założenie, że maksymalne naprężenie na
każdej wysokości jest takie samo. Skutki ewentualnego złamania pnia dla
drzewa byłyby tym poważniejsze, im niżej by to nastąpiło – gdyby odłamał się
tylko czubek, to drzewo nadal mogłoby żyć i wytwarzać nasiona. Z tego
powodu prawdziwy pień może być na dole dodatkowo wzmocniony, czyli
grubszy, niż to wynika z modelu. Niemniej można dobrać parametry
modelu tak, aby funkcja
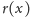 spełniająca RóMaK całkiem dobrze
opisywała kształt prawie całego pnia mamutowca. Ale kto chce, może
uznać, że podobieństwo otrzymanego wyniku do choinki z Jasova
jest słabe, a to, co ten model opisuje, to nie żaden mamutowiec, tylko
lipa.
spełniająca RóMaK całkiem dobrze
opisywała kształt prawie całego pnia mamutowca. Ale kto chce, może
uznać, że podobieństwo otrzymanego wyniku do choinki z Jasova
jest słabe, a to, co ten model opisuje, to nie żaden mamutowiec, tylko
lipa.
Mamutowiec z Jasowa
Klasztor w Jasovie od swego powstania w XII wieku był wielokrotnie przebudowywany; obecnie zespół klasztorny jest barokowy. W parku obok klasztoru rośnie mamutowiec olbrzymi (Sequoiadendron giganteum), największe drzewo tego gatunku na Słowacji. Ma ono 180 lat, 47.7 m wysokości i obwód pnia 7.42 m na wysokości 1.3 m.
Obok dużego mamutowca w Jasovie rosną dwa mniejsze; kiedyś będą wygladać podobnie, jak ten duży.
Mamutowiec z Tornanadaska
Kilkadziesiąt kilometrów od Jasova, w miejscowości Tornanadaska na Węgrzech, jest park, w którym rośnie inny wielki mamutowiec, też wart zobaczenia.








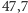 m
i obwód
m
i obwód
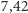 m na wysokości
m na wysokości
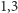 m.
m.