Epidemie
Wzór Bayesa a świńska grypa
Myślenie racjonalne
W połowie XVI wieku w pracach Cardano pojawiło się prawdopodobieństwo zdefiniowane jako proporcja – czyli iloraz – liczby zdarzeń sprzyjających zajściu badanego zdarzenia do liczby wszystkich możliwych zdarzeń elementarnych (tych, które mogą wystąpić w danym doświadczeniu). Pojęcie to rozwinięte zostało w XVII wieku w pracach Bernoulliego, Fermata i Pascala, a później było badane przez Laplace’a. Wtedy też dla oszacowania możliwości wygranych w grach losowych zaczęto wyznaczać prawdopodobieństwa i wielkości nazywane dziś wartościami oczekiwanymi zmiennych losowych. Do czasu pojawienia się w połowie XIX wieku teorii użyteczności Gossena szacowanie możliwości było traktowane jako najbardziej prawidłowy, pod względem naukowym, sposób racjonalnego rozwiązywania problemu wyboru w warunkach ryzyka. Tak pojmowana racjonalność przyjmuje również, że rozpatrując możliwość wystąpienia przyczyny, gdy zaistniał pewien skutek, powinniśmy wykorzystywać wzór Bayesa.
Badania przesiewowe, myślenie codzienne i rachunki
Grypa jest niebezpieczna, a skoro istnieją testy wykrywające wirusa, to czy nie warto zrobić powszechnych badań na jego obecność? Badanie przesiewowe to w medycynie rodzaj powszechnego badania, które wykonuje się w populacji lub tylko w tzw. grupach wysokiego ryzyka. Celem badania jest wykrycie choroby, ustalenie liczby lub frakcji chorych i umożliwienie zastosowania odpowiedniej terapii. W przypadku pozytywnego wyniku badania przesiewowego choroba musi być potwierdzona innymi metodami diagnostycznymi. Oczywiście, badania są obarczone błędem. Zarzuca się im ponadto „uspokojenie” pacjentów z ujemnym wynikiem testu, mimo że tak naprawdę są chorzy. Testy używane w badaniach powinny wykazywać się wysoką dokładnością. Gdyby wykonać badanie przesiewowe, to jak bardzo należy się przejmować w konkretnym przypadku jego wynikiem? W listopadzie 2009 r. przeprowadziłem badanie ankietowe 175 studentów uczelni ekonomicznej. Zadałem im pytanie jak poniżej.
W Polsce coraz więcej mówi się o tzw. świńskiej grypie. Robione są testy potwierdzające obecność wirusa A/H1N1. Testy te są bardzo dokładne. Pomyłka zachodzi raz na 1000 razy. Załóżmy, że w Polsce, która ma 38 mln mieszkańców, jest 200 osób chorych na świńską grypę (dotychczas łączna liczba takich przypadków wynosiła 171). Wybrano losowo jedną osobę. Test wykrył obecność wirusa A/H1N1. Jak oceniasz prawdopodobieństwo, że ta osoba jest rzeczywiście chora?
Czy jest to raczej mało prawdopodobne:
- 1*
- poniżej 0,01,
- 2*
- między 0,01 a 0,1,
- 3*
- między 0,1 a 0,5,
czy raczej bardzo prawdopodobne
- 4*
- między 0,5 a 0,7,
- 5*
- między 0,7 a 0,9,
- 6*
- powyżej 0,9?
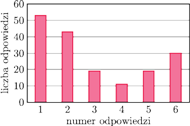
Liczba twierdzących odpowiedzi dla poszczególnych punktów była następująca: 1* 53, 2* 43, 3* 19, 4* 11, 5* 19, 6* 30, co dla zobrazowania wygodnie jest przedstawić na wykresie.
Widać tu preferowanie odpowiedzi skrajnych (1* + 6*) – łącznie ponad 47%. Odpowiedź pierwszą wybrało 30% ankietowanych i zbliżoną odpowiedź drugą prawie 25%, co razem daje prawie 55% ankietowanych. Oznacza to, że wśród badanych mniej więcej co druga osoba uznała, że opisane zdarzenie jest mało prawdopodobne. Stosunkowo duży procent odpowiedzi 6* może świadczyć o tym, że ankietowani w odpowiedzi kierowali się jedynie wysoką wiarygodnością testu, lekceważąc informację statystyczną, mówiącą o tym, że niezmiernie małe jest prawdopodobieństwo spotkania osoby chorej. Czy taki rozkład odpowiedzi należy uznać za dziwny? Raczej nie. Wyniki eksperymentu zgadzają się z badaniami Tversky’ego oraz Tversky’ego i Kahnemana, na podstawie których badacze doszli do wniosku, że ludzie zazwyczaj nie kierują się w wyborach regułami wynikającymi z probabilistycznej natury zjawiska. O ile bez obliczeń jest w oczywisty sposób dość trudno podać w miarę dokładną liczbową ocenę prawdopodobieństwa, o tyle stwierdzenie, czy zdarzenie jest raczej mało prawdopodobne, czy raczej bardzo prawdopodobne, powinno być dokonane w przeważającej większości w sposób właściwy. W przeprowadzonym badaniu jest tak w stosunku 115:60. Oznacza to, że prawie co trzecia osoba diametralnie myliła się w ocenie – zaraz zobaczymy, jak bardzo.
Spróbujmy zatem pomyśleć o badaniach przesiewowych w kontekście rachunku prawdopodobieństwa, przechodząc do „racjonalnego” myślenia i wzoru Bayesa.
Załóżmy, że Polska ma 38 000 000 mieszkańców, z których 200 jest chorych na świńską grypę. Gdybyśmy wybrali losowo jedną osobę, to prawdopodobieństwo tego, że jest ona chora, wynosi 200/38000000, czyli w przybliżeniu 0,0000053. Oczywiście, prawdopodobieństwo tego, że nie jest chora, wynosi 1 – 0,0000053, czyli 0,9999947. Przyjmijmy, że test wykazał obecność wirusa. Zastanówmy się, jakie jest prawdopodobieństwo tego, że pacjent, u którego stwierdzono obecność wirusa, jest rzeczywiście chory.
Skutkiem w naszym doświadczeniu jest stwierdzenie, że pacjent jest chory.
Pytamy o prawdopodobieństwo, że istotnie tak jest. Oznaczając przez A
zdarzenie, że u pacjenta stwierdzono obecność wirusa A/H1N1, natomiast
przez
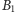 i
i
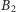 odpowiednio zdarzenia, że pacjent jest chory, oraz że
chory nie jest, zgodnie ze wzorem (**) otrzymujemy
odpowiednio zdarzenia, że pacjent jest chory, oraz że
chory nie jest, zgodnie ze wzorem (**) otrzymujemy
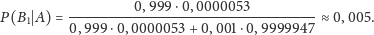 |
Powyższy wynik oznacza, że przy losowo wybranej osobie prawdopodobieństwo zdarzenia, że ma ona istotnie świńską grypę, mimo iż test na obecność wirusa dał rezultat pozytywny, jest małe. Dzieje się tak mimo wielkiej dokładności testu! Przypomnijmy, że w badaniu ankietowym odpowiedź tę (tzn. około 0,005) wybrało 30że wśród badanych mniej więcej co druga osoba podała wynik zbliżony do obliczonego ze wzoru Bayesa.
A już poza ankietą – jak byłoby, gdyby wynik testu był negatywny? Oznaczając przez A’ zdarzenie przeciwne do A (tzn. zdarzenie, że wynik testu jest negatywny), można obliczyć prawdopodobieństwo zdarzenia, że osoba jest chora, mimo że wynik testu jest negatywny. Otrzymujemy wtedy
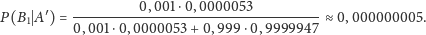 |
Oznacza to, że jeśli wynik testu jest negatywny, to osoba testowana prawie na pewno rzeczywiście nie ma świńskiej grypy.
Skąd wobec tego takie odpowiedzi ankietowanych? Dlaczego nie myślimy kategoriami prawdopodobieństwa? Ulegamy panice? Może trochę. Dlaczego tak jest? Być może dlatego, że lepiej spanikować i uciekać nawet przed mało prawdopodobnym nieszczęściem, niż skazać się na prawie niemożliwą, ale bardzo niekorzystną sytuację. Co ma robić społeczeństwo? Opinia publiczna wymusza czasem na politykach pewne decyzje. Bywa, że decyzji tych nie można zaliczyć do racjonalnych w sensie probabilistycznym. Dotychczas nie notuje się w mediach propozycji badań przesiewowych populacji. I bardzo dobrze, gdyż z rachunków wynika, że obarczone są wielkim błędem. Mimo dużej dokładności testu jego wynik, jakikolwiek by nie był, niesie ze sobą mało informacji o przyczynie. A koszty są niemałe.
Co robić, aby uniknąć groźnej choroby? Stosować się do takich samych zaleceń jak w przypadku innych chorób zakaźnych – unikać kontaktu z chorymi, stosować podstawowe zasady higieny i cieszyć się, że wirusy grypy dość szybko giną poza organizmem nosiciela lub chorego, a my mamy przed nimi naturalną obronę.
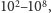 dlatego też przy określaniu
dokładności testu podaje się zazwyczaj logarytm liczby CFU/ml.
dlatego też przy określaniu
dokładności testu podaje się zazwyczaj logarytm liczby CFU/ml.