Epidemie
Wzór Bayesa a świńska grypa
Jesień 2009 roku. Na Ukrainie na początku listopada choruje na grypę już 200 000 osób. W kilkunastu przypadkach potwierdzono obecność wirusa A/H1N1, zwanego potocznie wirusem świńskiej grypy. W Polsce narasta niepokój. Potwierdzono obecność tego wirusa u kilku osób. Czy będziemy mieli epidemię?
Rząd uspokaja: liczba zachorowań na grypę nie rośnie. Ile z tych zachorowań dotyczy świńskiej grypy, dokładnie nie wiadomo, wykonuje się testy na obecność wirusa. Z danych Państwowego Zakładu Higieny wynika, że do 28 października 2009 roku odnotowano w Polsce 171 przypadków grypy typu A/H1N1. Główny Inspektorat Sanitarny w specjalnym komunikacie nakazuje natychmiastowe zgłaszanie się do lekarza wszystkim powracającym z zagranicy, którzy mają gorączkę, katar, ból gardła czy bóle mięśniowo-stawowe. Niepokoić zaczynają się także ci, którzy mają jakieś z tych objawów, mimo że za granicą nie byli. Proszą lekarzy o zlecenia na badanie krwi pod kątem obecności wirusa. Po wywiadzie lekarskim najczęściej okazuje się, że nie ma podstaw do takiego badania. Ale niepokój zostaje. Niektórzy decydują się zrobić badanie na swój koszt.
Test i prawdopodobieństwo
Metodą, która może być stosowana w celu wykrycia obecności wirusa, jest metoda Real-time PCR (ang. Polymerase Chain Reaction). Obecność materiału genetycznego wirusów jest uznawana za oznakę zakażenia. Wielu ekspertów zgodnie uznaje, że PCR to najlepsza metoda umożliwiająca monitoring chorych i mająca ogromną wartość diagnostyczną dla lekarza prowadzącego.
Niezależnie od tego, jak dobra jest metoda, mogą wystąpić przypadki błędu wynikającego, na przykład, z jakości materiału badawczego lub błędu operatora. Dla poprawnego działania testu PCR ważna jest koncentracja drobnoustrojów, liczona najczęściej w CFU/ml (ang. Colony Forming Units). Oczywiście, im koncentracja jest większa, tym większe jest prawdopodobieństwo, że przeprowadzony test da poprawny wynik. W książce wprowadzającej w tę technikę autorzy podają, że badania nad pierwotniakiem Cryptosporidium parvum pozwoliły uzyskać prawdopodobieństwo poprawnego wyniku rzędu 95% dla logarytmu dziesiętnego CFU/ml wynoszącego około 4,5. Przy koncentracji dziesięciokrotnie mniejszej prawdopodobieństwo wynosi około 75%, natomiast przy 100-krotnie mniejszej tylko około 30%. Trudno jest przy jednokrotnym stosowaniu metody uzyskać prawdopodobieństwo rzędu 99%, niezależnie od koncentracji. Oczywiście, przy wykonaniu większej liczby niezależnych testów prawdopodobieństwo wykrycia istniejącego w próbce pierwotniaka wzrasta. Pewne badania dotyczące komórek nowotworowych pokazują zgodność testu ze stanem faktycznym poniżej 95%. Dla wirusów ocena CFU lub podobna nie jest przeprowadzana, nie ma bowiem praktycznej możliwości stwierdzenia, jakie jest ich stężenie, gdyż mikroskopy nie zauważają tak małych organizmów, a wirusy nie tworzą kolonii. Gdyby bardzo optymistycznie przyjąć zgodność testu równą 99,9%, oznaczałoby to, że jest bardzo wysoka. Znaczy to też, że średnio test myliłby się raz na 1000 razy lub, innymi słowy, że wyznaczone częstościowo prawdopodobieństwo, iż test da wynik zgodny z rzeczywistością, wynosi 0,999.
Wzór Bayesa
Thomas Bayes, osiemnastowieczny matematyk angielski, zapewne nie przypuszczał, że podany przez niego wzór, nazywany dziś wzorem Bayesa, stosowany będzie powszechnie w statystyce i przyczyni się choćby do rozwoju współczesnego rynku finansowego (wycena instrumentów pochodnych). Wzór ten związany jest z pojęciem prawdopodobieństwa całkowitego, czyli prawdopodobieństwa wystąpienia zdarzenia, które może zajść po uprzednim zajściu pewnych warunków. Formalnie o prawdopodobieństwie całkowitym mówi poniższe twierdzenie.
Twierdzenie (o prawdopodobieństwie całkowitym). Jeżeli
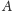 jest
dowolnym zdarzeniem,
jest
dowolnym zdarzeniem,
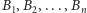 zaś są zdarzeniami
zaś są zdarzeniami
- a)
- wykluczającymi się parami, tzn.
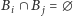 dla
dla
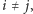
- b)
- o dodatnich prawdopodobieństwach zajścia, tzn.
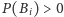 dla
dla
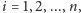
- c)
- takimi, że ich suma jest zdarzeniem pewnym, tzn.
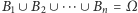 ,
,
to prawdopodobieństwo (nazywane całkowitym) zajścia zdarzenia
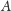 określone jest równością
określone jest równością
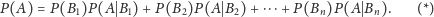 |
Twierdzenie to w skrótowej formie można wypowiedzieć następująco: jeżeli
skutek
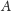 może nastąpić po zaistnieniu jednej z jedynie możliwych,
wykluczających się przyczyn
może nastąpić po zaistnieniu jednej z jedynie możliwych,
wykluczających się przyczyn
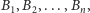 to prawdopodobieństwo
zajścia skutku
to prawdopodobieństwo
zajścia skutku
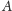 wyraża się wzorem (*).
wyraża się wzorem (*).
Z powyższego twierdzenia wynika kolejne, nazywane twierdzeniem Bayesa.
Twierdzenie (Wzór Bayesa). Jeżeli
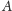 jest zdarzeniem o dodatnim
prawdopodobieństwie, a zdarzenia
jest zdarzeniem o dodatnim
prawdopodobieństwie, a zdarzenia
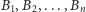 spełniają warunki (a),
(b) i (c) poprzedniego twierdzenia, to prawdopodobieństwo warunkowe
spełniają warunki (a),
(b) i (c) poprzedniego twierdzenia, to prawdopodobieństwo warunkowe
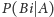 zdarzenia
zdarzenia
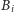 pod warunkiem
pod warunkiem
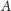 określone jest
równością
określone jest
równością
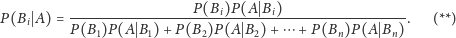 |
Można to wypowiedzieć następująco: jeżeli skutek
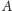 wystąpił po
zaistnieniu jednej z jedynie możliwych, wykluczających się przyczyn
wystąpił po
zaistnieniu jednej z jedynie możliwych, wykluczających się przyczyn
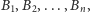 to prawdopodobieństwo tego, że przyczyną zajścia
skutku
to prawdopodobieństwo tego, że przyczyną zajścia
skutku
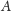 była przyczyna
była przyczyna
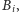 wyraża się wzorem (**).
wyraża się wzorem (**).
Twierdzenie Bayesa określa zatem prawdopodobieństwo przyczyny, gdy wiemy, że nastąpił pewien skutek możliwy do spowodowania przez nią.
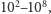 dlatego też przy określaniu
dokładności testu podaje się zazwyczaj logarytm liczby CFU/ml.
dlatego też przy określaniu
dokładności testu podaje się zazwyczaj logarytm liczby CFU/ml.