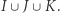Elementarnie o twierdzeniu Brouwera
Tytułowe twierdzenie sformułujemy dla trójkąta (z brzegiem) na płaszczyźnie euklidesowej  Jest to najsłynniejsze i najważniejsze twierdzenie w topologicznej teorii punktów stałych o rozlicznych zastosowaniach (w równaniach różniczkowych, topologii, ekonomii, teorii gier, analizie funkcjonalnej). Jego odkrycie miało ogromny wpływ na rozwój wielu gałęzi matematyki, szczególnie topologii algebraicznej.
Jest to najsłynniejsze i najważniejsze twierdzenie w topologicznej teorii punktów stałych o rozlicznych zastosowaniach (w równaniach różniczkowych, topologii, ekonomii, teorii gier, analizie funkcjonalnej). Jego odkrycie miało ogromny wpływ na rozwój wielu gałęzi matematyki, szczególnie topologii algebraicznej.
Twierdzenie 1 (Luitzen Brouwer, 1912 r.). Niech 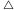 będzie trójkątem i
będzie trójkątem i 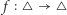 przekształceniem ciągłym. Wtedy istnieje taki punkt
przekształceniem ciągłym. Wtedy istnieje taki punkt 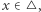 że
że 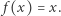
Punktem wyjścia będzie bastępująca kombinatoryczna obserwacja.
Lemat 1 (Emanuel Sperner, 1928 r.). Niech  będzie trójkątem o bokach
będzie trójkątem o bokach  który jest podzielony siecią trójkątów tak, że dwa trójkąty sieci mogą stykać się wspólnym bokiem lub wspólnym wierzchołkiem. Wierzchołki sieci malujemy kolorem czerwonym, niebieskim lub zielonym
który jest podzielony siecią trójkątów tak, że dwa trójkąty sieci mogą stykać się wspólnym bokiem lub wspólnym wierzchołkiem. Wierzchołki sieci malujemy kolorem czerwonym, niebieskim lub zielonym  tak, aby każdy wierzchołek leżący w
tak, aby każdy wierzchołek leżący w 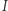 był czerwony lub niebieski, każdy wierzchołek w
był czerwony lub niebieski, każdy wierzchołek w 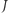 był niebieski lub zielony, a każdy wierzchołek w
był niebieski lub zielony, a każdy wierzchołek w 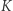 był zielony lub czerwony. Wtedy wśród trójkątów sieci istnieje taki, którego wierzchołki są różnych kolorów.
był zielony lub czerwony. Wtedy wśród trójkątów sieci istnieje taki, którego wierzchołki są różnych kolorów.
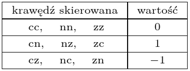
Określmy wartość "oczka" sieci, wędrując w nim przeciwnie do ruchu wskazówek zegara i sumując wartości przyporządkowane krawędziom zgodnie z podaną na marginesie tabelką. Dla trójkąta sieci, którego wierzchołki są różnych kolorów, ta wartość jest równa 3 lub -3. W każdym innym przypadku ta wartość jest równa 0.
Obliczmy sumę wartości wszystkich oczek sieci. Zauważmy, że wkład każdej krawędzi wewnętrznej sieci do całej sumy jest równy 0 (bo krawędź wewnętrzna należy do dwóch trójkątów i wędrujemy po niej w przeciwnych kierunkach), a wkład każdego boku trójkąta  jest równy 1. Zatem suma wartości wszystkich krawędzi sieci trójkąta
jest równy 1. Zatem suma wartości wszystkich krawędzi sieci trójkąta  jest równa 3. Oznacza to, że nie wszystkie oczka sieci mają wartość 0. Istnieje więc w sieci trójkąt, którego wierzchołki są różnych kolorów.
jest równa 3. Oznacza to, że nie wszystkie oczka sieci mają wartość 0. Istnieje więc w sieci trójkąt, którego wierzchołki są różnych kolorów.
Topologiczną konsekwencją lematu Spernera jest następująca obserwacja.
Lemat 2. Niech 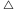 będzie trójkątem o bokach
będzie trójkątem o bokach 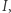
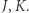 Niech
Niech 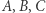 będą zbiorami domkniętymi takimi, że
będą zbiorami domkniętymi takimi, że 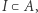
 i
i 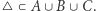 Wtedy
Wtedy 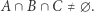
Jeżeli trójkąt 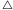 zawiera się w sumie dwóch zbiorów z rodziny
zawiera się w sumie dwóch zbiorów z rodziny  to teza jest spełniona. Załóżmy, że trójkąt
to teza jest spełniona. Załóżmy, że trójkąt 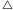 nie zawiera się w sumie dwóch zbiorów z rodziny
nie zawiera się w sumie dwóch zbiorów z rodziny  Dla każdego
Dla każdego 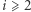 dzielimy boki trójkąta
dzielimy boki trójkąta 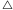 na
na 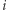 równych części, a łącząc je liniami równoległymi do boków trójkąta, otrzymujemy sieć
równych części, a łącząc je liniami równoległymi do boków trójkąta, otrzymujemy sieć 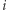 -tego rzędu. Każdy wierzchołek
-tego rzędu. Każdy wierzchołek 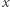 w
w 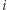 -tej sieci malujemy na dowolny dopuszczalny kolor, który określa przynależność punktu
-tej sieci malujemy na dowolny dopuszczalny kolor, który określa przynależność punktu  do zbiorów z rodziny
do zbiorów z rodziny  Możemy to uczynić w taki sposób, aby wszystkie wierzchołki sieci w
Możemy to uczynić w taki sposób, aby wszystkie wierzchołki sieci w 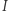 były czerwone lub niebieskie, w
były czerwone lub niebieskie, w 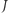 były niebieskie lub zielone, w
były niebieskie lub zielone, w  były zielone lub czerwone. W każdej takiej sieci (lemat 1) istnieje trójkąt o wierzchołkach w różnych kolorach:
były zielone lub czerwone. W każdej takiej sieci (lemat 1) istnieje trójkąt o wierzchołkach w różnych kolorach: 
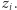 Twierdzenie Bolzano-Weierstrassa zapewnia istnienie podciągu zbieżnego
Twierdzenie Bolzano-Weierstrassa zapewnia istnienie podciągu zbieżnego 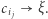 Ponieważ średnice trójkątów kolejnych sieci dążą do 0, więc
Ponieważ średnice trójkątów kolejnych sieci dążą do 0, więc 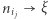 i
i 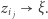 Skoro
Skoro 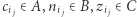 oraz
oraz 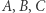 są zbiorami domkniętymi, więc
są zbiorami domkniętymi, więc 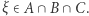
Załóżmy, że 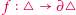 jest takim przekształceniem ciągłym, że
jest takim przekształceniem ciągłym, że 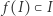 i
i 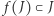 i
i 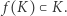 Niech
Niech  Ponieważ
Ponieważ 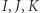 są zbiorami domkniętymi,
są zbiorami domkniętymi,  jest przekształceniem ciągłym, więc zbiory
jest przekształceniem ciągłym, więc zbiory  są domknięte. Oczywiście
są domknięte. Oczywiście 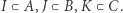 Dla każdego
Dla każdego 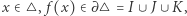 więc
więc 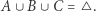 Jednocześnie
Jednocześnie 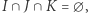 więc
więc  Sprzeczność z lematem 2.
Sprzeczność z lematem 2.
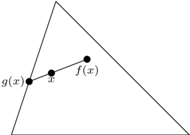
Rys. 1
Załóżmy, że 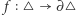 jest takim przekształceniem ciągłym, że
jest takim przekształceniem ciągłym, że 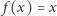 dla
dla 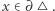 Wtedy
Wtedy 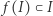 i
i 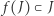 i
i 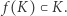 Sprzeczność z lematem 3.
Sprzeczność z lematem 3.
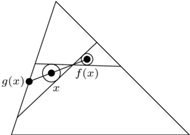
Rys. 2
Dowód twierdzenie. Załóżmy, że 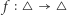 jest przekształceniem ciągłym i
jest przekształceniem ciągłym i 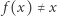 dla każdego
dla każdego 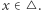 Dla każdego
Dla każdego 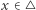 niech
niech 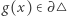 będzie punktem, w którym półprosta wychodząca z punktu
będzie punktem, w którym półprosta wychodząca z punktu 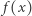 i przechodząca przez punkt
i przechodząca przez punkt  przecina brzeg trójkąta (Rys. 1).
przecina brzeg trójkąta (Rys. 1).
Półprosta jest określona jednoznacznie, bo 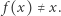 Tak określone przekształcenie
Tak określone przekształcenie 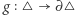 jest ciągłe. Niech
jest ciągłe. Niech  określamy otoczenie punktu
określamy otoczenie punktu 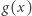 na brzegu
na brzegu  o długości
o długości  Na tym otoczeniu budujemy stożek o wierzchołku na odcinku łączącym punkt
Na tym otoczeniu budujemy stożek o wierzchołku na odcinku łączącym punkt  z
z 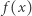 (Rys. 2). Wybieramy
(Rys. 2). Wybieramy 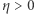 takie, że kula otwarta
takie, że kula otwarta  zawiera się w stożku. Z ciągłości przekształcenia
zawiera się w stożku. Z ciągłości przekształcenia 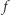 istnieje
istnieje 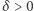 takie, że
takie, że 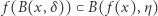 i
i  zawiera się w stożku. Wtedy
zawiera się w stożku. Wtedy 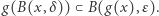 Zatem
Zatem 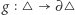 jest przekształceniem ciągłym takim, że
jest przekształceniem ciągłym takim, że  dla
dla 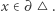 Sprzeczność z lematem 4.
Sprzeczność z lematem 4.
W 1974 roku Mark Yoseloff zauważył, że z twierdzenia Brouwera wynika lemat Spernera (punkt stały przekształcenia 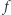 musi należeć do trójkąta sieci, którego wierzchołki są różnych kolorów). Oznacza to, że wszystkie wyżej podane lematy są równoważnikami twierdzenia Brouwera.
musi należeć do trójkąta sieci, którego wierzchołki są różnych kolorów). Oznacza to, że wszystkie wyżej podane lematy są równoważnikami twierdzenia Brouwera.
Twierdzenie Brouwera można wykazać bezpośrednio z lematu 1.

Rys. 3
Drugi dowód twierdzenia. Niech (Rys. 3)
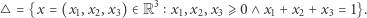 |
Załóżmy, że 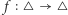 jest przekształceniem ciągłym takim, że
jest przekształceniem ciągłym takim, że 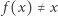 dla każdego
dla każdego  Ponieważ dla nieujemnych wartości
Ponieważ dla nieujemnych wartości 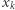 oraz
oraz  i
i 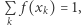 więc z warunku
więc z warunku 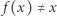 wynika, że przynajmniej jedna ze współrzędnych
wynika, że przynajmniej jedna ze współrzędnych 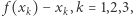 punktu
punktu  musi być ujemna i przynajmniej jedna musi być dodatnia.
musi być ujemna i przynajmniej jedna musi być dodatnia.
Dla każdego 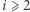 dzielimy boki trójkąta
dzielimy boki trójkąta  na
na  równych części, a łącząc je liniami równoległymi do boków trójkąta, otrzymujemy sieć
równych części, a łącząc je liniami równoległymi do boków trójkąta, otrzymujemy sieć 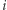 -tego rzędu. Poszczególnym wierzchołkom sieci przypiszemy kolor zielony
-tego rzędu. Poszczególnym wierzchołkom sieci przypiszemy kolor zielony 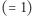 , czerwony
, czerwony 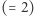 , niebieski
, niebieski  według następującej reguły: kolor wierzchołka
według następującej reguły: kolor wierzchołka  określa najmniejszy indeks
określa najmniejszy indeks  dla którego
dla którego 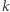 -ta współrzędna punktu
-ta współrzędna punktu 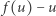 jest ujemna.
jest ujemna.
Oznaczmy boki trójkąta 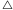 jak na rysunku 3 Jeśli wierzchołek sieci
jak na rysunku 3 Jeśli wierzchołek sieci  leży na boku
leży na boku 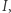 to
to 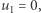 więc pierwsza współrzędna punktu
więc pierwsza współrzędna punktu 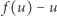 nie może być liczbą ujemną, czyli taki punkt
nie może być liczbą ujemną, czyli taki punkt  nie otrzyma koloru zielonego (1). Analogicznie wierzchołki sieci z boku
nie otrzyma koloru zielonego (1). Analogicznie wierzchołki sieci z boku 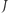 nie otrzymają koloru czerwonego (2), a wierzchołki sieci z boku
nie otrzymają koloru czerwonego (2), a wierzchołki sieci z boku  nie otrzymają koloru niebieskiego (3). W szczególności wierzchołek
nie otrzymają koloru niebieskiego (3). W szczególności wierzchołek 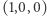 otrzyma kolor zielony, wierzchołek
otrzyma kolor zielony, wierzchołek 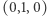 kolor czerwony, wierzchołek
kolor czerwony, wierzchołek 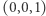 kolor niebieski. Takie kolorowanie wierzchołków sieci jest zgodne z podanym w lemacie 1. Zatem na podstawie lematu 1 w każdej sieci
kolor niebieski. Takie kolorowanie wierzchołków sieci jest zgodne z podanym w lemacie 1. Zatem na podstawie lematu 1 w każdej sieci 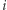 -tego rzędu istnieje trójkąt, którego wierzchołki są różnych kolorów:
-tego rzędu istnieje trójkąt, którego wierzchołki są różnych kolorów:  Na podstawie twierdzenia Bolzano-Weierstrassa istnieje podciąg zbieżny
Na podstawie twierdzenia Bolzano-Weierstrassa istnieje podciąg zbieżny 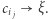 Ponieważ średnice trójkątów kolejnych sieci dążą do 0, więc również
Ponieważ średnice trójkątów kolejnych sieci dążą do 0, więc również 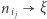 i
i 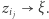 Wówczas z ciągłości przekształcenia
Wówczas z ciągłości przekształcenia  i
i 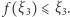 Oznacza to, że żadna ze współrzędnych punktu
Oznacza to, że żadna ze współrzędnych punktu  nie jest liczbą dodatnią, a to jest sprzeczne z warunkiem
nie jest liczbą dodatnią, a to jest sprzeczne z warunkiem 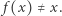
Twierdzenie Brouwera pozostaje prawdziwe w przestrzeniach euklidesowych 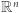 (najczęściej jest ono formułowane dla kul):
(najczęściej jest ono formułowane dla kul):
Twierdzenie. Niech 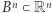 będzie domkniętą kulą i
będzie domkniętą kulą i 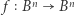 przekształceniem ciągłym. Wtedy istnieje
przekształceniem ciągłym. Wtedy istnieje 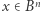 takie, że
takie, że 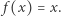
Rezultat ten nie przenosi się do przestrzeni o nieskończonym wymiarze. W przestrzeni 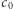 ciągów rzeczywistych zbieżnych do zera z normą
ciągów rzeczywistych zbieżnych do zera z normą 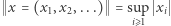 dla kuli domkniętej
dla kuli domkniętej 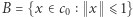 i przekształcenia ciągłego
i przekształcenia ciągłego 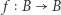 danego wzorem
danego wzorem 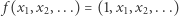 jedynym punktem stałym jest
jedynym punktem stałym jest 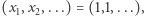 ale
ale 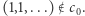
Twierdzenie Brouwera rozszerzył (na nieskończenie wymiarowe przestrzenie Banacha) Juliusz Schauder w 1930 roku, ale to całkiem inna historia...
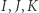
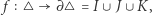
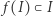
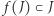
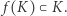
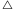
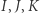
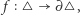

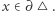
 jest domknięty, jeśli dla dowolnego zbieżnego ciągu elementów
jest domknięty, jeśli dla dowolnego zbieżnego ciągu elementów  granica tego ciągu również należy do
granica tego ciągu również należy do 
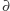 oznacza brzeg, czyli
oznacza brzeg, czyli  oznacza brzeg trójkąta
oznacza brzeg trójkąta 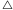 złożony z trzech odcinków
złożony z trzech odcinków