Delta mi!

Tytułowe twierdzenie sformułujemy dla trójkąta (z brzegiem) na płaszczyźnie euklidesowej 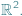Jest to najsłynniejsze i najważniejsze twierdzenie w topologicznej teorii punktów stałych o rozlicznych zastosowaniach (w równaniach różniczkowych, topologii, ekonomii, teorii gier, analizie funkcjonalnej). Jego odkrycie miało ogromny wpływ na rozwój wielu gałęzi matematyki, szczególnie topologii algebraicznej.

Jeśli czytasz ten tekst, to świetnie się składa, możesz poznać drobny fragment topologii i zmierzyć się z następującym pytaniem: Ile topologicznie różnych figur można ułożyć na płaszczyźnie z sześciu zapałek, które stykają się tylko końcami?

W salonie fryzjerskim siedzi matematyk, obok leży połyskująca para nożyczek, mnóstwo szczotek i innych sprzętów. Matematyk nerwowo wierci się w fotelu - przecież nie od dziś wie, że sfery zaczesać się nie da. Fryzjer intuicyjnie sięga po nożyczki, szalejące nad czołem rozmaitości nie rokują zbyt dobrze. Niechętny rozspójnieniu klient wpada na pomysł - warkocz będzie idealny!

Pojęcie spójności przestrzeni metrycznej to uściślenie intuicji, że przestrzeń jest "w jednym kawałku".

Wyobraźmy sobie, że przyszło nam żeglować po jeziorze pod wiatr...

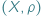Przypuśćmy, że jest przestrzenią metryczną, czyli zbiorem 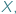w którym możemy mierzyć odległość między punktami tego zbioru. W przestrzeni metrycznej możemy zdefiniować pojęcie zbioru otwartego i domkniętego. Zacznijmy od przykładu podzbiorów płaszczyzny ze zwykłą, szkolną metryką euklidesową.

Homeomorfizmy to przekształcenia zachowujące różne własności zbiorów (obiektów geometrycznych). Znaczy to, że pewne cechy obiektu są zachowywane przy "ściskaniu" lub "rozciąganiu", bez sklejania lub rozcinania, dziurawienia itp.

Jeszcze w r. 1908, pisząc o wspólnym brzegu dwu obszarów płaskich (z których jeden jest ograniczony), Schoenf1ies uważał, że można ten brzeg rozłożyć na dwa luki krzywe (przez luk krzywy rozumiał w tym przypadku kontinuum nie rozcinające płaszczyzny lub, co na jedno tu wychodzi, kontinuum rożne od całego brzegu). Był to błąd, który sprostował Brouwer w pracy Źur Analysis SitlIs"(Mathematische Annalen 68 (1910),422-434)...

Tym razem o własności punktu stałego...

Spójrzmy na poniższe obrazki i nie zastanawiając się, co właściwie przedstawiają, spróbujmy zgadnąć, jak powinien wyglądać kolejny.

Uczciwi złodzieje powinni umieć się dzielić. Oczywiście, dzielić się łupami z innymi uczciwymi złodziejami, którzy pomagali w dokonaniu kradzieży. Można sobie wyobrazić, że taka uczciwość powoduje czasem pewne trudności, gdyż niektóre precjoza mogą być nieskore do podziału. Dla przykładu...

Mapa obok przedstawia rejon Giewontu i Kopy Kondrackiej. Typowa poziomica jest albo pusta (np. nie ma żadnych punktów na wysokości 2500 m), albo składa się z jednej lub więcej składowych, z których każda jest albo zamkniętą pętlą (jak ta wokół Giewontu, 1800 m), albo krzywą o dwóch końcach na brzegu mapy (np. te powyżej dolin Małej Łąki i Kondratowej, 1600 m). Może się jednak zdarzyć, że poziomica jest osobliwa - na wysokości 1894 m mamy izolowany punkt (szczyt Giewontu), a na 1725 m przecięcie w kształcie litery X (Kondracka Przełęcz). Są to jednak pojedyncze przypadki - jak szczyt, przełęcz albo dno kotła - a wszystkie pozostałe poziomice są regularne.

2016 roku Nagroda Nobla z Fizyki została przyznana za teoretyczne odkrycia topologicznych przejść fazowych i topologicznych faz materii. Z kilku przyczyn nagroda ta była dość nietypowa. Komitet Noblowski zdecydował o wyróżnieniu nie pojedynczego, przełomowego odkrycia, ale raczej nagrodził wprowadzenie do fizyki nowych idei, które ukierunkowały i ukształtowały nasz sposób myślenia o fazach materii. Ponadto, co też nietypowe, nagrodzeni badacze to wyłącznie teoretycy, mimo że ich pomysły znalazły późniejsze potwierdzenie eksperymentalne. Komisja zdecydowała też o nierównym podziale nagrody: jej połowę otrzymał David J. Thouless, a drugą połową podzielili się F. Duncan M. Haldane oraz J. Michael Kosterlitz.

Pod koniec lata 2012 roku wśród matematyków rozeszła się wiadomość, że 21 sierpnia zmarł William Thurston, matematyk, laureat medalu Fieldsa. Gdy w październiku 2010 roku zmarł Benoît Mandelbrot, pisały o tym niemal wszystkie gazety, informowały portale społecznościowe. O śmierci Thurstona dowiedzieli się – jak to najczęściej bywa w przypadku matematyków – głównie specjaliści. William Thurston zasłynął z postawienia, pod koniec lat siedemdziesiątych XX stulecia, hipotezy geometryzacyjnej i prób jej udowodnienia. Za te osiągnięcia, a miał jeszcze wiele innych, został uhonorowany medalem Fieldsa na Międzynarodowym Kongresie Matematyków w Warszawie w 1983 roku.

Ideą teorii wymiaru jest przyporządkowanie przestrzeni  liczby całkowitej (wymiaru ) tak, by było to zgodne z intuicyjnym znaczeniem tego słowa. Dla uproszczenia skoncentrujemy się na podzbiorach przestrzeni Hilberta, która zawiera, między innymi, przestrzenie euklidesowe wszystkich wymiarów.

11 listopada 2002 roku Grigorij Jakowlewicz Perelman, geometra pracujący w Petersburskim Oddziale Instytutu Matematycznego im. Stiekłowa przy Fontance 27, udostępnił w Internecie 40-stronicową pracę pod tytułem „Formuła entropii dla potoku Ricciego i jej zastosowania geometryczne”. Czwartą stronę suchego i najeżonego fachowymi terminami wprowadzenia kończy zdanie:
Wreszcie, w rozdziale 13, podajemy krótki szkic dowodu hipotezy geometryzacyjnej.

Powiemy, że dwie bryły są plastelinowo równoważne (w skrócie równoważne), jeśli jedną z nich można otrzymać z drugiej za pomocą rozciągania, ściskania, wyginania itp., ale bez sklejania lub rozrywania.