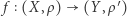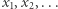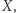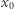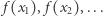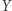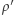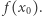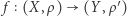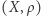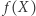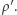Co to jest?
Przestrzeń spójna
Pojęcie spójności przestrzeni metrycznej to uściślenie intuicji, że przestrzeń jest "w jednym kawałku".
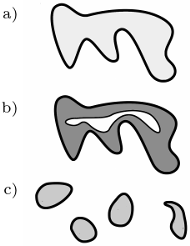
Rysunek c) przedstawia niespójny podzbiór 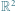 (z metryką euklidesową).
(z metryką euklidesową).
Definicja. Przestrzeń metryczna 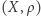 jest spójna, jeżeli nie istnieją niepuste domknięte podzbiory
jest spójna, jeżeli nie istnieją niepuste domknięte podzbiory 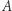 i
i 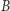 takie, że ich część wspólna jest zbiorem pustym
takie, że ich część wspólna jest zbiorem pustym 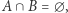 zaś ich suma jest całą przestrzenią
zaś ich suma jest całą przestrzenią 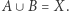
Zbiory 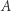 i
i 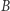 to są właśnie te "kawałki", na które rozpada się przestrzeń
to są właśnie te "kawałki", na które rozpada się przestrzeń 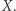 Zauważmy, że gdy przestrzeń nie jest spójna i jest sumą swoich niepustych, domkniętych i rozłącznych podzbiorów, to każdy z tych podzbiorów jest także otwarty.
Zauważmy, że gdy przestrzeń nie jest spójna i jest sumą swoich niepustych, domkniętych i rozłącznych podzbiorów, to każdy z tych podzbiorów jest także otwarty.
Przykład 1. Zbiór liczb wymiernych 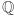 na prostej z metryką
na prostej z metryką 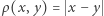 nie jest spójny, bowiem można go przedstawić w postaci sumy
nie jest spójny, bowiem można go przedstawić w postaci sumy
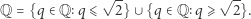
Przykład 2. Podobnie zbiór liczb niewymiernych nie jest spójny, bo można go przedstawić na przykład w postaci
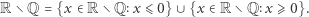
Bardzo ważne przykłady przestrzeni spójnych dostarcza następujące twierdzenie:
Twierdzenie. Następujące przestrzenie metryczne z metryką prostej euklidesowej są spójne dla dowolnych 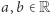 : odcinek otwarty
: odcinek otwarty 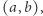 odcinek domknięty
odcinek domknięty ![|[a,b],](/math/temat/matematyka/topologia/2019/03/28/Przestrzen_spojna/3x-75e0c969ea142317c0f834e83b414b0783df3d3a-im-33,33,33-FF,FF,FF.gif) domknięty jednostronnie
domknięty jednostronnie ![|[a, b),(a,b],](/math/temat/matematyka/topologia/2019/03/28/Przestrzen_spojna/4x-75e0c969ea142317c0f834e83b414b0783df3d3a-im-33,33,33-FF,FF,FF.gif) półproste
półproste ![[a,+ ∞ ),(a,+∞ ),(−∞ ,a),(−∞ ,a]](/math/temat/matematyka/topologia/2019/03/28/Przestrzen_spojna/5x-75e0c969ea142317c0f834e83b414b0783df3d3a-im-33,33,33-FF,FF,FF.gif) i cała prosta
i cała prosta 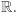 Są to jedyne spójne podzbiory prostej euklidesowej.
Są to jedyne spójne podzbiory prostej euklidesowej.
Jak zachowają się przestrzenie spójne, gdy będziemy je przekształcać? Jeżeli przekształcenie może zgniatać, rozciągać, ale nie rozrywać, to z przestrzeni "w jednym kawałku" otrzymamy również przestrzeń w "jednym kawałku", czyli spójną. Przekształcenia, które nie "rozrywają", nazywamy ciągłymi. "Rozrywanie" to oderwanie punktu granicznego od ciągu punktów do niego zbieżnego. Definicja przekształcenia ciągłego przestrzeni metrycznej znajduje się tutaj.
Rozważmy teraz odcinek ![[0,1]](/math/temat/matematyka/topologia/2019/03/28/Przestrzen_spojna/1x-b6c559d2bb812801e398541aef7a274454822986-im-33,33,33-FF,FF,FF.gif) ze zwykłą metryką. Jeżeli na punkty tego odcinka będziemy patrzeć jak na czas, to na przekształcenie odcinka w przestrzeń
ze zwykłą metryką. Jeżeli na punkty tego odcinka będziemy patrzeć jak na czas, to na przekształcenie odcinka w przestrzeń 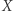 możemy patrzeć jak na szlak przebyty w czasie od 0 do
możemy patrzeć jak na szlak przebyty w czasie od 0 do 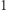 w przestrzeni
w przestrzeni 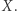 Jeżeli
Jeżeli 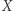 jest przestrzenią metryczną z metryką
jest przestrzenią metryczną z metryką 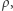 a przekształcenie jest ciągłe, to mówimy, że mamy drogę w przestrzeni metrycznej
a przekształcenie jest ciągłe, to mówimy, że mamy drogę w przestrzeni metrycznej 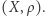 Obraz 0 jest początkiem, a obraz
Obraz 0 jest początkiem, a obraz 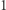 końcem tej drogi. Przestrzenie, w których od jednego do drugiego punktu możemy przejść pewną drogą, są tak ważne, że mają swoją nazwę.
końcem tej drogi. Przestrzenie, w których od jednego do drugiego punktu możemy przejść pewną drogą, są tak ważne, że mają swoją nazwę.
Definicja. Przestrzeń metryczna 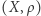 nazywa się łukowo spójna, jeżeli dla dowolnych punktów
nazywa się łukowo spójna, jeżeli dla dowolnych punktów 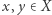 istnieje droga o początku w punkcie
istnieje droga o początku w punkcie  i końcu w punkcie
i końcu w punkcie 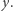
Niech 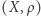 będzie podzbiorem płaszczyzny ze zwykłą metryką euklidesową. Możemy powiedzieć w pewnym uproszczeniu, że podzbiór ten jest łukowo spójny, jeżeli dla każdych dwóch jego punktów można narysować, nie odrywając ołówka od papieru, krzywą łączącą je i zawartą w
będzie podzbiorem płaszczyzny ze zwykłą metryką euklidesową. Możemy powiedzieć w pewnym uproszczeniu, że podzbiór ten jest łukowo spójny, jeżeli dla każdych dwóch jego punktów można narysować, nie odrywając ołówka od papieru, krzywą łączącą je i zawartą w 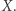


Obraz drogi jest przestrzenią spójną i nietrudno się domyślić, że prawdziwe jest twierdzenie:
Twierdzenie. Jeżeli przestrzeń metryczna 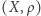 jest łukowo spójna, to jest spójna.
jest łukowo spójna, to jest spójna.
To twierdzenie nietrudno uzasadnić. Jeżeli bowiem 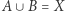 byłoby rozkładem przestrzeni
byłoby rozkładem przestrzeni 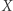 na dwa "kawałki", to weźmy punkt
na dwa "kawałki", to weźmy punkt 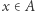 oraz
oraz 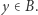 Wiemy, że istnieje droga o początku w punkcie
Wiemy, że istnieje droga o początku w punkcie  i końcu w punkcie
i końcu w punkcie 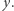 Ale rozkład
Ale rozkład 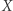 na rozłączne i niepuste domknięte podzbiory
na rozłączne i niepuste domknięte podzbiory 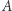 i
i 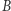 dawałby rozkład obrazu drogi od
dawałby rozkład obrazu drogi od  do
do 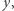 co jest niemożliwe, bo obraz drogi jest przestrzenią spójną.
co jest niemożliwe, bo obraz drogi jest przestrzenią spójną.
Nie każda przestrzeń spójna jest łukowo spójna. Rozważmy przykład podzbioru płaszczyzny, który jest jakby grzebieniem o nieskończenie wielu zębach zbiegających do granicznego zęba. Tego granicznego zęba jednak brakuje - jest tylko jego kawałek (oznaczony na rysunku literą 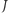 ), nieprzymocowany do grzebienia. Cała przestrzeń jest jednak spójna - ten kawałek nie odpadnie, choć nie ma drogi, która łączy punkt odcinka
), nieprzymocowany do grzebienia. Cała przestrzeń jest jednak spójna - ten kawałek nie odpadnie, choć nie ma drogi, która łączy punkt odcinka 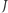 z jakimkolwiek punktem grzebienia, który do odcinka
z jakimkolwiek punktem grzebienia, który do odcinka 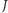 nie należy. To jest jakby spójność "na magnes". Magnes tworzą zbieżne ciągi, które "przyciągają" swoją granicę.
nie należy. To jest jakby spójność "na magnes". Magnes tworzą zbieżne ciągi, które "przyciągają" swoją granicę.
Jeszcze lepiej zjawisko to ilustruje spójna przestrzeń, przypominająca znak polskiego lotnictwa, powstała z nieskończenie wielu patyczków.
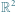 (z metryką euklidesową).
(z metryką euklidesową).