Co to jest?
Zbiór domknięty i zbiór otwarty
Przypuśćmy, że 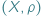 jest przestrzenią metryczną, czyli zbiorem
jest przestrzenią metryczną, czyli zbiorem 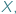 w którym możemy mierzyć odległość między punktami tego zbioru. W przestrzeni metrycznej możemy zdefiniować pojęcie zbioru otwartego i domkniętego. Zacznijmy od przykładu podzbiorów płaszczyzny ze zwykłą, szkolną metryką euklidesową.
w którym możemy mierzyć odległość między punktami tego zbioru. W przestrzeni metrycznej możemy zdefiniować pojęcie zbioru otwartego i domkniętego. Zacznijmy od przykładu podzbiorów płaszczyzny ze zwykłą, szkolną metryką euklidesową.
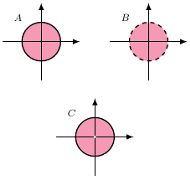
Rozważmy trzy podzbiory:

 różni się od zbiorów
różni się od zbiorów  i
i  tym, że "nic nie brakuje na brzegu". Uściślenie "niczego nie brakuje" jest następujące: jeżeli ciąg punktów
tym, że "nic nie brakuje na brzegu". Uściślenie "niczego nie brakuje" jest następujące: jeżeli ciąg punktów  zbioru
zbioru  jest zbieżny do punktu
jest zbieżny do punktu  płaszczyzny, to punkt
płaszczyzny, to punkt  również należy do zbioru
również należy do zbioru  Zbiory
Zbiory  i
i  nie mają tej własności. W zbiorze
nie mają tej własności. W zbiorze  na przykład ciąg punktów
na przykład ciąg punktów  jest zbieżny do punktu
jest zbieżny do punktu  ale ten do zbioru
ale ten do zbioru  nie należy. W przypadku zbioru
nie należy. W przypadku zbioru  każdy punkt płaszczyzny należący do okręgu
każdy punkt płaszczyzny należący do okręgu  jest granicą pewnego zbieżnego ciągu punktów zbioru
jest granicą pewnego zbieżnego ciągu punktów zbioru  ale do zbioru
ale do zbioru  nie należy. Powiemy, że zbiór
nie należy. Powiemy, że zbiór  jest domknięty, a zbiory
jest domknięty, a zbiory  i
i  domknięte nie są.
domknięte nie są.Definicja. Niech 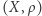 będzie przestrzenią metryczną. Powiemy, że podzbiór
będzie przestrzenią metryczną. Powiemy, że podzbiór 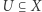 jest domknięty w przestrzeni
jest domknięty w przestrzeni 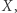 jeżeli dla każdego zbieżnego ciągu punktów zbioru
jeżeli dla każdego zbieżnego ciągu punktów zbioru 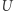 jego granica także należy do
jego granica także należy do 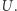
Definicja. Niech 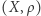 będzie przestrzenią metryczną. Powiemy, że podzbiór
będzie przestrzenią metryczną. Powiemy, że podzbiór 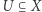 jest otwarty w przestrzeni
jest otwarty w przestrzeni 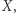 jeżeli zbiór
jeżeli zbiór 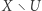 jest domknięty.
jest domknięty.
W powyższym przykładzie zbiór 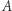 jest domknięty, ale nie jest otwarty, zbiór
jest domknięty, ale nie jest otwarty, zbiór 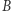 nie jest domknięty, ale jest otwarty, zaś zbiór
nie jest domknięty, ale jest otwarty, zaś zbiór 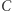 nie jest ani otwarty, ani domknięty na płaszczyźnie euklidesowej.
nie jest ani otwarty, ani domknięty na płaszczyźnie euklidesowej.
W dowolnej przestrzeni metrycznej 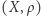 możemy zdefiniować pojęcie kuli o środku w punkcie
możemy zdefiniować pojęcie kuli o środku w punkcie  i promieniu
i promieniu  - jest to po prostu zbiór punktów przestrzeni
- jest to po prostu zbiór punktów przestrzeni 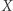 odległych od
odległych od  o ściśle mniej niż
o ściśle mniej niż 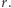 Zauważmy, że podzbiór
Zauważmy, że podzbiór 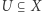 przestrzeni metrycznej
przestrzeni metrycznej 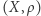 jest otwarty, jeżeli dla każdego punktu
jest otwarty, jeżeli dla każdego punktu 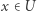 istnieje takie
istnieje takie 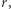 że kula o środku w punkcie
że kula o środku w punkcie 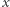 i promieniu
i promieniu  jest zawarta w
jest zawarta w 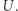
Rozważmy jeszcze następujące dwa przykłady. Niech 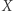 będzie zbiorem punktów płaszczyzny o obu współrzędnych całkowitych. Na zbiorze
będzie zbiorem punktów płaszczyzny o obu współrzędnych całkowitych. Na zbiorze 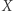 rozważmy metrykę euklidesową. Zauważmy, że w tej przestrzeni metrycznej dowolne dwa punkty są odległe co najmniej o
rozważmy metrykę euklidesową. Zauważmy, że w tej przestrzeni metrycznej dowolne dwa punkty są odległe co najmniej o 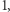 a więc ciągi zbieżne to takie, które są stałe od pewnego miejsca. Wynika z tego, że każdy podzbiór tej przestrzeni metrycznej jest domknięty, zatem każdy podzbiór jest też otwarty. Przestrzeń metryczna o tej własności, że każdy jej podzbiór jest domknięty lub równoważnie każdy jest otwarty, nazywa się dyskretną . W przestrzeni dyskretnej w szczególności każdy jednopunktowy podzbiór jest otwarty - dla każdego punktu możemy więc znaleźć taką kulę, że nie ma w niej punktów innych niż jej środek. Stąd nazwa tej przestrzeni: możemy żartobliwie powiedzieć, że każdy punkt przestrzeni ma zapewnioną dyskrecję - nie ma dowolnie bliskich sąsiadów.
a więc ciągi zbieżne to takie, które są stałe od pewnego miejsca. Wynika z tego, że każdy podzbiór tej przestrzeni metrycznej jest domknięty, zatem każdy podzbiór jest też otwarty. Przestrzeń metryczna o tej własności, że każdy jej podzbiór jest domknięty lub równoważnie każdy jest otwarty, nazywa się dyskretną . W przestrzeni dyskretnej w szczególności każdy jednopunktowy podzbiór jest otwarty - dla każdego punktu możemy więc znaleźć taką kulę, że nie ma w niej punktów innych niż jej środek. Stąd nazwa tej przestrzeni: możemy żartobliwie powiedzieć, że każdy punkt przestrzeni ma zapewnioną dyskrecję - nie ma dowolnie bliskich sąsiadów.
Na koniec zauważmy, że jeżeli 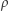 i
i 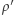 są równoważnymi metrykami na zbiorze
są równoważnymi metrykami na zbiorze 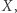 to rodziny domkniętych podzbiorów przestrzeni metrycznej
to rodziny domkniętych podzbiorów przestrzeni metrycznej 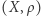 i
i 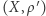 są te same. Ta uwaga sugeruje, że pojęcie domkniętości i otwartości zależy od struktury ogólniejszej od metryki - tak jest w istocie, ale to już jest inna opowieść.
są te same. Ta uwaga sugeruje, że pojęcie domkniętości i otwartości zależy od struktury ogólniejszej od metryki - tak jest w istocie, ale to już jest inna opowieść.
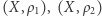 będą przestrzeniami metrycznymi. Metryki
będą przestrzeniami metrycznymi. Metryki 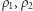 nazywa się równoważnymi, jeżeli granice dowolnych ciągów są identyczne z użyciem obu tych metryk.
nazywa się równoważnymi, jeżeli granice dowolnych ciągów są identyczne z użyciem obu tych metryk.