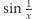Nieuchwytny punkt stały
Tym razem o własności punktu stałego...
Twierdzenie. Jeżeli ![|I = [a,b]](/math/temat/matematyka/topologia/2018/09/28/Nieuchwytny_punkt_staly/1x-24ae1976373229107118af607fa248109ee54701-im-33,33,33-FF,FF,FF.gif) jest domkniętym, ograniczonym przedziałem prostej euklidesowej
jest domkniętym, ograniczonym przedziałem prostej euklidesowej  to każde przekształcenie ciągłe
to każde przekształcenie ciągłe 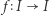 ma punkt stały, tj. taki punkt
ma punkt stały, tj. taki punkt 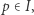 że
że 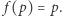
Istotnie, rozważmy funkcję 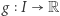 określoną wzorem
określoną wzorem 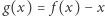 dla każdego
dla każdego 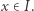 Ponieważ
Ponieważ  i
i 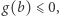 więc z twierdzenia o przyjmowaniu wartości pośrednich istnieje punkt
więc z twierdzenia o przyjmowaniu wartości pośrednich istnieje punkt 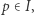 dla którego
dla którego  czyli
czyli 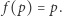
Można też rozumować inaczej: niech 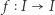 będzie przekształceniem ciągłym,
będzie przekształceniem ciągłym,

Oczywiście, 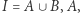
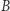 są zbiorami domkniętymi w
są zbiorami domkniętymi w 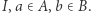 Ponieważ
Ponieważ  jest zbiorem spójnym, więc istnieje punkt
jest zbiorem spójnym, więc istnieje punkt 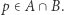 Wtedy
Wtedy 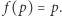
Świetnie, ale gdzie (jak) tego punktu 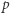 szukać? To jest problem!
szukać? To jest problem!
W 1912 roku Luitzen Brouwer opublikował niezwykle zaskakujący wynik:
Twierdzenie. Na płaszczyźnie euklidesowej 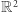 każde przekształcenie ciągłe koła domkniętego
każde przekształcenie ciągłe koła domkniętego 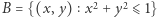 w siebie ma punkt stały.
w siebie ma punkt stały.
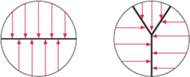
Uzasadnienie tego rezultatu nie jest łatwe, intuicja nam w tym nie pomaga. Weźmy papierową kopię koła 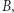 zgniećmy ją dowolnie (ale jej nie rozerwijmy), to, co otrzymaliśmy, zdepczmy tak, by stało się częścią koła
zgniećmy ją dowolnie (ale jej nie rozerwijmy), to, co otrzymaliśmy, zdepczmy tak, by stało się częścią koła 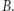 Wtedy co najmniej jeden punkt kopii będzie leżał dokładnie nad swoim pierwowzorem. Zadziwiające!
Wtedy co najmniej jeden punkt kopii będzie leżał dokładnie nad swoim pierwowzorem. Zadziwiające!
I w tym przypadku nie mamy żadnych precyzyjnych informacji o ilości punktów stałych i ich lokalizacji (aproksymacji).

Rys. 1 Zbiory homeomorficzne, dyski topologiczne
Odkryta przez Brouwera własność koła pozostaje prawdziwa dla szerszej klasy zbiorów. Mówimy, że dwa zbiory 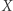 i
i 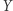 są homeomorficzne, jeśli istnieje takie wzajemnie jednoznaczne przekształcenie
są homeomorficzne, jeśli istnieje takie wzajemnie jednoznaczne przekształcenie 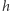 zbioru
zbioru 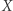 na zbiór
na zbiór 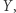 że przekształcenia
że przekształcenia 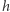 i
i  do niego odwrotne, są ciągłe. Takie przekształcenie
do niego odwrotne, są ciągłe. Takie przekształcenie 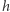 nazywamy homeomorfizmem. Zbiór homeomorficzny z kołem
nazywamy homeomorfizmem. Zbiór homeomorficzny z kołem  nazywamy dyskiem topologicznym (rys. 1).
nazywamy dyskiem topologicznym (rys. 1).
Mówimy, że zbiór 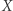 ma własność punktu stałego, gdy każde przekształcenie ciągłe
ma własność punktu stałego, gdy każde przekształcenie ciągłe  ma punkt stały.
ma punkt stały.
Twierdzenie 1. Niech 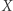 i
i  będą zbiorami homeomorficznymi. Jeżeli zbiór
będą zbiorami homeomorficznymi. Jeżeli zbiór  ma własność punktu stałego, to zbiór
ma własność punktu stałego, to zbiór 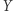 też ma własność punktu stałego.
też ma własność punktu stałego.
Istotnie, niech  będzie przekształceniem ciągłym. Określamy przekształcenie ciągłe
będzie przekształceniem ciągłym. Określamy przekształcenie ciągłe  czyli
czyli 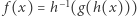 dla każdego
dla każdego 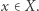 Ponieważ zbiór
Ponieważ zbiór  ma własność punktu stałego, więc istnieje
ma własność punktu stałego, więc istnieje  że
że 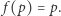 Wtedy
Wtedy 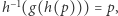 więc
więc 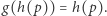 Oznacza to, że
Oznacza to, że 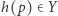 jest punktem stałym przekształcenia
jest punktem stałym przekształcenia 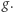 Zbiór
Zbiór 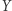 ma więc własność punktu stałego.
ma więc własność punktu stałego.
Twierdzenie Brouwera zapewnia więc, że na płaszczyźnie euklidesowej dysk topologiczny ma własność punktu stałego. Dyski topologiczne należą do szerszej klasy zbiorów, tzw. continuów. Continuum to zbiór zwarty i spójny.

Rys. 2
Nie wszystkie continua (na płaszczyźnie euklidesowej) mają własność punktu stałego. Dla okręgu, czy pierścienia niewielki obrót lub przekształcenie antypodyczne rusza wszystkie punkty figury. Z drugiej strony wiele continuów ma własność punktu stałego.
Oznaczmy łuk 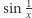 przez
przez 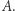 Niech
Niech 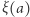 oznacza współrzędną
oznacza współrzędną 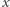 -ową punktu
-ową punktu 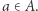 Dla dowolnego przekształcenia ciągłego
Dla dowolnego przekształcenia ciągłego 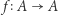 funkcja
funkcja 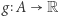 dana wzorem
dana wzorem 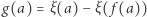 jest ciągła i nieujemna w punkcie
jest ciągła i nieujemna w punkcie  Na odcinku
Na odcinku  funkcja
funkcja 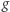 jest niedodatnia. Jeżeli funkcja
jest niedodatnia. Jeżeli funkcja  przyjmuje wartość zero w pewnym punkcie zbioru
przyjmuje wartość zero w pewnym punkcie zbioru 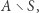 to jest to punkt stały przekształcenia
to jest to punkt stały przekształcenia 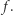 Jeśli
Jeśli 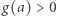 we wszystkich punktach
we wszystkich punktach 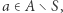 to
to 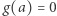 na zbiorze
na zbiorze 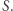 Oznacza to jednak, że
Oznacza to jednak, że 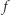 przekształca zbiór
przekształca zbiór 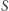 w
w  a takie przekształcenie ma punkt stały w zbiorze
a takie przekształcenie ma punkt stały w zbiorze 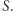
Rys. 3
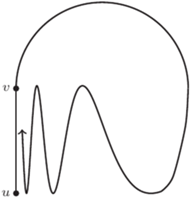
Oznaczmy okrąg 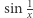 przez
przez 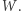 Niech
Niech 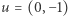 i dla każdego punktu
i dla każdego punktu 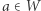 niech
niech 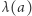 będzie długością łuku, wzdłuż okręgu
będzie długością łuku, wzdłuż okręgu  od punktu
od punktu 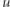 do punktu
do punktu 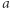 (np.
(np. 
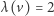 ). Dla dowolnego przekształcenia ciągłego
). Dla dowolnego przekształcenia ciągłego  funkcja
funkcja 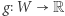 dana wzorem
dana wzorem 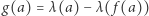 jest ciągła oraz
jest ciągła oraz  Jeśli w zbiorze
Jeśli w zbiorze  jest punkt, dla którego funkcja
jest punkt, dla którego funkcja 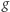 jest nieujemna, to w pewnym punkcie
jest nieujemna, to w pewnym punkcie 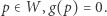 Wtedy
Wtedy 
Warunek 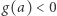 dla każdego punktu
dla każdego punktu 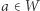 oznacza, że punkt
oznacza, że punkt 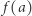 znajduje się na wykresie funkcji
znajduje się na wykresie funkcji 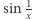 zawsze przed punktem
zawsze przed punktem 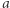 (w tym sensie, że
(w tym sensie, że 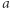 jest punktem łuku łączącego
jest punktem łuku łączącego  i
i 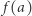 ). Każdy punkt
). Każdy punkt 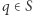 jest granicą ciągu punktów
jest granicą ciągu punktów 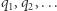 z wykresu funkcji
z wykresu funkcji 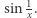 Ponieważ punkt
Ponieważ punkt 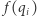 leży przed punktem
leży przed punktem 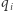 na wykresie funkcji
na wykresie funkcji 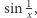 więc z ciągłości przekształcenia
więc z ciągłości przekształcenia 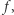
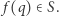 Oznacza to, że
Oznacza to, że 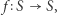 w konsekwencji
w konsekwencji 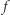 ma punkt stały w zbiorze
ma punkt stały w zbiorze 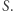
W badaniu własności punktu stałego bardzo użyteczny jest następujący rezultat.
Twierdzenie 2. Niech 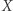 będzie zbiorem z własnością punktu stałego,
będzie zbiorem z własnością punktu stałego,  jego podzbiorem i
jego podzbiorem i  takim przekształceniem ciągłym, że
takim przekształceniem ciągłym, że 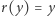 dla każdego
dla każdego 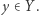 Wtedy zbiór
Wtedy zbiór 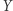 też ma własność punktu stałego.
też ma własność punktu stałego.
Uzasadnienie jest proste. Niech 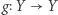 będzie przekształceniem ciągłym. Wtedy przekształcenie
będzie przekształceniem ciągłym. Wtedy przekształcenie 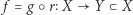 jest ciągłe. Ponieważ zbiór
jest ciągłe. Ponieważ zbiór 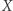 ma własność punktu stałego, więc istnieje takie
ma własność punktu stałego, więc istnieje takie 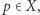 że
że 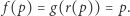 Ponieważ
Ponieważ 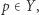 więc z warunku
więc z warunku 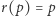 wynika, że
wynika, że 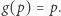
Rys. 4

Rys. 5
Zbiór 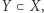 dla którego istnieje takie przekształcenie ciągłe
dla którego istnieje takie przekształcenie ciągłe  że
że 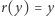 dla każdego
dla każdego 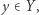 nazywamy retraktem zbioru
nazywamy retraktem zbioru 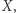 a przekształcenie
a przekształcenie  nazywamy retrakcją. Pojęcia te wprowadził w 1931 roku Karol Borsuk.
nazywamy retrakcją. Pojęcia te wprowadził w 1931 roku Karol Borsuk.
Odcinek i litera 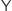 są retraktami koła
są retraktami koła 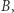 więc mają własność punktu stałego (rys. 4). Continua z rysunku 5 też są retraktami koła
więc mają własność punktu stałego (rys. 4). Continua z rysunku 5 też są retraktami koła 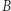 i zgodnie z twierdzeniem 2 mają własność punktu stałego.
i zgodnie z twierdzeniem 2 mają własność punktu stałego.

Rys. 6
Oczywiście, aby wykazać, że zbiór nie ma własności punktu stałego, wystarczy wskazać przykład jednego przekształcenia ciągłego, które rusza wszystkie punkty zbioru (lub jego retraktu). Sprawdź, które litery alfabetu łacińskiego mają własność punktu stałego (a innych alfabetów?). Dla przykładu rozpatrzmy pierwsze dwie litery (rys. 6), jak widać, obie nie mają własności punktu stałego.
Drogi Czytelniku, w poniższych zadaniach, zanim przeczytasz rozwiązania, sam zmierz się z pytaniami.
Zadanie 1. Czy "bałwanek", gdzie koła domknięte 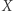 i
i 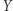 są styczne zewnętrznie, ma własność punktu stałego?
są styczne zewnętrznie, ma własność punktu stałego?
Rozwiązanie: Wystarczy zauważyć, że "bałwanek" jest retraktem koła, które zgodnie z twierdzeniem Brouwera ma własność punktu stałego. Wniosek: "bałwanek" 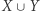 ma własność punktu stałego.
ma własność punktu stałego.
A jak wygląda sytuacja, gdy zbiory 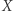 i
i  są dyskami topologicznymi i mają więcej punktów wspólnych?
są dyskami topologicznymi i mają więcej punktów wspólnych?
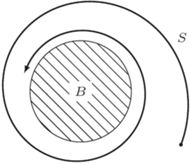
Rys. 7
Zadanie 2. Czy koło domknięte 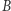 z nawijającą się asymptotycznie na jego brzeg spiralą
z nawijającą się asymptotycznie na jego brzeg spiralą  (rys. 7) ma własność punktu stałego?
(rys. 7) ma własność punktu stałego?
Rozwiązanie: Jeżeli  jest przekształceniem ciągłym, to albo
jest przekształceniem ciągłym, to albo 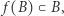 albo
albo  (zbiór
(zbiór  nie jest łukowo spójny, a jedynie jest sumą zbiorów łukowo spójnych). Analogicznie,
nie jest łukowo spójny, a jedynie jest sumą zbiorów łukowo spójnych). Analogicznie, 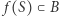 albo
albo 
Jeżeli 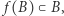 to na podstawie twierdzenia Brouwera
to na podstawie twierdzenia Brouwera 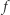 ma punkt stały.
ma punkt stały.
Jeżeli 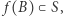 to również
to również 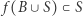 (
( 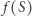 nie może wtedy zawierać się w zbiorze
nie może wtedy zawierać się w zbiorze 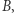 bo
bo 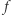 jest ciągłe). Ponieważ zbiór
jest ciągłe). Ponieważ zbiór 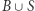 jest zwarty, więc zbiór
jest zwarty, więc zbiór 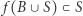 jest punktem albo domkniętym łukiem skończonej długości
jest punktem albo domkniętym łukiem skończonej długości 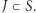 Jeżeli
Jeżeli 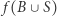 jest punktem, to jest to punkt stały przekształcenia
jest punktem, to jest to punkt stały przekształcenia 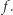 W przeciwnym przypadku
W przeciwnym przypadku 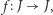 a to przekształcenie ma punkt stały. Zatem continuum
a to przekształcenie ma punkt stały. Zatem continuum 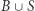 ma własność punktu stałego.
ma własność punktu stałego.
Opisane zagadnienia prowadzą do wielu otwartych pytań. Jedno z najważniejszych, postawione około 1930 r., jest następujące:
Problem. Czy każde continuum, które nie rozcina płaszczyzny, ma własność punktu stałego?
Niestety, nie znamy na nie odpowiedzi. Jednym z powodów takiego stanu rzeczy jest niezwykle bogaty i różnorodny ogród anomalii jaki stanowią continua. Przykładem niech będzie pytanie: czy na płaszczyźnie istnieją linie będące wspólnym brzegiem trzech (lub więcej) obszarów? Odpowiedź podał Brouwer w 1910 roku, budując na płaszczyźnie dla każdego naturalnego  wspólne brzegi
wspólne brzegi  obszarów. Spróbuj i Ty!
obszarów. Spróbuj i Ty!
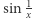
![sin 1x,x∈ (0,1],](/math/temat/matematyka/topologia/2018/09/28/Nieuchwytny_punkt_staly/2x-580c2707db7f1b221d0777093280caf37c31261c-im-33,33,33-FF,FF,FF.gif)