Topologia na Antypodach
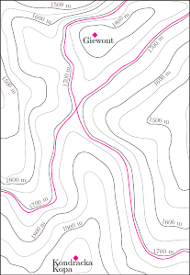
Typowe (regularne) poziomice zaznaczone są na szaro, a nietypowe (osobliwe) na kolorowo.
Mapa obok przedstawia rejon Giewontu i Kopy Kondrackiej. Typowa poziomica jest albo pusta (np. nie ma żadnych punktów na wysokości 2500 m), albo składa się z jednej lub więcej składowych, z których każda jest albo zamkniętą pętlą (jak ta wokół Giewontu, 1800 m), albo krzywą o dwóch końcach na brzegu mapy (np. te powyżej dolin Małej Łąki i Kondratowej, 1600 m). Może się jednak zdarzyć, że poziomica jest osobliwa - na wysokości 1894 m mamy izolowany punkt (szczyt Giewontu), a na 1725 m przecięcie w kształcie litery X (Kondracka Przełęcz). Są to jednak pojedyncze przypadki - jak szczyt, przełęcz albo dno kotła - a wszystkie pozostałe poziomice są regularne.
W matematyce pojęcie poziomicy pojawia się w podobnym, nieco ogólniejszym kontekście. Poziomicą funkcji 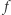 wyznaczoną przez wartość
wyznaczoną przez wartość 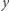 nazywamy zbiór tych wszystkich argumentów
nazywamy zbiór tych wszystkich argumentów 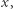 dla których
dla których 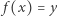 ; zbiór ten oznaczamy przez
; zbiór ten oznaczamy przez 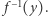 W poprzednim akapicie rozważaliśmy funkcję
W poprzednim akapicie rozważaliśmy funkcję 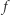 przyporządkowującą punktowi
przyporządkowującą punktowi 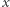 na mapie jego wysokość, ale to tylko jedna z możliwości. W ogólnym przypadku można wykazać (mówi o tym tzw. twierdzenie Sarda), że prawie każda poziomica gładkiej funkcji
na mapie jego wysokość, ale to tylko jedna z możliwości. W ogólnym przypadku można wykazać (mówi o tym tzw. twierdzenie Sarda), że prawie każda poziomica gładkiej funkcji 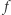 jest regularna, a więc - podobnie jak w przypadku kartograficznym - osobliwe poziomice są zjawiskiem nietypowym.
jest regularna, a więc - podobnie jak w przypadku kartograficznym - osobliwe poziomice są zjawiskiem nietypowym.
W ramach dalszego śledzenia poziomic pokażemy teraz, że na równiku Ziemi można znaleźć dwa punkty antypodyczne leżące na jednej poziomicy. Punkty antypodyczne to takie, że tunel wydrążony z jednego z nich na wylot przez środek Ziemi wypada w drugim; z dobrym przybliżeniem tak położone są Quito w Ekwadorze (2850 m n.p.m.) i Pekanbaru w Indonezji (12 m n.p.m.). Jeśli w każdym z tych dwóch miast mamy znajomego, możemy ich poprosić o udanie się w podróż na zachód w tym samym tempie i informowanie na bieżąco o aktualnej wysokości nad poziomem morza. O ile na początku znajomy z Ekwadoru jest ponad 2 km wyżej, to sytuacja będzie się szybko zmieniać, a po pewnym czasie nasi znajomi zamienią się miejscami i różnica w raportowanych wysokościach będzie taka sama, ale na minusie. Niewątpliwie gdzieś po drodze wysokości musiały się wyrównać - w ten sposób znaleźliśmy punkty antypodyczne na jednej poziomicy.
Powyższy przykład jest mało zaskakujący, bo bez niczyjej pomocy z łatwością znajdziemy żądaną parę punktów na pełnym morzu (wysokość 0 m n.p.m.). Przedstawione rozumowanie jest jednak bardziej uniwersalne i działa równie dobrze, gdyby zamienić wysokość na jakąś inną funkcję (średnia roczna temperatura, ciśnienie, suma opadów etc.), byle tylko była ciągła, bo musimy wykluczyć skoki. Możemy też pójść krok dalej i chcieć porównać dwa parametry naraz. Pokażemy więc, że na powierzchni Ziemi można znaleźć dwa punkty antypodyczne o równej średniej rocznej temperaturze i ciśnieniu. Wyniknie to z następującego ogólnego twierdzenia.
Twierdzenie 1 (Karol Borsuk, Stanisław Ulam). Niech

będzie sferą jednostkową, a  dowolną funkcją ciągłą. Wówczas istnieje punkt
dowolną funkcją ciągłą. Wówczas istnieje punkt 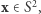 dla którego
dla którego 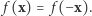
Aby zastosować powyższe twierdzenie do naszej sytuacji, powierzchnię Ziemi modelujemy za pomocą sfery, a odpowiednią funkcję 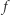 definiujemy poprzez przyporządkowanie punktowi
definiujemy poprzez przyporządkowanie punktowi  pary liczb wyrażających średnią roczną temperaturę i ciśnienie w
pary liczb wyrażających średnią roczną temperaturę i ciśnienie w 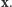 Z twierdzenia otrzymujemy wtedy dwa punkty
Z twierdzenia otrzymujemy wtedy dwa punkty 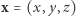 i
i 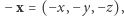 w których oba te parametry mają tę samą wartość. Pozostaje zauważyć, że odpowiada to dokładnie parze punktów antypodycznych na powierzchni Ziemi.
w których oba te parametry mają tę samą wartość. Pozostaje zauważyć, że odpowiada to dokładnie parze punktów antypodycznych na powierzchni Ziemi.
Dla wygody twierdzenie Borsuka-Ulama pokażemy w następującej wersji:
Twierdzenie 2. Załóżmy, że funkcja ciągła 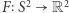 jest nieparzysta, to znaczy spełnia
jest nieparzysta, to znaczy spełnia 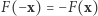 dla każdego
dla każdego 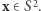 Wówczas
Wówczas 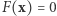 dla pewnego
dla pewnego 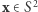 (0 oznacza punkt
(0 oznacza punkt 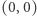 ).
).
Przykładem takiej funkcji jest  czyli rzut prostopadły na płaszczyznę
czyli rzut prostopadły na płaszczyznę 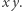 W tym konkretnym przypadku zauważamy, że równość
W tym konkretnym przypadku zauważamy, że równość  zachodzi dla dokładnie dwóch punktów, które na cześć biegunów Ziemi oznaczymy
zachodzi dla dokładnie dwóch punktów, które na cześć biegunów Ziemi oznaczymy 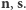 Inny przykład otrzymamy, jeśli weźmiemy dowolny obrót
Inny przykład otrzymamy, jeśli weźmiemy dowolny obrót 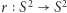 przekształcający sferę na nią samą i określimy funkcję
przekształcający sferę na nią samą i określimy funkcję  ; wówczas miejsca zerowe to
; wówczas miejsca zerowe to 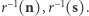 Ale przejdźmy już do ogólnego przypadku.
Ale przejdźmy już do ogólnego przypadku.
Zarys dowodu Twierdzenia 2. Ograniczymy się do wykazania tezy twierdzenia w przypadku, gdy 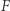 jest funkcją nie tylko ciągłą, ale też gładką. Przypuśćmy, że teza nie zachodzi, czyli
jest funkcją nie tylko ciągłą, ale też gładką. Przypuśćmy, że teza nie zachodzi, czyli  nie przyjmuje zera; będziemy dążyć do sprzeczności.
nie przyjmuje zera; będziemy dążyć do sprzeczności.
Między 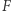 a funkcją
a funkcją 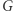 z przykładu wyżej można znaleźć całą rodzinę funkcji
z przykładu wyżej można znaleźć całą rodzinę funkcji
![2 H(x,t) = tF(x) + (1− t)G(x) dla x ∈S ,t ∈[0,1].](/math/temat/matematyka/topologia/2018/08/22/Topologia_na_Antypodach/3x-97dbd598dde187c6dd505967105a1598321e9f14-dm-33,33,33-FF,FF,FF.gif) |
(*) |
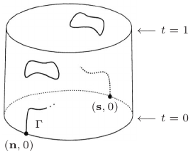
Tak może wyglądać poziomica 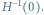 Na potrzeby rysunku denka cylindra są okręgami, a nie sferami.
Na potrzeby rysunku denka cylindra są okręgami, a nie sferami.
Wstawienie 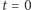 w powyższym wzorze daje na powrót
w powyższym wzorze daje na powrót 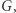 natomiast dla
natomiast dla  otrzymujemy
otrzymujemy 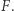 Rodzinę tę możemy też rozumieć jako jedną gładką funkcję
Rodzinę tę możemy też rozumieć jako jedną gładką funkcję ![|H S2 ×[0,1] R2](/math/temat/matematyka/topologia/2018/08/22/Topologia_na_Antypodach/5x-7ddb484b6f7ff10b641bad37996ddf770382c5a0-im-33,33,33-FF,FF,FF.gif) określoną na (pustym w środku) cylindrze
określoną na (pustym w środku) cylindrze ![|S2× [0,1],](/math/temat/matematyka/topologia/2018/08/22/Topologia_na_Antypodach/6x-7ddb484b6f7ff10b641bad37996ddf770382c5a0-im-33,33,33-FF,FF,FF.gif) pokrywającą się z
pokrywającą się z 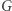 i
i 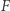 odpowiednio na dolnym
odpowiednio na dolnym 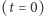 i górnym
i górnym 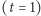 denku.
denku.
Założymy dodatkowo, że poziomica 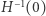 jest regularna. Wówczas składa się ona ze skończenie wielu krzywych, zamkniętych lub mających końce na którymś z denek. Skoro
jest regularna. Wówczas składa się ona ze skończenie wielu krzywych, zamkniętych lub mających końce na którymś z denek. Skoro  nie przyjmuje zera, to
nie przyjmuje zera, to 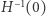 nie może dotykać górnego denka. Wiemy natomiast, że ma dokładnie dwa punkty wspólne z dolnym denkiem (
nie może dotykać górnego denka. Wiemy natomiast, że ma dokładnie dwa punkty wspólne z dolnym denkiem ( 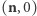 oraz
oraz 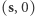 ), gdyż na tym denku
), gdyż na tym denku 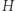 pokrywa się z
pokrywa się z 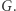 Jak mówi przysłowie, każdy kij ma dwa końce, a więc w skład poziomicy
Jak mówi przysłowie, każdy kij ma dwa końce, a więc w skład poziomicy 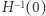 może wchodzić jedynie jedna niezamknięta krzywa
może wchodzić jedynie jedna niezamknięta krzywa ![|Γ ⊆S2 × [0,1],](/math/temat/matematyka/topologia/2018/08/22/Topologia_na_Antypodach/9x-8c3d5dad32e798f116e287f2828ed436a652083b-im-33,33,33-FF,FF,FF.gif) o końcach w
o końcach w  i
i 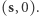
Przypomnijmy teraz, że funkcje 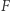 i
i 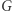 są nieparzyste, a więc zgodnie ze wzorem (*) nieparzysta jest także każda z rodziny funkcji je łączących, to znaczy
są nieparzyste, a więc zgodnie ze wzorem (*) nieparzysta jest także każda z rodziny funkcji je łączących, to znaczy 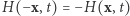 dla dowolnych
dla dowolnych  W konsekwencji poziomica
W konsekwencji poziomica 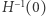 ma następującą własność symetrii: jeśli jakiś punkt
ma następującą własność symetrii: jeśli jakiś punkt 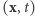 do niej należy, to punkt
do niej należy, to punkt 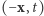 również. Tę samą własność ma więc też krzywa
również. Tę samą własność ma więc też krzywa 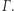 Opisaną sytuację trudno jest jednak wiernie oddać na rysunku, z bardzo prostego powodu - jest niemożliwa!
Opisaną sytuację trudno jest jednak wiernie oddać na rysunku, z bardzo prostego powodu - jest niemożliwa!

Żeby się o tym przekonać, ponownie poprośmy o pomoc naszych sprawdzonych znajomych. Niech obaj podróżują w tym samym tempie wzdłuż krzywej 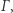 przy czym jeden niech zacznie z punktu
przy czym jeden niech zacznie z punktu  a drugi z
a drugi z 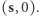 Ze względu na symetrię
Ze względu na symetrię 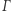 w każdym momencie nasi znajomi będą w punktach postaci
w każdym momencie nasi znajomi będą w punktach postaci 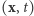 i
i 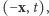 co oznacza, że nie mogą się spotkać. Z drugiej strony, po pewnym czasie każdy z nich dojdzie do przeciwnego końca
co oznacza, że nie mogą się spotkać. Z drugiej strony, po pewnym czasie każdy z nich dojdzie do przeciwnego końca 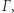 więc po drodze gdzieś musieli się minąć. Otrzymana sprzeczność dowodzi, że funkcja
więc po drodze gdzieś musieli się minąć. Otrzymana sprzeczność dowodzi, że funkcja 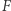 musi przyjmować zero.
musi przyjmować zero.
Wróćmy na chwilę do przyjętego ad hoc założenia o regularności 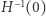 - jest ono spełnione w typowym przypadku, ale nie zawsze. Czytelnik znający twierdzenie Sarda łatwo uzupełni tę lukę, zamieniając w dowodzie funkcję
- jest ono spełnione w typowym przypadku, ale nie zawsze. Czytelnik znający twierdzenie Sarda łatwo uzupełni tę lukę, zamieniając w dowodzie funkcję 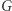 na
na 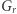 i odpowiednio
i odpowiednio 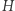 na
na 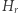 zgodnie ze wzorem (*); można bowiem sprawdzić, że dla prawie każdego obrotu
zgodnie ze wzorem (*); można bowiem sprawdzić, że dla prawie każdego obrotu  poziomica
poziomica  jest regularna, co pozwala przeprowadzić resztę rozumowania bez zmian. Przyjęte na początku założenie o gładkości
jest regularna, co pozwala przeprowadzić resztę rozumowania bez zmian. Przyjęte na początku założenie o gładkości 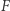 też nietrudno wyrugować.
też nietrudno wyrugować.
Czytelnik obdarzony Szczególnie Czujnym Okiem może zauważyć, że przedstawione rozumowanie równie dobrze stosuje się do funkcji ciągłych  z
z  -wymiarowej sfery w
-wymiarowej sfery w  -wymiarową przestrzeń dla dowolnego
-wymiarową przestrzeń dla dowolnego 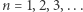 W szczególności dla
W szczególności dla 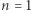 otrzymujemy następujące twierdzenie: dla każdej ciągłej funkcji
otrzymujemy następujące twierdzenie: dla każdej ciągłej funkcji 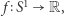 określonej na okręgu, znajdziemy punkt
określonej na okręgu, znajdziemy punkt  w którym
w którym 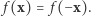 Zatoczyliśmy w ten sposób pełne koło i rozwiązaliśmy w inny sposób początkowy problem z punktami antypodycznymi na równiku.
Zatoczyliśmy w ten sposób pełne koło i rozwiązaliśmy w inny sposób początkowy problem z punktami antypodycznymi na równiku.
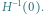 Na potrzeby rysunku denka cylindra są okręgami, a nie sferami.
Na potrzeby rysunku denka cylindra są okręgami, a nie sferami.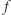 jest gładki, w szczególności nie ma uskoków ani kantów.
jest gładki, w szczególności nie ma uskoków ani kantów.