Okręgi Boromeuszy, czyli matematyk rozplątuje supełki

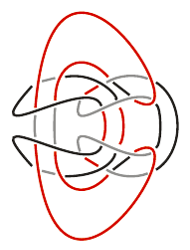
Widoczny obok splot trzech rurek to logo włoskiego rodu Boromeuszy. Splot ten ma interesującą własność: rozcięcie i usunięcie dowolnej z tych rurek sprawia, że pozostałe dwie nie są ze sobą w żaden sposób połączone. W tym miejscu pojawia się naturalne pytanie - czy da się skonstruować splot o podobnej własności dla więcej niż trzech rurek?

Okazuje się, że jest to możliwe - konstrukcja taka (podana przez Martina Gardnera) przedstawiona jest na rysunku dla ośmiu rurek. Oczywiście, w podobny sposób można połączyć także większą liczbę okręgów - dziewięć, dziesięć, jedenaście...
Domyślamy się, że podążając w przeciwnym kierunku, również uzyskamy pożądany rezultat: metodą podaną przez Gardnera można połączyć ze sobą siedem, sześć, ale również pięć, cztery albo trzy okręgi. I w tym miejscu docieramy do kluczowego dla nas pytania - czy splot wykonany w ten sposób z trzech rurek jest równoważny oryginalnemu splotowi Boromeuszy? Innymi słowy - czy jest możliwe przekształcenie jednego z tych splotów w skończonej liczbie ciągłych ruchów w drugi splot?
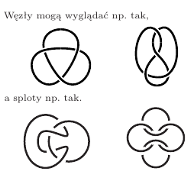
Sprecyzujmy ten problem (a zatem przenieśmy do matematyki). Nie będziemy mówili o rurkach, tylko o węzłach: węzeł to krzywa zamknięta, przykładem jest okrąg (dwa inne przykłady widoczne są obok). Kilka węzłów tworzy splot. Zarówno węzły, jak i sploty rozpatrujemy w przestrzeni trójwymiarowej. Dwa węzły (czy sploty) są równoważne, jeśli przez przemieszczanie i deformowanie (wyginanie, rozciąganie, ale bez rozrywania czy sklejania) można z jednego z nich uzyskać drugi.
Uważny Czytelnik spostrzeże, że to, co widzi obok, to nie są ani węzły, ani sploty - rysunek jest płaski. Taki rysunek to diagram węzła (czy splotu). Wyraźnie zaznaczone są na nim mosty (gdy łuk rysowanej przestrzennej krzywej biegnie nad innym łukiem) i tunele (gdy biegnie pod) - łatwo zauważyć, że liczba mostów i tuneli jest na diagramie taka sama.
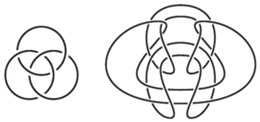
Nasz problem to zbadanie, czy widoczne obok diagramy splotów przedstawiają sploty równoważne, czy jeden z nich można w sposób ciągły przekształcić na drugi. Pytanie takie zostało zadane w Delcie 3/2017, a przedtem i potem powtarza je Matematyczny Cyrk Delty na swoich przedstawieniach.
Odpowiedź jest negatywna - te sploty nie są równoważne. Do wykazania, że tak jest, potrzebne nam będą dwa narzędzia: ruchy podstawowe Reidemeistera i trójkolorowalność węzła (splotu).
Ruchy podstawowe
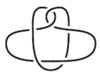
Zacznijmy od oczywistej uwagi, że równoważne węzły czy sploty mogą mieć różne diagramy, np. obok widzimy diagram węzła równoważnego okręgowi. Nawet ten sam węzeł może mieć różne diagramy, bo to jakby jego rzut na dowolnie obraną płaszczyznę.
Niemiecki matematyk, Kurt Reidemeister, w 1927 roku wskazał tzw. ruchy podstawowe i udowodnił, że wszystkie możliwe zmiany diagramu sprowadzają się do tych trzech gatunków ruchów:
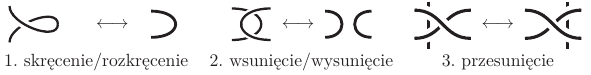
Każde ciągłe przekształcenie węzła (jak później wykazano - również splotu) da się przedstawić na jego diagramie jako ciąg ruchów podstawowych. Badane przez nas sploty są równoważne, jeśli można wskazać przekształcenie jednego z nich w drugi za pomocą wymienionych ruchów podstawowych.
Trójkolorowalność diagramu
Jak łatwo zauważyć, diagram to kilka (kilkanaście, kilkadziesiąt) linii ciągłych, spotykających się w skrzyżowaniach (czyli mostach/tunelach). W każdym skrzyżowaniu spotykają się w diagramie zawsze trzy linie. Pokolorujmy składające się na diagram linie kilkoma kolorami (kolory muszą być co najmniej dwa - diagramy jednokolorowe odrzucamy). Jeśli w każdym skrzyżowaniu spotykają się wszystkie linie w jednym kolorze albo w trzech kolorach, to diagram nazywamy trójkolorowalnym.
Okazuje się, że
jeśli jeden z diagramów węzła (czy splotu) jest trójkolorowalny, to trójkolorowalny jest każdy diagram równoważnego z nim węzła (czy splotu).
Jeśli zatem diagram jakiegoś splotu jest trójkolorowalny, a innego nie, to sploty te nie są równoważne. Innymi słowy - trójkolorowalność (opisana jak wyżej) jest niezmiennikiem topologicznym ruchów podstawowych. Ale uwaga! - podane tu kryterium jest wyłącznie negatywne: jeśli diagramy dwóch splotów są oba trójkolorowalne, to nie wynika z tego, że sploty są równoważne; podobnie, gdy oba nie są trójkolorowalne.
W myśl powyższych uwag wystarczy dowieść, że ruchy Reidemeistera nie psują trójkolorowalności. Będziemy więc rozpatrywali wszystkie możliwe sytuacje, w których można zastosować te ruchy, pamiętając, że po ich wykonaniu końce rozpatrywanego fragmentu muszą pozostać w tym samym kolorze, w jakim były przed.

Jeśli diagram jest pokolorowany zgodnie z wymaganiami trójkolorowalności, to sytuacja, w której możemy zastosować ruch 1, ma miejsce tylko, gdy ten fragment jest pokolorowany jednym kolorem (co widać na marginesie).
Sytuacja, gdy możemy zastosować ruch 2, dopuszcza poniższe dwie możliwości.

Czytelnik skrupulatny sprawdzi, że sytuacja, w której można zastosować ruch 3, dopuszcza pięć pokolorowań.
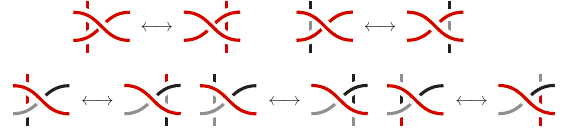
Jak widać, w każdej z sytuacji trójkolorowość jest przez ruchy podstawowe zachowywana.
I to pozwala na wykazanie, że splot trzech okręgów wedle recepty Gardnera jest różny od oryginalnego splotu Boromeuszy - pierwszy z nich jest trójkolorowalny (jak widać na marginesie), a drugi nie, co wykażemy. Spróbujemy bowiem pokolorować go zgodnie z zasadami trójkolorowalności.
Zacznijmy od skrzyżowania 1, kolorując je trzema kolorami. Wówczas na skrzyżowaniu 2 powinniśmy użyć koloru czarnego, ponieważ spotykają się tam już pozostałe. Ten wybór implikowałby pokolorowanie ostatnich dwóch części niepomalowanego okręgu również na czarno, bowiem na skrzyżowaniach 3 i 4 już dwie linie będą czarne (więc i trzecia taka być musi). Ale wtedy skrzyżowania numer 5 i 6 nie spełniałyby ustalonych reguł kolorowania.

Z kolei przyjęcie dla skrzyżowania 1 strategii kolorowania jednym kolorem prowadzi do wniosku, że na skrzyżowaniu 2 również powinniśmy użyć tego koloru. Ale wówczas dla pozostałych niepomalowanych części okręgu należałoby wybrać ten sam kolor, a przecież diagramy jednobarwne wykluczamy.
Stąd wniosek, że splot okręgów Boromeuszy nie jest trójkolorowalny. A zatem nie może być w skończonej liczbie ruchów podstawowych przekształcony na splot gardnerowski - quod erat demonstrandum.

Na sam koniec warto, być może, oddać się następującej refleksji. Na ile w zajmowaniu się matematyką istotna jest intuicja, a na ile formalizm? W przypadku rozwiązania omawianego problemu ważne było jedno i drugie. Tytułowych "supełków" nie dałoby się rozplątać bez wyrobienia w sobie przekonania na temat tego, czy omawiane sploty są równoważne czy też nie - pierwszym etapem znalezienia odpowiedzi była zatem czysta zabawa wyobraźnią. Gdyby na tym jednak poprzestać, całość prac okazałaby się jałowa - formalizm na pewnym etapie był konieczny, by doprowadzić rozumowanie do końca i dojść do rozwiązania.
Oczywiście formalizm, z którego tu korzystaliśmy, był minimalny. Łatwo się jednak domyślić, że w przypadku problemów o większym stopniu złożoności wykorzystuje się bardziej zaawansowany aparat teoretyczny. Parafrazując zatem powszechnie znaną frazę, można by rzec - wyobraźnia jest równie ważna jak wiedza.