Prywatność w morzu danych
Jak dobrze wiemy, żyjemy w wyjątkowym okresie w dziejach, w którym dostęp do informacji jest niesłychanie łatwy, i w zasadzie z roku na rok ułatwienia w tym zakresie zwiększają się. Z pewnością tym bardziej zwiększą się one w bieżącym roku - 2020. Podobnie jest z ilością danych, zbieramy ich coraz więcej. Gromadzimy olbrzymie ilości zdjęć, muzyki, filmów, ale również i innych danych, takich jak teksty, wszelkiego rodzaju informacje o ruchu w sieci itd. Przykładowo w ciągu każdej minuty na serwis YouTube wrzucanych jest około 500 godzin filmów. Powstała nawet dziedzina badań zajmująca się analizą dużych danych, zwana z angielska Big Data...
To właśnie zwiększająca się dostępność do dużych danych oraz zwiększająca się moc obliczeniowa procesorów pozwoliły na fantastyczny rozwój sztucznej inteligencji w ostatnich latach. Dzięki danym jesteśmy świadkami rewolucji w podejściu do wielu problemów. Na przykład dawniej próbowano dokonywać automatycznego tłumaczenia tekstów, bazując na gramatycznej dekompozycji zdań. Teraz Google Translate robi to zupełnie inaczej. Korzysta z dużej bazy tekstów, które są już przetłumaczone na różne języki. Dysponując wieloma tekstami, które zna zarówno w polskiej, jak i angielskiej wersji, używa metod sztucznej inteligencji, żeby określić, które frazy odpowiadają którym frazom w drugim języku.
Dostępność dużych danych w połączeniu z metodami ich analizy, m.in. statystyką oraz sztuczną inteligencją, mogą bardzo przydać się ludzkości. Nietrudno sobie wyobrazić, że można w ten sposób uzyskać choćby postępy w medycynie, na przykład usprawniając metody analizy obrazów, lub zrozumieć lepiej sposób, w jaki my ludzie funkcjonujemy w świecie i komunikujemy się między sobą. Problem w tym, że takie dane dotyczą konkretnych osób i czasem są to dane wrażliwe. Zapewne nie bylibyśmy zadowoleni, gdyby precyzyjne informacje o naszych chorobach i tym, z kim i o czym dokładnie ostatnio rozmawialiśmy, stały się nagle publicznie dostępne. Powstaje więc pytanie: jak korzystać z danych prywatnych osób, aby ta prywatność nie została narażona na szwank?
Problem ten składa się w zasadzie z dwóch pytań: 1) jak przechowywać dane, by nie zostały one odczytane lub skradzione przez niepowołane osoby? oraz 2) jakie analizy przeprowadzać na danych, żeby opublikowanie nawet jedynie wyników tych analiz nie ujawniło prywatnych informacji? Nie będziemy się tu zajmować pytaniem 1, odpowiedzi w tym obszarze dostarcza klasyczna kryptografia. Zajmiemy się natomiast pytaniem 2 i zobaczymy, że odpowiedź na nie jest dalece nieoczywista.
Warto przyjrzeć się jakiemuś przykładowi, żebyśmy dobrze zrozumieli, na czym polega problem. Rozważymy przykład wzięty z rzeczywistości: firma Google zbiera dane na temat korków samochodowych powstających w dużych miastach. W tym celu śledzi m.in., gdzie i jak ja jeżdżę, w szczególności, o której danego dnia jechałem do pracy, o której z tej pracy wyszedłem, dokąd pojechałem itd. Możemy sobie wyobrazić, że firma Google nie tylko chce zbierać proste informacje o tym, że gdzieś często są korki, a gdzieś ich nie ma, ale może chciałaby też wiedzieć:
- Ile czasu średnio dziennie spędzają w korkach kobiety przed trzydziestką, a ile mężczyźni po sześćdziesiątce?
- Czy te same samochody stoją w korkach w różne dni tygodnia, czy może jest jakaś różnica pomiędzy początkiem tygodnia a końcem?
- Czy osoby mieszkające w danej okolicy radzą sobie lepiej w korkach powstających w tej okolicy i jeśli tak, to jak bardzo?
A dodatkowo Google z pewnością chce odpowiedzi na te pytania móc upublicznić. Nietrudno zgadnąć, że zbyt szczegółowe pytania tego rodzaju mogłyby ujawnić czyjąś prywatność. Przykładowo opublikowanie odpowiedzi na pytanie: Ile czasu w korkach w okolicy Mokotowa spędzają informatycy pracujący w Redakcji Delty? z pewnością narusza prywatność. A być może z wielu pytań o korki: w okolicy Wydziału MIM, w dzielnicy Mokotów, przed spotkaniem kolegium Delty itd., można by wywnioskować prawdopodobną odpowiedź na poprzednie pytanie. A zatem przy publikacji informacji musimy być rzeczywiście uważni.
Część Czytelników może pomyśleć w sposób, który jest dość powszechny: to żaden problem, wystarczy po prostu usunąć informacje, o kim są te dane. Niestety, nie jest tak prosto, już powyższy przykład co nieco o tym mówi. Nie wystarczy usunąć informacji, które jednoznacznie identyfikują daną osobę, takich jak powiedzmy imię, nazwisko, pesel, numer dowodu itd. Wiele innych danych przekazuje sporo informacji o nas, takich jak na przykład kod pocztowy, data urodzenia czy nawet tylko rok urodzenia. Okazuje się, że bardzo wiele osób można jednoznacznie zidentyfikować za pomocą trzech informacji: właśnie daty urodzenia, kodu pocztowego i płci. Żeby więc zanonimizować dane, trzeba by usunąć którąś z tych danych. Niestety podobnych zestawów informacji może być więcej, więc należałoby pousuwać więcej danych. A wtedy mogłoby się okazać, że to, co nam zostało, nie wystarcza do przeprowadzenia analizy, którą zaplanowaliśmy. W skrócie: nie tędy droga, a przynajmniej nie tędy wiedzie optymalna droga.
Zastanawiamy się już długo, jak by tu zachować prywatność poszczególnych osób, ale nie ustaliliśmy precyzyjnie, co w zasadzie oznacza, że raport z pewnej analizy zachowuje naszą prywatność. Zaproponujemy definicję, która wydaje się dobrze działać. Jej znalezienie okaże się dalece nieoczywiste. Pierwsza próba może być taka: (1) raport zachowuje moją prywatność, gdy czytający nie dowie się o mnie niczego. Wydaje się to jednak zbyt szeroka definicja. Ufoludek dowiadujący się, że średnia liczba rąk wśród ludzi zamieszkujących Ziemię wynosi 1,9999, dowie się, że ja najprawdopodobniej mam dwie ręce. Intuicyjnie rzecz biorąc, moja prywatność nie została jednak ujawniona w ten sposób, bo prywatne wydają się raczej te informacje, które odróżniają mnie od innych osób, a nie te, które są prawdziwe dla wszystkich ludzi. Może więc powinniśmy raczej powiedzieć, że: (2) raport zachowuje prywatność, jeśli odpowiedź na dowolne pytanie będzie dokładnie taka sama, gdy ja zostanę w nim uwzględniony i gdy zostanę pominięty. Dość łatwo jednak zauważyć, że każdy taki raport jest zupełnie bezwartościowy. Jeśli pominięcie jednej osoby nigdy niczego nie zmienia, to pominięcie wszystkich osób biorących udział w badaniach też nigdy niczego nie zmienia. Czyli takie wymaganie jest zbyt mocne. Żeby proponowane pojęcie miało sens, musimy wymaganie co do prywatności nieco osłabić. Być może wystarczy, jeżeli powiemy, że: (3) raport zachowuje prywatność, jeśli odpowiedź na dowolne pytanie zmieni się jedynie bardzo niewiele w zależności od tego, czy ja będę uwzględniony. Ta definicja wydaje się w porządku, ale zaraz zobaczymy, że zadając odpowiednio pytania, można ujawnić czyjeś prywatne dane. Powiedzmy, że została przeprowadzona ankieta wśród 1000 osób, w której każda z tych osób podała swoje miesięczne dochody. Następnie podane zostały dwie liczby: średnia dochodów wszystkich osób biorących udział w ankiecie 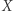 oraz średnia dochodów wszystkich osób oprócz autora tego artykułu
oraz średnia dochodów wszystkich osób oprócz autora tego artykułu 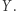 Jeśli ja w ogóle nie brałem udziału w ankiecie, to oczywiście
Jeśli ja w ogóle nie brałem udziału w ankiecie, to oczywiście 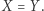 Jeśli jednak brałem udział w ankiecie, to wpływ moich dochodów na liczbę
Jeśli jednak brałem udział w ankiecie, to wpływ moich dochodów na liczbę 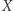 jest niewielki, a na liczbę
jest niewielki, a na liczbę 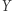 w ogóle żaden. Jednakże (o ile brałem udział w ankiecie) można łatwo odtworzyć moje dochody, które są równe
w ogóle żaden. Jednakże (o ile brałem udział w ankiecie) można łatwo odtworzyć moje dochody, które są równe 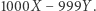 Widać więc, że ujawnianie dokładnych wyników jest niebezpieczne, nawet jeśli mój wpływ na nie jest bardzo mały, bo zadając kilka pytań, można odtworzyć prywatne dane. Musimy jakoś uniknąć tego przykrego efektu, w którym dwie ankiety, pozornie ujawniające niewiele informacji o nas, sumarycznie ujawniają ich bardzo dużo. Odpowiedzią jest więc podawanie danych przybliżonych - użyjemy do tego celu losowości. A zatem ostateczna propozycja to: (4) raport zachowuje prywatność, jeśli odpowiedź na każde pytanie TAK / NIE będzie z dużym prawdopodobieństwem taka sama, jeśli ja wezmę udział w badaniu i jeśli nie wezmę w nim udziału. Okazuje się, że jest to właściwe sformułowanie. A może nie tyle właściwe - bo jak właściwie możemy o tym rozstrzygać - co takie, które ma eleganckie własności teoretyczne i dobrze sprawdza się w praktyce.
Widać więc, że ujawnianie dokładnych wyników jest niebezpieczne, nawet jeśli mój wpływ na nie jest bardzo mały, bo zadając kilka pytań, można odtworzyć prywatne dane. Musimy jakoś uniknąć tego przykrego efektu, w którym dwie ankiety, pozornie ujawniające niewiele informacji o nas, sumarycznie ujawniają ich bardzo dużo. Odpowiedzią jest więc podawanie danych przybliżonych - użyjemy do tego celu losowości. A zatem ostateczna propozycja to: (4) raport zachowuje prywatność, jeśli odpowiedź na każde pytanie TAK / NIE będzie z dużym prawdopodobieństwem taka sama, jeśli ja wezmę udział w badaniu i jeśli nie wezmę w nim udziału. Okazuje się, że jest to właściwe sformułowanie. A może nie tyle właściwe - bo jak właściwie możemy o tym rozstrzygać - co takie, które ma eleganckie własności teoretyczne i dobrze sprawdza się w praktyce.
Propozycja ta została wysunięta w artykule Dwork, McSherry'ego, Nissima i Smitha: Calibrating Noise to Sensitivity in Private Data Analysis opublikowanym w 2006 roku. Za pracę tę i wprowadzone w niej pojęcie prywatności różnicowej (differential privacy) autorzy otrzymali w 2017 roku Nagrodę Gödla, najbardziej prestiżową nagrodę przyznawaną w informatyce teoretycznej. Powyżej starałem się przekazać pewne intuicje, które mogły doprowadzić do takiej właśnie definicji. Teraz przyjrzyjmy się samemu pojęciu. Niech 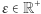 będzie dodatnią liczbą rzeczywistą, a
będzie dodatnią liczbą rzeczywistą, a 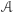 algorytmem randomizowanym (tj. używającym losowości), który dla bazy danych
algorytmem randomizowanym (tj. używającym losowości), który dla bazy danych 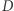 zwraca odpowiedź
zwraca odpowiedź 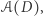 należącą do zbioru wszystkich możliwych raportów
należącą do zbioru wszystkich możliwych raportów 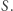 Powiemy, że algorytm
Powiemy, że algorytm 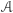 jest
jest  -różnicowo-prywatny, jeśli dla dowolnych dwóch baz danych
-różnicowo-prywatny, jeśli dla dowolnych dwóch baz danych 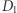 oraz
oraz 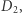 które różnią się jednym elementem (np. danymi jednej osoby), oraz dla dowolnego zbioru możliwych wyników
które różnią się jednym elementem (np. danymi jednej osoby), oraz dla dowolnego zbioru możliwych wyników 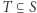 zachodzi
zachodzi
![P[𝒜(D1) ∈ T] ⩽ eε⋅P[𝒜(D2) ∈T ],](/math/temat/matematyka/kryptologia/2020/08/25/prywatnosc-w-morzu-danych/11x-c862724872ac0ae9a368627099b1fab521e8c1bb-dm-33,33,33-FF,FF,FF.gif) |
gdzie przez ![P[X]](/math/temat/matematyka/kryptologia/2020/08/25/prywatnosc-w-morzu-danych/12x-c862724872ac0ae9a368627099b1fab521e8c1bb-im-33,33,33-FF,FF,FF.gif) oznaczamy prawdopodobieństwo zdarzenia
oznaczamy prawdopodobieństwo zdarzenia 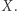 Przypomnijmy, że dla małych
Przypomnijmy, że dla małych 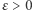 wartość
wartość 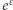 jest bardzo bliska
jest bardzo bliska 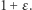 Zauważmy też, że ta sama nierówność zachodzi, gdy zamienimy
Zauważmy też, że ta sama nierówność zachodzi, gdy zamienimy 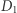 i
i 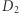 miejscami, więc intuicyjnie możemy myśleć, że liczby
miejscami, więc intuicyjnie możemy myśleć, że liczby ![|P[𝒜(D1) ∈ T]](/math/temat/matematyka/kryptologia/2020/08/25/prywatnosc-w-morzu-danych/19x-c862724872ac0ae9a368627099b1fab521e8c1bb-im-33,33,33-FF,FF,FF.gif) oraz
oraz ![P[𝒜(D2) ∈ T]](/math/temat/matematyka/kryptologia/2020/08/25/prywatnosc-w-morzu-danych/20x-c862724872ac0ae9a368627099b1fab521e8c1bb-im-33,33,33-FF,FF,FF.gif) są równe z dokładnością do czynnika
są równe z dokładnością do czynnika 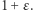
Dobrze, ale dlaczego pojęcie  -prywatności różnicowej zostało aż tak bardzo docenione? Jest to bardzo dobra miara ilości ujawnionej prywatności, w domyśle właśnie
-prywatności różnicowej zostało aż tak bardzo docenione? Jest to bardzo dobra miara ilości ujawnionej prywatności, w domyśle właśnie  Zauważmy, że spełnia ono nasze wymaganie (4). Istotnie, baza danych
Zauważmy, że spełnia ono nasze wymaganie (4). Istotnie, baza danych 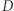 bez moich danych oraz baza danych
bez moich danych oraz baza danych 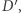 która powstała przez dodanie do bazy danych
która powstała przez dodanie do bazy danych 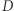 moich danych, różnią się jedynie jednym elementem. Dowolne pytanie na temat bazy danych
moich danych, różnią się jedynie jednym elementem. Dowolne pytanie na temat bazy danych 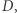 na które odpowiedź jest TAK lub NIE, musi tak naprawdę być postaci: czy nasz raport
na które odpowiedź jest TAK lub NIE, musi tak naprawdę być postaci: czy nasz raport 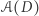 należy do wyróżnionego zbioru raportów
należy do wyróżnionego zbioru raportów 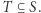 A więc, istotnie, dla każdego pytania prawdopodobieństwo odpowiedzi TAK tylko nieznacznie się zmieni (maksymalnie o około
A więc, istotnie, dla każdego pytania prawdopodobieństwo odpowiedzi TAK tylko nieznacznie się zmieni (maksymalnie o około  ) w zależności od tego, czy ja będę uczestniczył w badaniu, czy też nie. Pojęcie prywatności różnicowej unika przykrej własności, którą miała definicja z punktu (3). Mianowicie jeśli zrobimy kilka badań dobrze zachowujących prywatność, to sumarycznie ujawnią one również niewiele prywatności. Łatwo udowodnić, co polecamy Czytelnikowi, że jeśli stworzymy
) w zależności od tego, czy ja będę uczestniczył w badaniu, czy też nie. Pojęcie prywatności różnicowej unika przykrej własności, którą miała definicja z punktu (3). Mianowicie jeśli zrobimy kilka badań dobrze zachowujących prywatność, to sumarycznie ujawnią one również niewiele prywatności. Łatwo udowodnić, co polecamy Czytelnikowi, że jeśli stworzymy 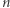 badań, o prywatności różnicowej odpowiednio
badań, o prywatności różnicowej odpowiednio 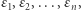 to sumarycznie to badanie będzie miało prywatność różnicową nie większą niż
to sumarycznie to badanie będzie miało prywatność różnicową nie większą niż 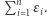 Czyli intuicja mówiąca o tym, że algorytm
Czyli intuicja mówiąca o tym, że algorytm  -różnicowo-prywatny "ujawnia
-różnicowo-prywatny "ujawnia  prywatności", jest dobra - ta miara się sumuje. Oprócz innych zalet tego pojęcia być może najważniejszą jest to, że można stosunkowo łatwo zaprojektować system, który je realizuje. Idea jest bardzo naturalna, po prostu do wyniku zapytania na prawdziwej bazie danych dodaje się losowy szum i dopiero ten zaszumiony wynik się publikuje. Jest wiele różnych mechanizmów realizacji tego pomysłu, bo np. warto inaczej traktować zapytania
prywatności", jest dobra - ta miara się sumuje. Oprócz innych zalet tego pojęcia być może najważniejszą jest to, że można stosunkowo łatwo zaprojektować system, który je realizuje. Idea jest bardzo naturalna, po prostu do wyniku zapytania na prawdziwej bazie danych dodaje się losowy szum i dopiero ten zaszumiony wynik się publikuje. Jest wiele różnych mechanizmów realizacji tego pomysłu, bo np. warto inaczej traktować zapytania 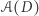 zwracające liczby rzeczywiste, a inaczej takie, które przyjmują tylko skończenie wiele możliwych wartości. Najbardziej znany mechanizm nazywa się mechanizmem Laplace'a i dobrze zachowuje się w sytuacji, gdy
zwracające liczby rzeczywiste, a inaczej takie, które przyjmują tylko skończenie wiele możliwych wartości. Najbardziej znany mechanizm nazywa się mechanizmem Laplace'a i dobrze zachowuje się w sytuacji, gdy 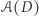 przyjmuje wartości rzeczywiste z pewnym rozkładem ciągłym. Do wyniku dodaje się w nim zmienną o rozkładzie Laplace'a
przyjmuje wartości rzeczywiste z pewnym rozkładem ciągłym. Do wyniku dodaje się w nim zmienną o rozkładzie Laplace'a 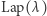 :
:
Jeśli 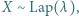 to gęstość zmiennej
to gęstość zmiennej 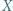 wyraża się wzorem
wyraża się wzorem 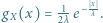
Zainteresowanego Czytelnika zachęcam do zgłębiania szczegółów. Mimo że pojęcie prywatności różnicowej jest stosunkowo nowe, to w Internecie można o nim znaleźć wiele wartościowych informacji.
Na koniec warto powiedzieć, że pojęcie prywatności różnicowej bardzo szybko zdobywa popularność. Już teraz wielkie firmy technologiczne, takie jak Google, Apple, Microsoft czy Facebook, zaczynają go używać w swoich zastosowaniach. Przykładowo Google stosuje prywatność różnicową przy analizie złośliwego oprogramowania w przeglądarce Chrome i korków w dużych miastach w aplikacji Maps, a Apple przy analizie użycia emotikonów w różnych kontekstach oraz słów niewystępujących w słowniku. Wiele uniwersytetów dodaje do swoich kursów materiały na ten temat. Całkiem prawdopodobne, że jesteśmy w przededniu dużego sukcesu tego pojęcia.