A jednak się da!
O obliczeniach wielopodmiotowych (AJSD IX)
Niniejszy odcinek jest ostatni z serii. Przez niemal rok, wraz z Łukaszem Rajkowskim, próbowaliśmy pokazać Czytelnikowi, co ciekawego, a przede wszystkim - co zaskakującego, wiąże się z kryptologią. Naszą wielką nagrodą będzie, gdy - po przeczytaniu tych 9 odcinków - choć niewielka część Czytelników chociaż przez chwilę zawaha się, gdy w życiu codziennym będzie stwierdzać, że czegoś się nie da...
Punktem wyjścia naszych rozważań będzie podział sekretu pomiędzy 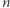 osób (o którym pisaliśmy więcej w
osób (o którym pisaliśmy więcej w 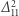 ). To znaczy: załóżmy, że chcemy pewną tajną liczbę
). To znaczy: załóżmy, że chcemy pewną tajną liczbę

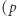 to pewna ustalona duża liczba pierwsza, np.
to pewna ustalona duża liczba pierwsza, np. 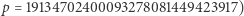 rozproszyć pomiędzy zbiór osób
rozproszyć pomiędzy zbiór osób 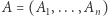 w taki sposób, aby:
w taki sposób, aby:
- każda z nich dostała pewien udział w postaci liczby
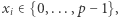 oraz
oraz - dowolna ich
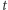 -osobowa podgrupa nie była w stanie odtworzyć
-osobowa podgrupa nie była w stanie odtworzyć 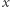 (analizując swoje udziały), ale już (każda) podgrupa
(analizując swoje udziały), ale już (każda) podgrupa 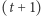 -osobowa zawsze mogła to zrobić.
-osobowa zawsze mogła to zrobić.
Powyższy problem da się rozwiązać dla dowolnego 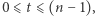 szczegóły znajdują się w artykule cytowanym wyżej. Ogólna idea (pochodząca od Adiego Shamira) polega na tym, że losujemy dowolny wielomian
szczegóły znajdują się w artykule cytowanym wyżej. Ogólna idea (pochodząca od Adiego Shamira) polega na tym, że losujemy dowolny wielomian 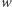 stopnia
stopnia 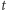 (o współczynnikach
(o współczynnikach 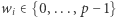 ) o wyrazie wolnym równym
) o wyrazie wolnym równym  Następnie ustalamy dowolne niezerowe (i parami różne) elementy
Następnie ustalamy dowolne niezerowe (i parami różne) elementy 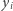 i określamy
i określamy

Okazuje się, że tak zdefiniowane udziały spełniają nasze pierwotne założenia. Dziś jednak będziemy chcieli osiągnąć znacznie więcej. To znaczy, zapragniemy na podzielonych sekretach rachować!
Przyjmijmy, że sekrety są dwa: 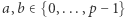 oraz że osoba o numerze
oraz że osoba o numerze 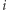 ma udziały w obu (w postaci liczb
ma udziały w obu (w postaci liczb 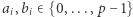 ). Chcemy teraz opracować taki protokół, który umożliwi wszystkim
). Chcemy teraz opracować taki protokół, który umożliwi wszystkim  osobom dokonanie wspólnych obliczeń, po których osoba
osobom dokonanie wspólnych obliczeń, po których osoba 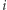 otrzyma pewną wartość
otrzyma pewną wartość 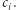 Oczekujemy, że tak obliczone elementy
Oczekujemy, że tak obliczone elementy 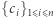 razem będą stanowić podział sekretu dla (rozważamy trzy przypadki):
razem będą stanowić podział sekretu dla (rozważamy trzy przypadki):
- 1.
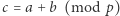 ;
;- 2.
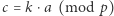
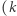 jest publicznie znaną stałą);
jest publicznie znaną stałą);- 3.
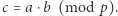
Banalne rozwiązanie polega na odtworzeniu 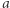 i
i 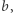 obliczeniu
obliczeniu  oraz dokonaniu nowego podziału, według oryginalnego protokołu. Nasz cel jest jednak ambitniejszy: chcemy rozproszyć
oraz dokonaniu nowego podziału, według oryginalnego protokołu. Nasz cel jest jednak ambitniejszy: chcemy rozproszyć 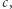 ale w taki sposób, aby bezpośrednia informacja o
ale w taki sposób, aby bezpośrednia informacja o  i
i 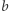 nie została na żadnym etapie przez nikogo (przez żadnego uczestnika bądź ich podgrupy o ograniczonej liczebności) jawnie odtworzona. Jak to zrobić?
nie została na żadnym etapie przez nikogo (przez żadnego uczestnika bądź ich podgrupy o ograniczonej liczebności) jawnie odtworzona. Jak to zrobić?
Przypadek pierwszy i drugi jest łatwy (Zajmiemy się tylko pierwszym. Niech drugi pozostanie jako łatwe ćwiczenie.) i nie wymaga nawet żadnej komunikacji pomiędzy stronami. Wystarczy, że osoba 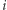 przyjmie
przyjmie 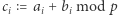 i wszystko będzie w porządku. Dlaczego? Przypomnijmy sobie tylko, czym jest
i wszystko będzie w porządku. Dlaczego? Przypomnijmy sobie tylko, czym jest 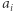 oraz
oraz 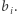 Wiemy przecież, że
Wiemy przecież, że

dla pewnych wielomianów 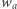 oraz
oraz 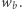 Wtedy oczywiście
Wtedy oczywiście

co oznacza, że (z definicji) elementy 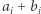 stanowią podział sekretu dla wyrazu wolnego wielomianu
stanowią podział sekretu dla wyrazu wolnego wielomianu 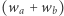 modulo
modulo 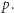 Ten jednak wynosi
Ten jednak wynosi 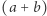 modulo
modulo 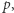 gdyż wyrazem wolnym
gdyż wyrazem wolnym 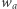 musi być
musi być 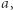 a wyrazem wolnym
a wyrazem wolnym 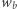 jest
jest 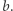
Powyższe rozwiązanie rodzi pokusę, aby analogicznie rozwiązać przypadek trzeci. To znaczy, aby każda z osób przyjęła 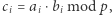 jako że
jako że 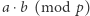 jest wyrazem wolnym wielomianu
jest wyrazem wolnym wielomianu  modulo
modulo 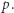 Niestety, jest to rozwiązanie błędne. Problem bierze się stąd, że mnożenie dwóch wielomianów stopnia
Niestety, jest to rozwiązanie błędne. Problem bierze się stąd, że mnożenie dwóch wielomianów stopnia 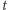 daje wielomian stopnia
daje wielomian stopnia 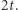 A my przecież chcemy koniecznie otrzymać stopień
A my przecież chcemy koniecznie otrzymać stopień 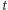 (w przypadku dodawania ten problem nie występował)! Rozwiązanie jest tutaj nieco bardziej skomplikowane.
(w przypadku dodawania ten problem nie występował)! Rozwiązanie jest tutaj nieco bardziej skomplikowane.
Mnożenie podzielonych sekretów
Pierwszy krok jest taki sam, jak w naiwnym rozwiązaniu wyżej. To znaczy, faktycznie każdy z uczestników protokołu mnoży 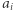 przez
przez 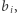 otrzymując pewne
otrzymując pewne 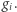 Zanim przejdziemy do szczegółów kolejnego kroku, potrzebujemy jeszcze kilku oznaczeń. Oznaczmy więc wielomian
Zanim przejdziemy do szczegółów kolejnego kroku, potrzebujemy jeszcze kilku oznaczeń. Oznaczmy więc wielomian 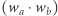 modulo
modulo 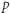 przez
przez 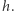 Wówczas wyraz wolny
Wówczas wyraz wolny 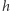 to
to 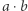 modulo
modulo 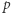 (tak jak potrzeba), natomiast wartość
(tak jak potrzeba), natomiast wartość 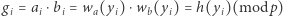 jest znana osobie
jest znana osobie 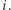 Problemem jest tylko stopień wielomianu
Problemem jest tylko stopień wielomianu

który wynosi 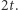 Wprowadźmy więc (trochę na siłę) nowy wielomian:
Wprowadźmy więc (trochę na siłę) nowy wielomian:

który powstał przez zwykłe wymazanie ostatnich 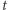 jednomianów wielomianu
jednomianów wielomianu 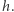 Byłoby oczywiście świetnie, gdyby osoba
Byłoby oczywiście świetnie, gdyby osoba 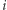 potrafiła (za pomocą jakiegoś protokołu) po prostu bezpiecznie obliczyć wartość
potrafiła (za pomocą jakiegoś protokołu) po prostu bezpiecznie obliczyć wartość 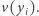 Okazuje się, że jest to wykonalne! Co więcej, nie aż tak trudne obliczeniowo i nie wymaga dużej komunikacji między uczestnikami protokołu. Kluczowa jest tu (dość zaskakująca) obserwacja, że każde
Okazuje się, że jest to wykonalne! Co więcej, nie aż tak trudne obliczeniowo i nie wymaga dużej komunikacji między uczestnikami protokołu. Kluczowa jest tu (dość zaskakująca) obserwacja, że każde 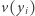 jest kombinacją liniową elementów
jest kombinacją liniową elementów 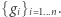
Gdy już to wiemy, to dalej jest z górki. Dodawanie i mnożenie przez stałą sekretów potrafimy już wykonywać. Trzeba więc tylko rozproszyć każde 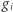 i zastosować (być może wielokrotnie) dwa proste przypadki rozważane wyżej (oraz na koniec wysłać osobie
i zastosować (być może wielokrotnie) dwa proste przypadki rozważane wyżej (oraz na koniec wysłać osobie 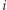 odpowiednie udziały do odtworzenia
odpowiednie udziały do odtworzenia 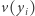 ). Dokładne wyjaśnienie, ze względu na techniczny charakter zagadnienia, musimy niestety pominąć. Wierzymy jednak, że dokładne odtworzenie wszystkich kroków tego przypadku może być bardzo pouczające. Szczegóły znajdują się w pracy "A Full Proof of the BGW Protocol for Perfectly-secure Multiparty Computation" autorstwa Gilada Asharova oraz Yehudy Lindella.
). Dokładne wyjaśnienie, ze względu na techniczny charakter zagadnienia, musimy niestety pominąć. Wierzymy jednak, że dokładne odtworzenie wszystkich kroków tego przypadku może być bardzo pouczające. Szczegóły znajdują się w pracy "A Full Proof of the BGW Protocol for Perfectly-secure Multiparty Computation" autorstwa Gilada Asharova oraz Yehudy Lindella.
Po co to wszystko?!
Przyjmijmy, że każda z osób 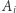 wybrała swój własny argument
wybrała swój własny argument 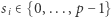 i rozproszyła go wśród wszystkich pozostałych osób. Co umożliwiają nam protokoły naszkicowane wyżej? Otóż na pewno grupa może (wspólnie) obliczyć chociażby
i rozproszyła go wśród wszystkich pozostałych osób. Co umożliwiają nam protokoły naszkicowane wyżej? Otóż na pewno grupa może (wspólnie) obliczyć chociażby 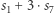 modulo
modulo 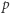 czy
czy 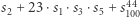 modulo
modulo 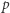 (w taki sposób, że żadne obliczenia pośrednie nie są nikomu znane - wszak wszystko odbywa się dla rozproszonych wartości), bo potrafi dodawać, skalować przez stałą i mnożyć sekrety. Jak wiele w taki sposób można policzyć? Okazuje się, że … wszystko!
(w taki sposób, że żadne obliczenia pośrednie nie są nikomu znane - wszak wszystko odbywa się dla rozproszonych wartości), bo potrafi dodawać, skalować przez stałą i mnożyć sekrety. Jak wiele w taki sposób można policzyć? Okazuje się, że … wszystko!
Obliczenia w ciele modulo 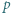 mają taką cechę, że każdą funkcję (oczywiście o zbiorze wartości
mają taką cechę, że każdą funkcję (oczywiście o zbiorze wartości 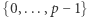 ) da się zapisać jako wielomian, a więc jako złożenie (być może bardzo wielu) dodawań, skalowań przez stałą i mnożeń (wszystko modulo
) da się zapisać jako wielomian, a więc jako złożenie (być może bardzo wielu) dodawań, skalowań przez stałą i mnożeń (wszystko modulo 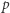 ). Innymi słowy: z faktu, że znamy protokoły dla trzech przypadków z pierwszej części artykułu, wynika, że potrafimy obliczyć zupełnie dowolną funkcję rozproszonych argumentów. Stąd już tylko krok do protokołów na np. granie w pokera przez Internet bez zaufanej strony czy bezpieczne aukcje internetowe bez serwera zbierającego i w zaufaniu porównującego oferty.
). Innymi słowy: z faktu, że znamy protokoły dla trzech przypadków z pierwszej części artykułu, wynika, że potrafimy obliczyć zupełnie dowolną funkcję rozproszonych argumentów. Stąd już tylko krok do protokołów na np. granie w pokera przez Internet bez zaufanej strony czy bezpieczne aukcje internetowe bez serwera zbierającego i w zaufaniu porównującego oferty.
Science-fiction
Wyżej ledwie naszkicowaliśmy ideę obliczeń wielopodmiotowych (i to jeszcze w mniej ciekawym, bo pasywnym przypadku - szczegóły na jednym z marginesów). Póki co nie są one jeszcze bardzo praktyczne, ale powoli zbliżamy się do momentu, gdy (na razie) proste ich zastosowania będą możliwe do codziennego wykorzystania. Chcielibyśmy jednak mocno zaznaczyć, że drzemie w nich potencjał niemal rewolucyjny.
Rozpraszanie obliczeń i przechowywania danych czy ogólniej - pozbywanie się zaufanych stron z cyfrowego świata jest wszak (skromnym zdaniem autora tego tekstu) najważniejszym wyzwaniem rewolucji cyfrowej XXI wieku.
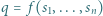 , to mamy na myśli, że każdy z uczestników protokołu po jego zakończeniu pozna pewne
, to mamy na myśli, że każdy z uczestników protokołu po jego zakończeniu pozna pewne 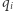 takie, że wszystkie
takie, że wszystkie 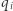 razem stanowią podział
razem stanowią podział 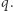 Następnie wszyscy powinni upublicznić swoje
Następnie wszyscy powinni upublicznić swoje 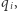 aby każdy uczestnik mógł faktycznie poznać wartość
aby każdy uczestnik mógł faktycznie poznać wartość 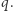 Kluczową cechą tego protokołu jest, że rzeczywiście jedyną nową informacją na temat
Kluczową cechą tego protokołu jest, że rzeczywiście jedyną nową informacją na temat 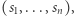 którą pozna każdy z jego uczestników, jest właśnie
którą pozna każdy z jego uczestników, jest właśnie 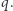 Wszelkie informacje pośrednie pozostaną tajne.
Wszelkie informacje pośrednie pozostaną tajne.