A jednak się da!
Odtajniamy transfer utajniony (AJSD IV)
Ence-pence w której ręce? - za moich dziecięcych lat przedstawiona formułka, której towarzyszyły często dwie wyciągnięte przez wypowiadającą ją osobę ręce, była zwiastunem jakiejś bardzo przyjemnej (najczęściej słodkiej) niespodzianki. Każda wyciągnięta dłoń skrywała bowiem coś dobrego, jednak jako szkrab i tak poświęcałem chwilę zastanowienia nad jej wyborem, będąc świadomym ryzyka, że niewskazana przeze mnie ręka zawiera bardziej atrakcyjny podarek i powędruje on do mojego brata.
Ta dziecięca wyliczanka będzie dla nas punktem wyjścia do rozważań nad problemem pozornie niemającym zastosowania w rzeczywistości. Zapytajmy bowiem, czy dziecko jest w stanie dowiedzieć się, co znajduje się w wybranej przez nie ręce, tak aby spełnione były dwa warunki:
- (1)
- dziecko nie dowiaduje się, co znajduje się w drugiej ręce rodzica,
- (2)
- rodzic nie dowiaduje się, którą rękę wybrało dziecko.
Powyższe założenia wydają się sprzeczne, a procedura, która miałaby je spełniać, zakrawa o sztuczkę magiczną. Jest to jednak możliwe - stosowny protokół nazywa się transferem utajnionym. Pisał o nim Tomasz Kazana w Delcie 5/2012. Transfer utajniony jest jednak na tyle ważną "cegiełką" kryptograficzną, że dla pełności naszego cyklu postanowiliśmy przypomnieć go w tym krótkim artykule.
Rozpocznijmy od przedstawienia naszego problemu w bardziej matematycznym języku. Aby biedny rodzic nie musiał utrzymywać przez cały czas rąk w górze, załóżmy, że przyporządkowuje on wartości dwóm zmiennym: 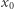 (lewa ręka) i
(lewa ręka) i 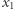 (prawa ręka); dla ułatwienia opisu załóżmy, że wartości te są liczbami naturalnymi. Dziecko wybiera natomiast
(prawa ręka); dla ułatwienia opisu załóżmy, że wartości te są liczbami naturalnymi. Dziecko wybiera natomiast 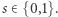 Jego zadaniem jest poznanie wartości
Jego zadaniem jest poznanie wartości 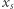 bez ujawniania
bez ujawniania 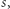 natomiast rodzic nie może wyjawić wartości
natomiast rodzic nie może wyjawić wartości 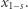
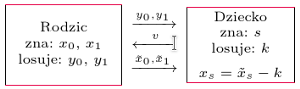
Schemat przesyłu informacji między rodzicem i dzieckiem.
Pierwszym krokiem protokołu jest stworzenie bazy do szyfrowania z kluczem publicznym, tak jak opisane to zostało w pierwszym odcinku serii, opublikowanym w Delcie 10/2018. Rodzic wybiera dwie duże liczby pierwsze 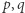 tak, aby
tak, aby 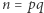 było większe od każdej z liczb
było większe od każdej z liczb 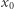 i
i 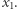 Następnie rodzic oblicza
Następnie rodzic oblicza 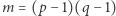 i znajduje takie dwie liczby naturalne
i znajduje takie dwie liczby naturalne  i
i 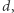 że
że 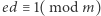 (tzn.
(tzn. 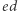 daje resztę 1 z dzielenia przez
daje resztę 1 z dzielenia przez 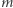 ). Ponadto rodzic losuje liczby
). Ponadto rodzic losuje liczby 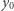 i
i 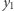 i wyjawia dziecku wartość każdej z nich. Dziecko natomiast losuje liczbę
i wyjawia dziecku wartość każdej z nich. Dziecko natomiast losuje liczbę 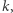 której nigdy nie ujawni rodzicowi. Zamiast tego przesyła mu wartość
której nigdy nie ujawni rodzicowi. Zamiast tego przesyła mu wartość 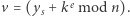 Na jej podstawie rodzic oblicza
Na jej podstawie rodzic oblicza 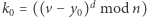 oraz
oraz 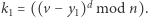 Zauważmy, że wówczas
Zauważmy, że wówczas 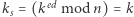 (po szczegóły odsyłamy do pierwszej części sagi). Jeśli zatem rodzic prześle dziecku wartości
(po szczegóły odsyłamy do pierwszej części sagi). Jeśli zatem rodzic prześle dziecku wartości 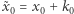 oraz
oraz 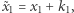 to dziecko będzie mogło obliczyć wartość
to dziecko będzie mogło obliczyć wartość 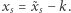
Wiemy już, że w opisany wyżej sposób dziecko poznaje wartość 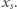 Jedyna informacja, jaką rodzic dostaje od dziecka, to wartość
Jedyna informacja, jaką rodzic dostaje od dziecka, to wartość  Na jej podstawie rodzic nie jest w stanie powiedzieć niczego o
Na jej podstawie rodzic nie jest w stanie powiedzieć niczego o  ze względu na losowy wybór
ze względu na losowy wybór 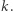 Pozostaje wykazać, że dziecko nie jest w stanie obliczyć wartości
Pozostaje wykazać, że dziecko nie jest w stanie obliczyć wartości 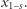 Zauważmy, że
Zauważmy, że
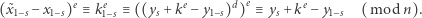 |
Ponieważ 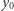 i
i 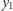 były losowane przez rodzica, to z punktu widzenia dziecka liczba
były losowane przez rodzica, to z punktu widzenia dziecka liczba 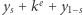 jest losowa. Gdyby dziecko potrafiło obliczyć
jest losowa. Gdyby dziecko potrafiło obliczyć 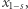 to ponieważ zna
to ponieważ zna 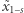 - potrafiłoby obliczyć lewą stronę powyższej równości. Rozwiązałoby zatem równanie
- potrafiłoby obliczyć lewą stronę powyższej równości. Rozwiązałoby zatem równanie 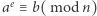 dla losowo wybranej wartości
dla losowo wybranej wartości 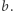 Z pierwszego odcinka sagi wiemy, że zadanie to jest równie trudne, co złamanie szyfru RSA, jeśli zatem wierzymy w bezpieczeństwo tego ostatniego, nie powinniśmy mieć skrupułów w używaniu przedstawionego protokołu transferu ujawnionego. A o tym, że kryptologia opiera się na wierze (lecz również zrozumieniu!) pisaliśmy już w Delcie niejednokrotnie...
Z pierwszego odcinka sagi wiemy, że zadanie to jest równie trudne, co złamanie szyfru RSA, jeśli zatem wierzymy w bezpieczeństwo tego ostatniego, nie powinniśmy mieć skrupułów w używaniu przedstawionego protokołu transferu ujawnionego. A o tym, że kryptologia opiera się na wierze (lecz również zrozumieniu!) pisaliśmy już w Delcie niejednokrotnie...