A jednak się da!
O kryptografii klucza publicznego i podpisie cyfrowym (AJSD I)
Problem szyfrowania przesyłanych wiadomości sięga jeszcze czasów starożytnych, więc naszego nowego deltowego cyklu artykułów o kryptologii prezentowanego w rubryce "A jednak się da!" nie możemy nie zacząć od przypomnienia najstarszego znanego systemu szyfrowania, mianowicie szyfru Cezara. Szyfr ten nie jest specjalnie wyrafinowany...
Po prostu umawiamy się, że (na przykład) zamiast litery A będziemy pisać G; zamiast B - literę H; zamiast C - literę I i tak dalej, to znaczy: zamiast  -tej litery alfabetu będziemy pisać
-tej litery alfabetu będziemy pisać 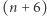 -tą literę. (Tak naprawdę
-tą literę. (Tak naprawdę 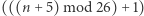 -tą literę, gdyż pod koniec musimy alfabet cyklicznie zawinąć do początku.) Równie dobrze moglibyśmy alfabet przesuwać nie o 6 pozycji, a o 3 pozycje, o 17 pozycji, czy ogólnie: o
-tą literę, gdyż pod koniec musimy alfabet cyklicznie zawinąć do początku.) Równie dobrze moglibyśmy alfabet przesuwać nie o 6 pozycji, a o 3 pozycje, o 17 pozycji, czy ogólnie: o 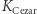 pozycji.
pozycji.
Nieco bardziej skomplikowany jest szyfr permutacyjny. Tutaj dwie strony ustalają zawczasu permutację literek

a następnie - aby zaszyfrować tekst - przykładają tę permutację do kolejnych literek wiadomości, uzyskując szyfrogram, czyli tekst zaszyfrowany. Odszyfrowanie wygląda podobnie, tylko przykładamy kolejno permutację odwrotną do 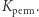
Oba powyższe przykłady wpisują się w pewien bardzo ogólny schemat szyfrowania. Mianowicie, na początku, jeszcze przed jakimkolwiek szyfrowaniem, dwie strony (ochrzcijmy je imionami Aldona i Bogumił) muszą się spotkać i ustalić coś sekretnego, czyli tak zwany klucz kryptograficzny 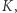 w naszym przykładach, odpowiednio:
w naszym przykładach, odpowiednio: 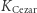 oraz
oraz 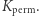 Następnie, gdy Aldona chce przekazać Bogumiłowi wiadomość
Następnie, gdy Aldona chce przekazać Bogumiłowi wiadomość 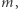 musi ona najpierw obliczyć wartość
musi ona najpierw obliczyć wartość 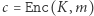 (gdzie
(gdzie 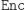 jest specyficznym opisem wybranego szyfru) i wysłać właśnie ją do Bogumiła. Bogumił otrzymawszy szyfrogram
jest specyficznym opisem wybranego szyfru) i wysłać właśnie ją do Bogumiła. Bogumił otrzymawszy szyfrogram 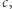 dokonuje obliczenia
dokonuje obliczenia 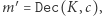 gdzie
gdzie 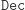 oznacza funkcję deszyfrującą. Oczywiście, żeby wszystko miało ręce i nogi, musi zawsze (dla każdego wyboru
oznacza funkcję deszyfrującą. Oczywiście, żeby wszystko miało ręce i nogi, musi zawsze (dla każdego wyboru 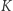 ) zachodzić
) zachodzić 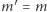 oraz - ze względów bezpieczeństwa - podsłuchanie szyfrogramu
oraz - ze względów bezpieczeństwa - podsłuchanie szyfrogramu  przez niecną Helgę nie może ujawnić właściwego komunikatu, czyli
przez niecną Helgę nie może ujawnić właściwego komunikatu, czyli 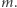 Ten ostatni wymóg nie jest wcale banalny do sformalizowania, ale my pozostaniemy przy nieformalnym określeniu - chcemy po prostu, aby dla Helgi było bardzo trudno wywnioskować cokolwiek na temat
Ten ostatni wymóg nie jest wcale banalny do sformalizowania, ale my pozostaniemy przy nieformalnym określeniu - chcemy po prostu, aby dla Helgi było bardzo trudno wywnioskować cokolwiek na temat 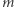 z wartości
z wartości 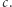 Dodatkowo w środowisku kryptologicznym przyjmuje się, że Helga zawsze wie, jakiego systemu używają Aldona z Bogumiłem - innymi słowy zna definicję
Dodatkowo w środowisku kryptologicznym przyjmuje się, że Helga zawsze wie, jakiego systemu używają Aldona z Bogumiłem - innymi słowy zna definicję 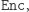 a jedyne czego nie zna, to klucz
a jedyne czego nie zna, to klucz 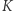 (to założenie to treść tak zwanej zasady Kerckhoffsa). Więcej o samej zasadzie Kerckhoffsa oraz motywacji jej przyjęcia pisaliśmy w Migawce w Delcie 07/2018
(to założenie to treść tak zwanej zasady Kerckhoffsa). Więcej o samej zasadzie Kerckhoffsa oraz motywacji jej przyjęcia pisaliśmy w Migawce w Delcie 07/2018
Przez setki lat rozwój kryptologii przebiegał dokładnie według powyższego schematu. Wymyślano przeróżne szyfry, po czym próbowano się upewnić, czy aby na pewno znajomość 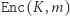 (oraz definicji
(oraz definicji 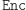 ) nic nie mówi o
) nic nie mówi o 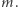 Okazało się dość szybko, że zarówno szyfr Cezara, jak i permutacyjny, nie są bezpiecznymi szyframi, ale za to inne współczesne szyfry, np. AES czy Triple-DES, uchodzą za bezpieczne i są stosowane powszechnie do dziś.
Okazało się dość szybko, że zarówno szyfr Cezara, jak i permutacyjny, nie są bezpiecznymi szyframi, ale za to inne współczesne szyfry, np. AES czy Triple-DES, uchodzą za bezpieczne i są stosowane powszechnie do dziś.
Wszystko pięknie, ale widać, gdzie znajduje się spora niewygoda. Żeby szyfrować, trzeba bezpiecznie ustalić wspólny tajny klucz. Zadanie to wcale nie wydaje się banalne (szczególnie, gdy Aldona i Bogumił mieszkają na różnych kontynentach, trwa wojna etc.), więc można by sformułować następujące naiwne marzycielskie pytanie:
Czy da się skonstruować szyfr taki, który nie wymaga ustalania wspólnego tajnego klucza, to znaczy, aby po prostu 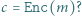
Łatwo wykazać, że postulat powyższy nie jest możliwy do zrealizowania.
Dowód. Załóżmy przeciwnie, a więc, że takie 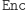 istnieje. Wówczas:
istnieje. Wówczas:
- (1)
- Oczywiście Bogumił musi być w stanie deszyfrować przychodzące do niego szyfrogramy, a więc:
- (2)
- Istnieje taka funkcja
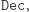 że
że 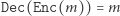 ; oznacza to, że:
; oznacza to, że: - (3)
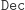 jest funkcją odwrotną do
jest funkcją odwrotną do 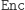 ; pamiętajmy, że:
; pamiętajmy, że:- (4)
- Helga zna definicję
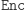 (zasada Kerckhoffsa).
(zasada Kerckhoffsa). - (5)
- Wystarczy więc, że Helga obliczy funkcję odwrotną do (znanej jej!) funkcji
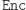 i już jest w stanie robić to, co Bogumił, czyli deszyfrować.
i już jest w stanie robić to, co Bogumił, czyli deszyfrować. - (6)
- Niestety, oznacza to, że szyfrowanie
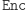 nie jest bezpieczne, co kończy dowód.
nie jest bezpieczne, co kończy dowód.

Pomimo znajomości powyższego rozumowania w roku 1976 dwóch dżentelmenów - Whitfield Diffie oraz Martin Hellman - postanowiło (w pracy New Directions in Cryptography) bezczelnie zapytać: a może jednak się da? Więcej, już rok później panowie Ron Rivest, Adi Shamir oraz Leonard Adleman (korzystając ze wskazówek z pracy D-H) wykazali, że faktycznie: da się! Czytelnik Logiczny powinien w tym momencie poczuć co najmniej niesmak. Akapit wyżej pokazaliśmy dowód, że czegoś się nie da, a dalej coś tam jeszcze dywagujemy? Haczyk - jak zwykle w matematyce - tkwi w założeniach. Diffie i Hellman nie wykazali, że powyższy dowód jest błędny. Zaproponowali tylko pewne dodatkowe założenie, przy którym ten dowód przestaje być poprawny! Konkretnie chodzi o punkt 5. tego dowodu. Jeśli założymy (jak proponują D-H), że Helga ma ograniczoną moc obliczeniową, to wcale nie jest jasne, że będzie potrafiła szybko odwrócić znaną sobie funkcję  Tym tropem poszli Rivest, Shamir i Adleman, proponując swój szyfr, znany dziś jako szyfrowanie RSA.
Tym tropem poszli Rivest, Shamir i Adleman, proponując swój szyfr, znany dziś jako szyfrowanie RSA.
Zanim przejdziemy do szczegółów, spróbujmy naświetlić samą esencję pomysłu. Idea opiera się na spostrzeżeniu, że (generalnie) mnożenie jest szybkie, ale już jego odwracanie (czyli rozkład na czynniki pierwsze) - bardzo trudne. Innymi słowy, chodzi o znalezienie takich funkcji 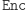 oraz
oraz 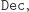 aby do wyliczania
aby do wyliczania 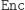 wystarczała znajomość
wystarczała znajomość 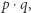 ale już do szybkiego obliczania
ale już do szybkiego obliczania 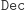 - konieczne były zarówno
- konieczne były zarówno 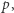 jak i
jak i 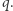 Wówczas Bogumił może wszystkim (i Aldonie, i Heldze, i Kamili, i Markowi, i Szymonowi i każdemu, kto tylko będzie chciał) bez skrępowania ujawniać opis
Wówczas Bogumił może wszystkim (i Aldonie, i Heldze, i Kamili, i Markowi, i Szymonowi i każdemu, kto tylko będzie chciał) bez skrępowania ujawniać opis 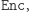 ALE zachowując dla siebie czynniki
ALE zachowując dla siebie czynniki 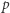 oraz
oraz 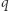 (czyli w istocie opis
(czyli w istocie opis 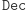 ). Naprawdę jest to troszkę bardziej skomplikowane i wygląda tak.
). Naprawdę jest to troszkę bardziej skomplikowane i wygląda tak.
Rzeczywiście Bogumił wybiera dwie duże (rzędu setek cyfr) liczby pierwsze 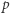 i
i 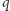 oraz oblicza ich iloczyn
oraz oblicza ich iloczyn 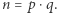 Następnie oblicza
Następnie oblicza 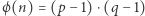 oraz losuje dowolną liczbę
oraz losuje dowolną liczbę  względnie pierwszą z
względnie pierwszą z 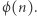 Teraz znajduje taką liczbę
Teraz znajduje taką liczbę 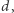 że
że
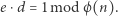 |
(*) |
Okazuje się, że powyższa operacja (wyznaczenie 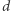 ) da się wykonać bardzo szybko (np. za pomocą rozszerzonego algorytmu Euklidesa), gdy znamy
) da się wykonać bardzo szybko (np. za pomocą rozszerzonego algorytmu Euklidesa), gdy znamy 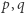 oraz
oraz 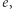 natomiast wierzymy, że jest bardzo trudna, gdy znamy tylko
natomiast wierzymy, że jest bardzo trudna, gdy znamy tylko 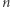 oraz
oraz 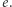 Pozostaje opisać funkcję szyfrującą i deszyfrującą
Pozostaje opisać funkcję szyfrującą i deszyfrującą 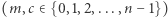 :
:

Aby uznać szyfrowanie RSA za poprawne i bezpieczne, należy sprawdzić, że:
- (a)
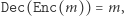 czyli, że
czyli, że 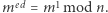 Dowód tego faktu pominiemy, pozostawiając tylko uwagę, że - korzystając z kilku faktów z teorii liczb - da się go wyprowadzić wprost z równania (*).
Dowód tego faktu pominiemy, pozostawiając tylko uwagę, że - korzystając z kilku faktów z teorii liczb - da się go wyprowadzić wprost z równania (*).- (b)
- Znajomość opisu
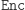 (czyli liczb
(czyli liczb 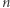 i
i  ) nie pomoże odtworzyć funkcji
) nie pomoże odtworzyć funkcji 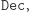 gdyż - jak już wspomnieliśmy - wierzymy, że z
gdyż - jak już wspomnieliśmy - wierzymy, że z  i
i  nie da się łatwo obliczyć
nie da się łatwo obliczyć 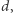 które jest niezbędnym elementem opisu
które jest niezbędnym elementem opisu 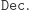
Jak to wygląda w praktyce?
Szyfrowanie RSA jest niezwykle popularne i wygodne. Aby z niego korzystać, należy postąpić dokładnie tak, jak Bogumił w opisie wyżej. Następnie parę 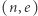 (tak zwany klucz publiczny) należy rozgłaszać wszem i wobec, ponieważ jej znajomość umożliwia światu bezpieczne wysyłanie komunikatów przeznaczonych tylko dla nas. Z drugiej strony - liczbę
(tak zwany klucz publiczny) należy rozgłaszać wszem i wobec, ponieważ jej znajomość umożliwia światu bezpieczne wysyłanie komunikatów przeznaczonych tylko dla nas. Z drugiej strony - liczbę 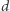 (osobisty klucz prywatny) oraz rozkład
(osobisty klucz prywatny) oraz rozkład 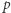 i
i 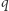 należy trzymać w wielkiej tajemnicy i nigdy nikomu nie zdradzać.
należy trzymać w wielkiej tajemnicy i nigdy nikomu nie zdradzać.
Jaki to ma związek z podpisem cyfrowym?
Podpis cyfrowy Bogumiła to taka para funkcji 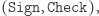 że:
że:
- tylko Bogumił potrafi obliczać wartości
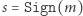 (czyli podpisywać
(czyli podpisywać 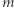 );
); - każdy potrafi obliczać wartości
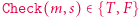 (czyli sprawdzać autentyczność podpisu
(czyli sprawdzać autentyczność podpisu  pod dokumentem
pod dokumentem 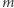 );
); - funkcja
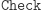 zachowuje się dobrze, to znaczy
zachowuje się dobrze, to znaczy 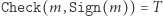 oraz
oraz 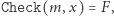 jeśli tylko
jeśli tylko 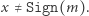
Powyższa definicja wydaje się zupełnie intuicyjna i nie wymaga szerszego komentarza. Wyzwaniem jest jednak znaleźć odpowiednie 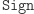 oraz
oraz 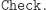 Okazuje się, że znajomość RSA bardzo nam pomoże. Przyjmijmy bowiem:
Okazuje się, że znajomość RSA bardzo nam pomoże. Przyjmijmy bowiem:

gdzie 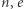 oraz
oraz 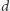 są takie same jak w RSA (w szczególności:
są takie same jak w RSA (w szczególności: 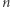 i
i  są publiczne, a
są publiczne, a 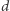 - znane tylko Bogumiłowi).
- znane tylko Bogumiłowi).
Innymi słowy: podpis 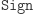 zachowuje się jak
zachowuje się jak 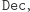 a weryfikacja podpisu
a weryfikacja podpisu  dokumentu
dokumentu 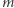 sprowadza się do sprawdzenia, czy
sprowadza się do sprawdzenia, czy 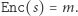
Teraz widać, że bezpieczeństwo takiego podpisu jest takie samo, jak bezpieczeństwo RSA. Jeśli bowiem (w RSA) tylko Bogumił mógł deszyfrować, to u nas tylko on może podpisywać. Skoro wcześniej każdy mógł szyfrować ( 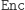 jest publiczna), to teraz każdy może obliczać funkcję
jest publiczna), to teraz każdy może obliczać funkcję 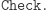 Wreszcie - funkcja
Wreszcie - funkcja 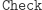 zachowuje się zgodnie z oczekiwaniami, co wynika wprost z faktu, że
zachowuje się zgodnie z oczekiwaniami, co wynika wprost z faktu, że 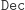 jest odwrotna do
jest odwrotna do 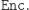
Postscriptum
Na zakończenie jeszcze mała obserwacja, która na razie pewnie wyda się mało użyteczna (choć zaryzykujemy stwierdzenie, że jest elegancka i zaskakująca), ale będziemy jej potrzebować w kolejnych częściach cyklu A jednak się da. Otóż chcemy zdefiniować protokół tak zwanego ślepego podpisu. To znaczy: chcielibyśmy, aby Bogumił mógł (jeśli tylko ma taką fantazję) pozwolić Aldonie na podpisanie czegoś, czego sam nigdy nie zobaczy na oczy. Możemy zrobić to tak:
- 1.
- Aldona wybiera dokument do podpisu
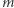 oraz losową liczbę
oraz losową liczbę 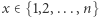 ;
; - 2.
- Aldona wysyła do Bogumiła liczbę
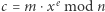 ;
; - 3.
- Bogumił oblicza
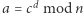 i odsyła wynik Aldonie;
i odsyła wynik Aldonie; - 4.
- Aldona oblicza
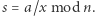
Jako ćwiczenie pozostawiamy sprawdzenie, że w protokole powyżej: (1) Bogumił nie jest w stanie odtworzyć dokumentu 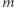 oraz (2) liczba
oraz (2) liczba  jest poprawnym podpisem Bogumiła pod dokumentem
jest poprawnym podpisem Bogumiła pod dokumentem 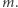
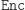 musi być szybkie, żeby szyfrowanie było efektywne.
musi być szybkie, żeby szyfrowanie było efektywne.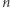 na czynniki.
na czynniki.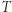 to true, a
to true, a 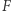 to false.
to false.