Najskuteczniejszym (i najprostszym) sposobem szyfrowania jest one time pad, w którym tajny agent (nadamy mu kryptonim 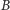) ustala z odbiorcą swoich wiadomości (nazywanym dalej admirałem 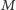) klucz 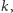będący pewnym zerojedynkowym ciągiem. Kiedy 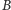chce przesłać 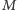uzyskane sekrety, najpierw konwertuje je w ustalony sposób na zerojedynkowy ciąg 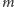(np. 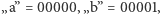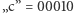itd.), a następnie wysyła ciąg (zwany kryptogramem), który na 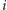-tej współrzędnej ma resztę z dzielenia przez 2 sumy 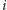-tych współrzędnych ciągów 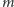i 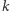(operacja ta w informatycznej nowomowie nazywana jest xorem ciągów 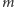i 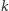i oznaczana przez 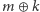). W ten sposób, jeśli tajna informacja to 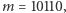a 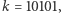to kryptogramem jest 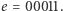Aby odcyfrować otrzymany kryptogram, 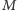wykonuje tę samą operację, która posłużyła 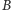do szyfrowania - oblicza 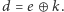Nietrudno sprawdzić, że 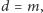mamy bowiem 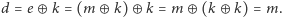Ponadto, jeśli zostanie przechwycone przez wrogie siły (reprezentowane przez nikczemnego doktora 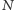), to nie będą one w stanie wywnioskować stąd 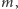gdyż byłoby to równoważne z ustaleniem wartości klucza 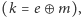o którym zakładamy przecież, że jest znany tylko 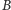i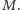

Słabym punktem powyższej procedury jest konieczność spotkania się 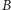i 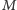w celu ustalenia klucza, nie mogą go bowiem przesłać na odległość, gdyż mógłby on zostać "podsłuchany" przez doktora 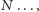a może jednak mogą?

W 1976 roku Whitfield Diffie i Martin Hellman zaproponowali protokół (znany teraz pod nazwiskami twórców), który pozwala na ustalenie klucza w taki sposób, że nawet jeśli komunikacja zostanie podsłuchana, to strona podsłuchująca nie będzie w stanie odcyfrować prawdziwej wartości klucza. Protokół ten wiąże się z trudnością wykonania tzw. logarytmu dyskretnego, czyli odpowiedzi na pytanie w rodzaju "do jakiej potęgi należy podnieść 123, aby otrzymać resztę 321 z dzielenia przez 983?". Jak jednak można dowiedzieć się w tym numerze, w "postkwantowym" świecie z dostępem do wydajnych komputerów kwantowych logarytm dyskretny przestaje być zadaniem trudnym. Na szczęście (dla agenta 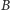) komputery kwantowe dostarczają również nowe narzędzia do kodowania wiadomości i to takie, których w "dowodliwy" sposób same nie mogą przełamać. W tym kontekście podstawową własnością komputerów kwantowych jest fakt, że sprawdzenie stanu ich pamięci często powoduje zmianę tego stanu, co pozwala na wykrycie próby podsłuchania informacji i zerwanie połączenia, a potem poszukiwanie bezpieczniejszego kanału komunikacji. Realizacja tej idei została opisana w 1984 roku przez Charlesa Bennetta i Gillesa Brassarda, a przedstawiony przez nich protokół to tytułowy BB84.

Aby wytłumaczyć działanie BB84, zanurzymy się w oparach absurdu i będziemy wyobrażać sobie najprostszy, jednokubitowy komputer kwantowy jako czarną skrzynkę, w której zamknięta jest tarcza zegara wraz ze wskazówką godzinową - godzinę przez nią wskazywaną nazwiemy stanem komputera. W jaki sposób można czegoś się o nim dowiedzieć? Można poprosić komputer o porównanie swojego stanu z konkretną "eLką" - pod tym pojęciem rozumieć będziemy układ dwóch "prostopadłych" godzin, np. 1:30 i 4:30, a ogólnie godzinę 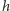wraz z godziną 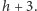Jeśli poprosimy komputer znajdujący się w stanie 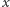o porównanie z eLką 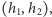to możemy otrzymać dwie odpowiedzi: 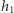z prawdopodobieństwem 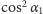oraz 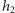z prawdopodobieństwem 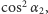gdzie 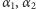to kąty, jakie tworzy godzina odpowiednio z godzinam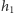i i 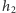(prawdopodobieństwa te sumują się do 1, dlaczego?). Ponadto po przedstawieniu odpowiedzi komputer nagina do niej rzeczywistość, to znaczy zmienia swój stan na zgodny z odpowiedzią.

Dla przykładu, jeśli komputer był w stanie 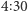i poprosiliśmy go o porównanie z eLką 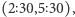to z prawdopodobieństwem 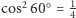otrzymamy odpowiedź 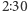(i wówczas stan komputera zmieni się na 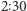), a z prawdopodobieństwem 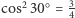usłyszymy 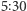i taką godzinę zacznie wskazywać wskazówka wewnątrz czarnej skrzynki. Zwróćmy ponadto uwagę, że jeśli stan komputera pokrywa się z jedną z godzin z wybranej przez nas eLki, to na pewno uzyskamy tę godzinę w odpowiedzi, a stan komputera nie ulegnie zmianie. Przejdźmy do opisu protokołu. 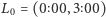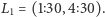Wyróżnijmy na początku dwa rodzaje eLek: i Agent 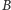zaopatruje się w 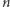jednokubitowych komputerów kwantowych (gdzie jest raczej duże) i wybiera losowo dwa ciągi zerojedynkowe: 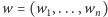oraz 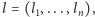a następnie stan 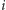-tego komputera ustawia na godzinę 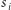będącą 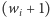-szą współrzędną eLki 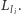W ten sposób, jeśli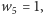 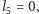to stan piątego komputera zostanie ustawiony na drugą współrzędną 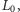czyli na 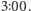Następnie agent 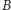przesyła pocztą wszystkie komputery do 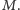Ten ostatni również ustala zerojedynkowy ciąg 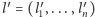i odczytuje stan 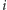-tego komputera przy użyciu eLki 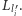Później na swojej stronie internetowej (lub innym ogólnodostępnym medium, które tylko on może edytować) udostępnia użyty ciąg 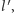w odpowiedzi na co agent 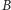publikuje na swojej stronie ciąg 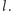Zauważmy, że wszędzie tam, gdzie 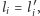admirał 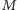odczytał godzinę zakodowaną przez agenta 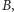a skoro wie również, jaka eLka posłużyła do jej zakodowania, pozna 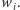Zwróćmy ponadto uwagę, że szansa na to, by 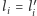wynosi 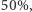dlatego 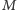powinien poznać około połowy wyrazów ciągu 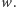Na koniec 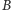upublicznia połowę z tych wyrazów 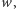które powinien był poznać 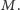Dlaczego?

Przypomnijmy, że cały ten ambaras miał na celu popsucie szyków nikczemnemu doktorowi 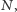który przechwycił paczkę z komputerami i postanowił odczytać ich stany. Poprzez odczyt stanu 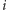-tego komputera stwarza on szansę na zmianę tego stanu i tylko w tej sytuacji możliwe jest, aby 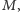pomimo równości 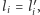odczytał złą wartość 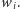Rozpatrzmy sytuację, w której doktor 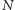użył 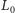do odczytania stanu 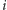-tego komputera, przy czym 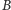i 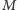użyli na tej współrzędnej identyczne eLki (a zatem, gdyby nie podsłuch, 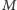na pewno poznałby wartość 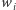). Jeśli 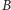również zakodował wiadomość przy użyciu eLki 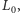to 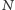odczytał pierwotny stan 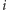-tego komputera (w związku z czym również 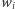) i go nie zmienił, w związku z czym szpiegostwo pozostanie niewykryte. 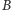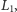Jeśli jednak użył to 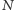zmienił stan komputera na którąś z godzin 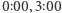i w każdym z tych przypadków 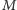będzie miał szansę 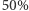na błędny odczyt 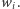Podsumowując, jeśli doktor 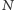wybrał eLkę 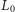do odczytu stanu 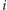-tego komputera, to z prawdopodobieństwem 25% admirał 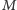odczyta złą wartość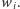

Okazuje się, że jest tak niezależnie od eLki wybranej przez doktora 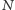(uzasadnienie jest wdzięcznym ćwiczeniem z trygonometrii). Fakt ten tłumaczy ostatnią, "kontrolną" fazę naszego protokołu: jeśli po ujawnieniu przez agenta 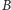połowy wyrazów ciągu 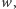dla których 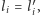admirał 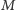stwierdzi jakąkolwiek niezgodność ze swoimi odczytami, oznaczać to będzie, że komunikacja została podsłuchana i w związku z tym należy ją powtórzyć, najlepiej przy użyciu bardziej wiarygodnej poczty. Jeśli natomiast wszystkie wartości ujawnione przez 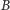zgadzały się z odczytami 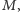to prawdopodobieństwo takiego zdarzenia przy założeniu o podsłuchiwaniu kanału wyniosłoby 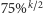(gdzie 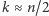to liczba indeksów 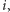dla których 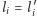), co dla odpowiednio dużych wartości jest na tyle małe, że można z czystym sumieniem odrzucić hipotezę o podsłuchu i wykorzystać nieujawnione przez agenta 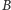i poprawnie obliczone przez 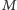wartości 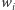jako wspólny klucz.

Najwyższy czas opuścić opary absurdu i stawić czoła brutalnej, szpiegowskiej rzeczywistości - przecież żaden tajny agent nie będzie wysyłał pocztą tysiąca jednokubitowych komputerów kwantowych. Pocztą pewnie nie, ale już światłowodem bez problemu! Okazuje się bowiem (za czym stoi fizyczna magia, o której trochę piszemy w tym numerze), że jednokubitowy komputer kwantowy, ta czarna skrzynka z zamkniętym w środku zegarem, to (w rozsądnym uproszczeniu) po prostu foton, a tych przecież nie brakuje i przesyłać przy użyciu światłowodu też je można. Nie jest to jednak tanie - agenci chcący zaopatrzyć się w parę odbiorników oraz odpowiedni światłowód muszą liczyć się z wydatkiem rzędu 100 tysięcy dolarów; czego jednak się nie robi w tajnej służbie Jej Królewskiej Mości...

---