Rys. 1 Płaszczyzna dziewięciu punktów

Przyjmijmy, że owe dziewięć punktów tworzy całą "płaszczyznę", którą będziemy dysponować. Ułóżmy je w kształt kwadratu i nadajmy punktom współrzędne jak na rysunku 1

Jak na każdej płaszczyźnie, także na tej możemy wyróżnić pewne figury.

Zacznijmy od najprostszej figury - prostej. Ustalmy, że zbiór punktów płaszczyzny tworzy prostą, jeżeli wszystkie punkty mają dokładnie jedną taką samą współrzędną (znajdują się w linii pionowej lub poziomej) albo jeżeli każde dwa punkty z tego zbioru różnią się dwiema współrzędnymi. Zauważmy, że każda prosta na dobrze nam znanej płaszczyźnie również spełnia ten warunek, jednak nie każdy zbiór spełniający ten warunek tworzy prostą. Ile punktów zawiera zdefiniowana przed momentem figura? Otóż, powyższy warunek mogą spełniać zbiory zawierające dwa lub trzy punkty. Każda prosta powinna jednak mieć tyle samo punktów - wobec tego do opisu prostej w geometrii dziewięciu punktów należy dodać, że musi zawierać dokładnie trzy punkty. To ile jest tych prostych?

Do konstrukcji bardziej zaawansowanych figur przydatna będzie odległość, ale zupełnie inna niż ta, o której informuje nas linijka, bo i płaszczyzna jest nieco inna. Odległość między dwoma punktami zdefiniujmy jako liczbę współrzędnych, którymi te punkty się różnią. Czyli odległość między punktami 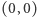oraz 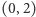wynosi 1, między 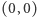i 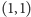wynosi 2. Tak uzbrojeni możemy skonstruować trójkąt równoboczny (taki zupełnie "normalny", znaczy figurę o trzech wierzchołkach, w której odległość między każdymi dwoma wierzchołkami jest taka sama). I niespodzianka: na jednej prostej leżą trzy punkty, których odległości są parami równe. Na płaszczyźnie dziewięciu punktów możemy zatem mówić o "trójkącie równobocznym", którego wierzchołki są współliniowe.

Trójkąty równoramienne mają dwa "boki" równej długości, więc, gdy trójkąt nie jest równoboczny, długości boków mogą wynosić tylko 2, 2, 1 lub 1, 1, 2. Drogi Czytelniku, zechciej pobawić się w konstrukcję takich trójkątów. A co byś powiedział na trójkąty różnoboczne?

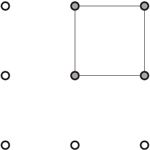
Rys. 2 Romb, ale czy na pewno kwadrat?

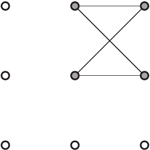
Rys. 3 Równoległobok niebędący rombem

Przejdźmy do figur o większej liczbie wierzchołków. Romb, jak wiadomo, ma cztery "boki" jednakowej długości (możliwości to 1 lub 2), jego konstrukcja nie powinna przysparzać problemów. Choć po dłuższym (lub krótszym) zastanowieniu… może obudzić się pewna wątpliwość. Spójrzmy na rysunek 2, pomocnicza linia łączy sąsiadujące ze sobą wierzchołki czworokąta. Każdy "bok" ma długość 1, figura jest więc rombem, ale te same cztery wierzchołki mogą sąsiadować ze sobą w inny sposób (Rys. 3). Drugi czworokąt ma boki parami równe 2 i 1, zdaje się być równoległobokiem; zauważmy, że skrzyżowane na rysunku odcinki nie przecinają się! Na standardowej płaszczyźnie cztery wierzchołki również nie muszą jednoznacznie wyznaczać czworokąta. Czy wiesz, jakich czworokątów dotyczy ta niejednoznaczność?

Kolejnym wyzwaniem jest zdefiniowanie kwadratu. Chcemy skonstruować romb, którego wszystkie kąty mają 90 stopni. Musimy więc zdecydować, jak na naszej dziewięciopunktowej płaszczyźnie określić prostopadłość. W podręcznikach do "prawdziwej" geometrii można znaleźć wzór mówiący, że odcinek o końcach 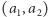i 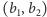jest prostopadły do odcinka o końcach 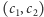i 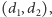gdy zachodzi równość

Gdy zastosujemy ten przepis do naszej geometrii, okaże się, że i u nas daje to prawdziwą prostopadłość. Ile zatem kwadratów istnieje na naszej płaszczyźnie?

Drogi Czytelniku, konstruuj okręgi, trapezy, deltoidy, prostokąty, czy inne figury, na które przyjdzie Ci ochota. Można próbować znaleźć wszystkie dziewięciokąty. Można szukać kolejnych odpowiedników znanych nam obiektów geometrycznych lub badać, czy i na ile zachodzą w tej geometrii znane twierdzenia. Nic nie stoi na przeszkodzie, aby zwiększyć liczbę punktów płaszczyzny tak, aby przedstawienie dwunastokątów i innych figur stało się możliwe. Do dzieła.