W rozumowaniach był błąd
W poprzednim numerze Delty przedstawiłem trzy dowody V postulatu Euklidesa. Dla wszystkich Czytelników było jasne, że zawierają one błędy. Fakt, że mimo to każdy z nich przez pewien czas był uznany za poprawny, wskazuje na ogromny kłopot, jakim dla myślicieli – już niekoniecznie matematyków – było przyjęcie do wiadomości, że mogą istnieć dwie wykluczające się, ale poprawne, a więc w szczególności niesprzeczne teorie opisujące ten sam obiekt, w tym przypadku przestrzeń. A przecież przestrzeń, w której „odbywa się” Wszechświat, jest jedna.
Powstało więc pytanie, jak – niezależnie od odwoływania się do Natury – można stwierdzić poprawność teorii. Rozwiązanie przyniosła lekka modyfikacja tego pytania przez Felixa Kleina: zapytał on
jak stwierdzić, że jedna teoria jest co najmniej tak poprawna, jak druga?
I odpowiedział na to pytanie: jeśli w teorii
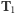 można zbudować
model teorii
można zbudować
model teorii
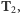 to teoria
to teoria
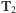 jest co najmniej tak samo poprawna,
jak teoria
jest co najmniej tak samo poprawna,
jak teoria
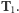
Po czym zbudował (w 1870 roku) model geometrii powstającej przez dołączenie do czterech początkowych postulatów Euklidesa zaprzeczenia piątego postulatu w geometrii euklidesowej (model Kleina) oraz w tej geometrii model geometrii euklidesowej (horysfera). W ten sposób wykazał, że obie geometrie są jednakowo poprawne.
A filozoficzny problem istnienia dwu teorii opisujących ten sam obiekt został niewiele później rozstrzygnięty według pomysłu fizyka, Hermanna Helmholtza, który w pracy O faktach, które leżą u podstaw geometrii zaproponował, by matematyki nie uważać za naukę przyrodniczą, lecz za skrzynkę z narzędziami do uprawiania nauk przyrodniczych.
Model Kleina
Do wskazania błędów w przytoczonych dowodach V postulatu potrzebny będzie nam – rzecz jasna – tylko pierwszy z modeli zbudowanych przez Kleina. Oto on.
- Płaszczyzną będzie wnętrze koła (bez brzegu! – oznaczmy ten brzeg
 ).
).
- Prostymi będą cięciwy tego koła (oczywiście, bez końców).
- Proste będą prostopadłe wtedy i tylko wtedy, gdy przedłużenie
jednej z nich przechodzi przez punkt przecięcia stycznych do
 w końcach drugiej (okazuje się, że jest to relacja
symetryczna) lub gdy jedna z nich przechodzi przez środek koła,
a druga jest euklidesowo do niej prostopadła.
w końcach drugiej (okazuje się, że jest to relacja
symetryczna) lub gdy jedna z nich przechodzi przez środek koła,
a druga jest euklidesowo do niej prostopadła.
To określa model całkowicie, a wynika z tego, między innymi, że
- odległość punktów
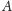 i
i
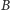 to
to
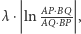
gdzie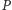 i
i
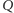 to
końce prostej
to
końce prostej
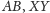 to euklidesowa długość odcinka
to euklidesowa długość odcinka
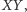 a
a
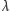 jest dowolnie ustaloną stałą dodatnią;
jest dowolnie ustaloną stałą dodatnią;
- punkty równoodległe od prostej tworzą elipsę styczną do
 w końcach tej prostej;
w końcach tej prostej;
- kąt między prostymi to euklidesowy kąt, jaki tworzą
okręgi prostopadłe do
 i przechodzące przez końce tych
prostych.
i przechodzące przez końce tych
prostych.
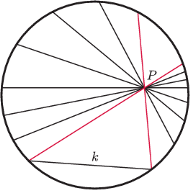
Rys. 1
Czytelnik Ciekawski może z tego wyprowadzić wszelkie własności tej
nieeuklidesowej geometrii zwanej geometrią Bolyaia–Łobaczewskiego na cześć
dwóch odważnych matematyków, którzy pierwsi uparli się, że taka
geometria istnieje (lub geometrią hiperboliczną ze względu na jej analityczne
własności). My zauważymy wstępnie, że nie jest w niej spełniony V postulat:
przez punkt
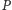 poza prostą
poza prostą
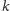 przechodzi nieskończenie
wiele prostych z nią rozłącznych (Rys. 1). O tych dwu, które mają z
przechodzi nieskończenie
wiele prostych z nią rozłącznych (Rys. 1). O tych dwu, które mają z
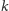 wspólne końce, mówimy, że są do
wspólne końce, mówimy, że są do
 równoległe,
o pozostałych – że są nadrównoległe.
równoległe,
o pozostałych – że są nadrównoległe.
Na czym polegały błędy?
Już z oglądu rysunku 1 można stwierdzić, że Saccheri żadnego błędu matematycznego nie popełnił – w geometrii Bolyaia–Łobaczewskiego (B–Ł) proste równoległe są asymptotyczne. Mylił się tylko w intuicji, że takie coś prostym przydarzyć się nie może. Faktycznie jego praca Euclides ab omni naevo vindicatus była pierwszą pracą z geometrii B–Ł, ale o tym przekonano się dopiero dwa wieki później.
Rys. 2
Legendre popełnił – można powiedzieć – pół błędu: pierwsza część jego
dowodu, gdy wykazuje, że suma kątów trójkąta w geometrii absolutnej nie
może być większa od
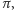 jest poprawna. Uzyskany wynik dziś nazywa
się twierdzeniem Saccheriego–Legendre’a, bo i u Saccheriego można znaleźć
podobne rozumowanie.
jest poprawna. Uzyskany wynik dziś nazywa
się twierdzeniem Saccheriego–Legendre’a, bo i u Saccheriego można znaleźć
podobne rozumowanie.
Natomiast dowód, że nie ma trójkątów o sumie kątów mniejszej od
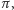 korzysta ze zdawałoby się oczywistej przesłanki: przez punkt
wewnątrz kąta wypukłego można poprowadzić prostą przecinającą oba jego
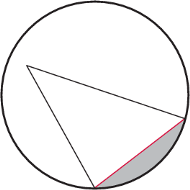
ramiona. Jej fałszywość widać na rysunku 2 Kolorowa prosta jest
równoległa do obu ramion kąta – nazywa się ją prostą zagradzającą.
Zacieniowany obszar za nią składa się – co łatwo sprawdzić linijką –
z punktów, przez które nie można poprowadzić prostej przecinającej oba
ramiona kąta (punkty
korzysta ze zdawałoby się oczywistej przesłanki: przez punkt
wewnątrz kąta wypukłego można poprowadzić prostą przecinającą oba jego
ramiona. Jej fałszywość widać na rysunku 2 Kolorowa prosta jest
równoległa do obu ramion kąta – nazywa się ją prostą zagradzającą.
Zacieniowany obszar za nią składa się – co łatwo sprawdzić linijką –
z punktów, przez które nie można poprowadzić prostej przecinającej oba
ramiona kąta (punkty
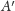 i
i
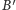 z dowodu Legendre’a mogą nie
istnieć).
z dowodu Legendre’a mogą nie
istnieć).
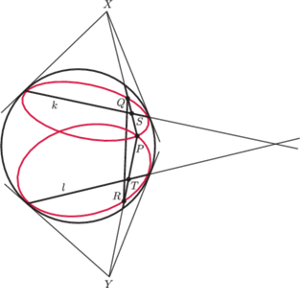
Rys. 3
Sprawa z dowodem Farkasa Bolyaia jest (chyba) prostsza, choć obrazek będzie większy. Okazuje się bowiem, że w geometrii B–Ł istnieją trójkąty, na których nie można opisać okręgu – po prostu symetralne ich boków nie przecinają się! Pokazuje to rysunek 3
Nieprzecinające się proste
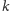 i
i
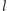 będą symetralnymi trójkąta,
który buduje się tak. Bierzemy między nimi jakiś punkt
będą symetralnymi trójkąta,
który buduje się tak. Bierzemy między nimi jakiś punkt
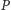 i rysujemy
elipsy przechodzące przez ten punkt i styczne do
i rysujemy
elipsy przechodzące przez ten punkt i styczne do
 odpowiednio
w końcach prostych
odpowiednio
w końcach prostych
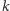 i
i
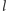 – są to linie, które składają się
z punktów odległych tak jak
– są to linie, które składają się
z punktów odległych tak jak
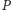 odpowiednio od prostej
odpowiednio od prostej
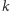 i
i
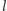 (druga czarna kropka na poprzedniej stronie) – zatem
(druga czarna kropka na poprzedniej stronie) – zatem
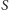 jest
środkiem
jest
środkiem
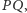 a
a
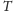 środkiem
środkiem
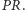 Każda prosta, której
przedłużenie przechodzi przez
Każda prosta, której
przedłużenie przechodzi przez
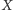 (przez
(przez
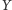 ), jest prostopadła do
), jest prostopadła do
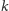 (do
(do
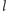 ) – trzecia kolorowa kropka. Zatem
) – trzecia kolorowa kropka. Zatem
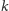 jest symetralną
jest symetralną
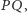 a
a
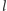 symetralną
symetralną
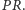 Wobec tego na trójkącie
Wobec tego na trójkącie
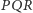 nie można opisać okręgu.
nie można opisać okręgu.
Inne zdania równoważne V postulatowi
Zatem każde ze zdań
- przez punkt wewnętrzny kąta wypukłego można poprowadzić prostą przecinającą oba ramiona kąta;
- na trójkącie można opisać okrąg;
jest równoważne V postulatowi na gruncie początkowych czterech.
Czytelnik Zainteresowany sprawdzi, że podobnie jest ze zdaniami:
- istnieją nieprzystające trójkąty podobne;
- na płaszczyźnie każda prosta przecina przynajmniej jedną z przecinających się prostych;
- istnieją trzy współliniowe punkty jednakowo odległe od danej prostej;
- odległość punktów zorientowanej prostej od innej prostej jest funkcją monotoniczną;
- odległość punktów prostej od współpłaszczyznowej i rozłącznej z nią prostej jest ograniczonado wyboru: z góry lub z dołu);
- istnieje prostokąt;
- wysokości trójkąta przecinają się
itd.