Bańka jaka jest, każdy widzi

Każdy widział kiedyś bańki mydlane. Nie ma co ukrywać, są one okrągłe. Tylko dlaczego?
Nie wiadomo, czemu to pytanie miałoby służyć, ale zastanówmy się chwilę. Czy gdyby się postarać, to czy można wydmuchać bańkę-torus, czyli bańkę w kształcie dętki rowerowej? A jeśli już bańka musi mieć kształt sfery, to czy może być to sfera zdeformowana, na przykład zwężona w talii? Doświadczenie mówi, że nie - o ile bańka nie jest za ciężka, to już chwilę po wydmuchaniu przybiera kształt idealnie okrągłej sfery. Zobaczmy więc, jaka matematyka (i oczywiście fizyka) za tym stoi.
Przy dmuchaniu bańki wtłaczamy do niej powietrze o ciśnieniu wyższym niż atmosferyczne. Równanie Younga-Laplace'a stwierdza, że w dowolnym punkcie 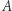 powierzchni bańki zachodzi wzór
powierzchni bańki zachodzi wzór

gdzie 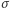 jest napięciem powierzchniowym (współczynnikiem zależnym od parametrów materiału; w przypadku baniek mydlanych możemy przyjąć, że jest ono stałe na całej powierzchni),
jest napięciem powierzchniowym (współczynnikiem zależnym od parametrów materiału; w przypadku baniek mydlanych możemy przyjąć, że jest ono stałe na całej powierzchni), 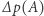 oznacza różnicę ciśnień po obu stronach bańki w punkcie
oznacza różnicę ciśnień po obu stronach bańki w punkcie  a
a 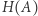 oznacza średnią krzywiznę powierzchni w tym punkcie. Zgodnie ze znanym ze szkoły prawem Pascala, ciśnienie jest stałe na zewnątrz bańki i stałe w jej wnętrzu, a więc różnica
oznacza średnią krzywiznę powierzchni w tym punkcie. Zgodnie ze znanym ze szkoły prawem Pascala, ciśnienie jest stałe na zewnątrz bańki i stałe w jej wnętrzu, a więc różnica 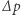 tak naprawdę nie zależy od wyboru punktu. To samo tyczy się zatem średniej krzywizny.
tak naprawdę nie zależy od wyboru punktu. To samo tyczy się zatem średniej krzywizny.
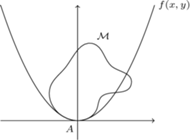
Rys. 1
Pozostaje wyjaśnić, czym ta średnia krzywizna jest. Żeby ją określić, potrzebujemy oprzeć naszą powierzchnię  na płaszczyźnie
na płaszczyźnie 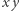 tak, by jej punkt
tak, by jej punkt 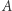 dotykał początku układu współrzędnych (Rys. 1). Następnie wybieramy funkcję kwadratową dwóch zmiennych, czyli funkcję postaci
dotykał początku układu współrzędnych (Rys. 1). Następnie wybieramy funkcję kwadratową dwóch zmiennych, czyli funkcję postaci 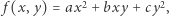 której wykres najlepiej przybliża
której wykres najlepiej przybliża 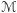 w otoczeniu
w otoczeniu 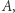 i definiujemy średnią krzywiznę jako
i definiujemy średnią krzywiznę jako

Średniej krzywizny nie należy mylić z krzywizną Gaussa, którą definiuje się w podobny sposób jako 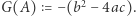
Nazwa średnia bierze się stąd, że gdybyśmy przecięli 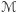 jakąś płaszczyzną zawierającą oś
jakąś płaszczyzną zawierającą oś  i dla powstałej na przecięciu krzywej obliczyli krzywiznę w punkcie
i dla powstałej na przecięciu krzywej obliczyli krzywiznę w punkcie  to
to 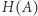 równa się średniej wartości wszystkich uzyskanych w ten sposób pomiarów. Można powiedzieć nieściśle, że im większa krzywizna, tym bardziej powierzchnia zagina się do wewnątrz.
równa się średniej wartości wszystkich uzyskanych w ten sposób pomiarów. Można powiedzieć nieściśle, że im większa krzywizna, tym bardziej powierzchnia zagina się do wewnątrz.
Przykładowo, jeśli sferę o promieniu 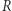 położyć w wyżej opisany sposób, to dolna półsfera jest wykresem funkcji
położyć w wyżej opisany sposób, to dolna półsfera jest wykresem funkcji  W otoczeniu zera najlepiej przybliża ją funkcja kwadratowa
W otoczeniu zera najlepiej przybliża ją funkcja kwadratowa  więc średnia krzywizna wynosi
więc średnia krzywizna wynosi 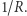 Oczywiście nie ma znaczenia, który punkt obraliśmy jako punkt podparcia, więc sfera ma stałą średnią krzywiznę równą
Oczywiście nie ma znaczenia, który punkt obraliśmy jako punkt podparcia, więc sfera ma stałą średnią krzywiznę równą 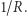
W latach pięćdziesiątych XX wieku Aleksandr Aleksandrow wykazał, że jest to jedyna zamknięta (czyli ograniczona, domknięta i pozbawiona brzegu, który ma na przykład półsfera) powierzchnia o tej własności:
Twierdzenie (Aleksandrow). Jeśli spójna i zamknięta powierzchnia 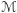 w przestrzeni trójwymiarowej ma taką samą średnią krzywiznę
w przestrzeni trójwymiarowej ma taką samą średnią krzywiznę  w każdym swoim punkcie, to jest sferą o promieniu
w każdym swoim punkcie, to jest sferą o promieniu 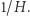
Twierdzenie to wyjaśnia okrągłość baniek. Rzeczywiście, powierzchnia pojedynczej bańki jest ograniczona i spójna, a z praw Pascala i Younga-Laplace'a wynika, że w każdym punkcie ma tę samą średnią krzywiznę. Z twierdzenia Aleksandrowa wnioskujemy więc, że musi być to sfera. Ponieważ powierzchnie o stałej średniej krzywiźnie są interesujące same w sobie, naszkicujemy teraz dowód twierdzenia. Będzie on oparty na następującym fakcie, którego uzasadnienie odłożymy na później.
Lemat 1. Jeśli powierzchnia 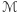 spełnia założenia twierdzenia Aleksandrowa i ma środek ciężkości w punkcie
spełnia założenia twierdzenia Aleksandrowa i ma środek ciężkości w punkcie 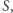 to jest symetryczna względem każdej płaszczyzny przechodzącej przez
to jest symetryczna względem każdej płaszczyzny przechodzącej przez 
Twierdzenie Aleksandrowa jest natychmiastowym wnioskiem z powyższego lematu. Istotnie, weźmy dowolny punkt  różny od
różny od 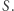 Pokażemy, że
Pokażemy, że 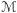 pokrywa się ze sferą
pokrywa się ze sferą 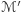 o środku
o środku 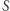 i promieniu
i promieniu  Dla każdego punktu
Dla każdego punktu  można znaleźć płaszczyznę przechodzącą przez
można znaleźć płaszczyznę przechodzącą przez  względem której punkty
względem której punkty  i
i 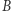 są symetryczne, a więc z symetrii
są symetryczne, a więc z symetrii 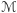 wynika
wynika 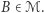 To pokazuje zawieranie
To pokazuje zawieranie 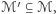 ale skoro
ale skoro 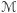 jest spójną powierzchnią, to
jest spójną powierzchnią, to  i
i 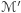 muszą być równe. Jak obliczyliśmy wcześniej, promień musi wynosić
muszą być równe. Jak obliczyliśmy wcześniej, promień musi wynosić 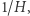 by zgadzała się krzywizna.
by zgadzała się krzywizna.
Naszkicujemy zaraz uzasadnienie Lematu 1, ale najpierw przedstawimy dwa pomocnicze fakty. Rozważmy sytuację, w której dwie powierzchnie  są umieszczone jak
są umieszczone jak 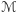 na rysunku 1, przy czym w pewnym otoczeniu początku układu współrzędnych
na rysunku 1, przy czym w pewnym otoczeniu początku układu współrzędnych  powierzchnia
powierzchnia 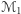 znajduje się nad
znajduje się nad 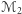 (z możliwymi punktami styku, na przykład w
(z możliwymi punktami styku, na przykład w 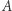 ). Wówczas odpowiadające im funkcje kwadratowe
). Wówczas odpowiadające im funkcje kwadratowe 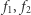 są związane relacją
są związane relacją 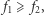 z której w szczególności odczytujemy
z której w szczególności odczytujemy 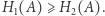 Nierówność ta jest zresztą zgodna z intuicją: "większe zakrzywienie do wewnątrz = większa krzywizna". Uzasadniliśmy w ten sposób
Nierówność ta jest zresztą zgodna z intuicją: "większe zakrzywienie do wewnątrz = większa krzywizna". Uzasadniliśmy w ten sposób
Lemat 2 (Słaba zasada maksimum). Jeśli dane są powierzchnie 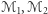 o stałej średniej krzywiźnie
o stałej średniej krzywiźnie  przy czym
przy czym 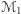 znajduje się nad
znajduje się nad  oraz
oraz 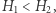 to powierzchnie te nie mogą się stykać w punktach wewnętrznych.
to powierzchnie te nie mogą się stykać w punktach wewnętrznych.
Do dowodu Lematu 1 będzie jednak potrzebna tak zwana silna zasada maksimum, która stwierdza, że również w przypadku 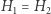 powierzchnie nie mogą się stykać, chyba że są jedną i tą samą powierzchnią; ponadto użyteczny będzie analogiczny wynik w przypadku, gdy punkt styku leży na brzegu obu powierzchni.
powierzchnie nie mogą się stykać, chyba że są jedną i tą samą powierzchnią; ponadto użyteczny będzie analogiczny wynik w przypadku, gdy punkt styku leży na brzegu obu powierzchni.
Lemat 3 (silna zasada maksimum). Dane są dwie różne powierzchnie 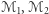 o tej samej stałej średniej krzywiźnie, przy czym
o tej samej stałej średniej krzywiźnie, przy czym 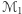 znajduje się nad
znajduje się nad 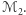 Wówczas:
Wówczas:
- (a)
- powierzchnie te nie mogą się stykać w punktach wewnętrznych,
- (b)
- jeśli
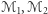 mają brzeg i stykają się w punkcie brzegowym, to nie mogą mieć w tym punkcie tej samej płaszczyzny stycznej.
mają brzeg i stykają się w punkcie brzegowym, to nie mogą mieć w tym punkcie tej samej płaszczyzny stycznej.
Uzasadnienie wymagałoby wprowadzenia narzędzi równań różniczkowych cząstkowych i w związku z tym wykracza poza możliwości niniejszego artykułu. Czytelnik być może zechce uwierzyć mi na słowo, że idea dowodu nie odbiega znacząco od tego, co już zauważyliśmy przy Lemacie 2. Tymczasem przejdziemy do geometrycznej części rozumowania.
Dowód Lematu 1. Zauważmy, że jeśli powierzchnia 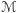 ma jakąś płaszczyznę symetrii, to jej środek ciężkości automatycznie musi leżeć na owej płaszczyźnie. Wystarczy więc, że znajdziemy płaszczyznę symetrii w każdym możliwym kierunku. Dla uproszczenia zapisu skupimy się na szukaniu płaszczyzny symetrii równoległej do płaszczyzny
ma jakąś płaszczyznę symetrii, to jej środek ciężkości automatycznie musi leżeć na owej płaszczyźnie. Wystarczy więc, że znajdziemy płaszczyznę symetrii w każdym możliwym kierunku. Dla uproszczenia zapisu skupimy się na szukaniu płaszczyzny symetrii równoległej do płaszczyzny 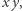 a więc wśród rodziny
a więc wśród rodziny 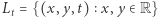 parametryzowanej przez
parametryzowanej przez  Dla każdego innego kierunku dowód wygląda analogicznie.
Dla każdego innego kierunku dowód wygląda analogicznie.
Rys. 2  w dwóch fazach ruchu - tuż przed i tuż po krytycznym momencie
w dwóch fazach ruchu - tuż przed i tuż po krytycznym momencie
Poniższe rozumowanie nosi obecnie nazwę metody ruchomych płaszczyzn, a to dlatego, że będziemy przesuwać płaszczyznę  (poprzez zmianę parametru
(poprzez zmianę parametru 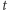 ) tak długo, aż znajdziemy płaszczyznę symetrii.
) tak długo, aż znajdziemy płaszczyznę symetrii.
Wprowadźmy pewne oznaczenia. Dla ustalonego 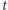 niech
niech  będzie częścią
będzie częścią  znajdującą się odpowiednio nad i pod płaszczyzną
znajdującą się odpowiednio nad i pod płaszczyzną 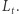 Ponadto część
Ponadto część 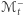 odbitą względem
odbitą względem 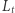 oznaczymy przez
oznaczymy przez 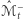 - z nadzieją na równość
- z nadzieją na równość 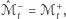 która kończyłaby dowód. Przeanalizujmy, jak ta konfiguracja zależy od
która kończyłaby dowód. Przeanalizujmy, jak ta konfiguracja zależy od 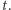 Dla odpowiednio małych wartości
Dla odpowiednio małych wartości 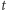 płaszczyzna
płaszczyzna 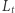 przebiega poniżej
przebiega poniżej 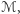 w rezultacie
w rezultacie 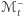 i
i  są puste. Następnie dla pewnego zakresu
są puste. Następnie dla pewnego zakresu 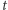 powierzchnia
powierzchnia 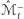 znajduje się pod
znajduje się pod 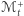 ; od teraz interesować nas będzie największa wartość
; od teraz interesować nas będzie największa wartość 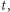 dla której ma to miejsce.
dla której ma to miejsce.
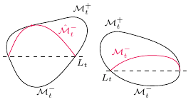
Rys. 3 Dwie możliwości  w krytycznym momencie
w krytycznym momencie
Przypuśćmy, że w tym krytycznym momencie  powierzchnie
powierzchnie  i
i 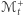 się nie pokrywają. Zauważmy, że mają tę samą stałą średnią krzywiznę
się nie pokrywają. Zauważmy, że mają tę samą stałą średnią krzywiznę 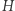 oraz wspólny brzeg, mianowicie przecięcie
oraz wspólny brzeg, mianowicie przecięcie  Ponadto
Ponadto 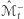 cały czas znajduje się poniżej
cały czas znajduje się poniżej 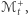 jest to jednak ostatni taki moment - rysunek 3 ilustruje dwie możliwości, jak może on wyglądać (zachęcam Czytelnika do uzasadnienia, że innych możliwości nie ma). W pierwszym przypadku
jest to jednak ostatni taki moment - rysunek 3 ilustruje dwie możliwości, jak może on wyglądać (zachęcam Czytelnika do uzasadnienia, że innych możliwości nie ma). W pierwszym przypadku 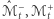 mają wewnętrzny punkt wspólny, co jest wykluczone przez Lemat 3(a); w drugim zachodzi zgodność płaszczyzn stycznych w którymś z punktów brzegowych, co z kolei przeczy Lematowi 3(b).
mają wewnętrzny punkt wspólny, co jest wykluczone przez Lemat 3(a); w drugim zachodzi zgodność płaszczyzn stycznych w którymś z punktów brzegowych, co z kolei przeczy Lematowi 3(b).
Sprzeczność ta pokazuje, że dla tej szczególnej wartości 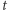 powierzchnie
powierzchnie  i
i 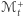 istotnie muszą się pokrywać, a więc
istotnie muszą się pokrywać, a więc 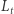 jest szukaną płaszczyzną symetrii
jest szukaną płaszczyzną symetrii  Jak już zauważyliśmy wcześniej, w takim przypadku
Jak już zauważyliśmy wcześniej, w takim przypadku  przechodzi przez środek ciężkości
przechodzi przez środek ciężkości  natomiast wybrany kierunek nie miał znaczenia dla dowodu.
natomiast wybrany kierunek nie miał znaczenia dla dowodu.
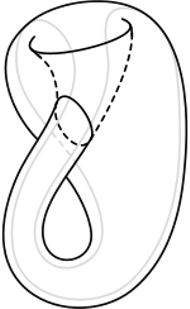
Rys. 4 Immersja butelki Kleina w 
Z ciekawymi problemami w matematyce często jest tak, że ich rozwiązanie stanowi bardziej początek niż koniec historii. Tak było i w tym przypadku - wprowadzona przez Aleksandrowa metoda ruchomych płaszczyzn znalazła zastosowanie w przeróżnych zagadnieniach, niekoniecznie w kontekście powierzchni o stałej średniej krzywiźnie. Natomiast klasyfikacja takich powierzchni jest nadal aktywnie uprawianą dziedziną badań. Jednym z odgałęzień tej dziedziny jest dopuszczenie możliwych samoprzecięć, czyli rozważanie tak zwanych powierzchni immersyjnych (przykładem jest tzw. butelka Kleina).
Rodzina możliwych rozwiązań tego typu okazuje się bogatsza, choć nie jest łatwo się o tym przekonać. Dopiero w 1984 Henry Wente skonstruował różny od sfery "immersyjny przykład" powierzchni o stałej, średniej krzywiźnie - był to torus z samoprzecięciami.
 w dwóch fazach ruchu - tuż przed i tuż po krytycznym momencie
w dwóch fazach ruchu - tuż przed i tuż po krytycznym momencie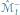 w krytycznym momencie
w krytycznym momencie