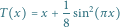Twierdzenie o powracaniu i pewne zagadki nierównowagowej mechaniki statystycznej (I)
Wymienione w tytule tematy uchodzą za trudne. Tym ważniejsze jest zacząć od rzeczy prostych i powszechnie znanych...

Weźmy pewien zbiór o skończonej liczbie elementów i jego różnowartościowe przekształcenie na siebie, czyli permutację. Dla lepszego efektu wizualnego będziemy sobie wyobrażać zbiór czarnych lub białych kwadratów wypełniających pola kwadratowej tablicy 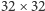 oraz permutację, dla której w
oraz permutację, dla której w 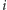 -tym wierszu i
-tym wierszu i 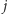 -tej kolumnie tablicy umieszczamy kwadrat poprzednio znajdujący się w wierszu o numerze
-tej kolumnie tablicy umieszczamy kwadrat poprzednio znajdujący się w wierszu o numerze 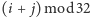 oraz kolumnie o numerze
oraz kolumnie o numerze 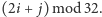 Wyniki wielokrotnego złożenia takiej permutacji dla pewnego wyjściowego ułożenia kwadratów przedstawione są na rysunku 1: po wykonaniu 32 iteracji otrzymujemy taki sam wzór jak na początku.
Wyniki wielokrotnego złożenia takiej permutacji dla pewnego wyjściowego ułożenia kwadratów przedstawione są na rysunku 1: po wykonaniu 32 iteracji otrzymujemy taki sam wzór jak na początku.

Rys. 1
Czy podobne efekty - powracanie zbioru do stanu wyjściowego po wielokrotnym wykonaniu pewnego przekształcenia - możemy zaobserwować także dla zbiorów nieskończonych? Aby odpowiedzieć na to, intuicyjnie zrozumiałe, ale nie do końca precyzyjne pytanie, przypatrzmy się jeszcze trzem dość prostym przykładom.
Obrót na okręgu
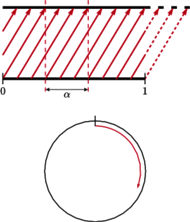
Rys. 2 Obrót na okręgu
Niezbyt skomplikowanym przykładem zbioru nieskończonego jest odcinek ![|[0, 1].](/math/temat/matematyka/analiza/uklady_dynamiczne/2015/07/15/Twierdzenie_o_powracaniu/1x-8efbc2cde3cc1692a60771c187421a78c4956e87-im-33,33,33-FF,FF,FF.gif) Żeby uniknąć kłopotów związanych z tym, iż odcinek ma końce, możemy utożsamić jego lewy koniec z prawym - otrzymamy wtedy okrąg długości 1, którego punkty ponumerowane są liczbami rzeczywistymi od 0 do 1 (tyle że jedynkę skleiliśmy z zerem). Dla takiego okręgu oraz
Żeby uniknąć kłopotów związanych z tym, iż odcinek ma końce, możemy utożsamić jego lewy koniec z prawym - otrzymamy wtedy okrąg długości 1, którego punkty ponumerowane są liczbami rzeczywistymi od 0 do 1 (tyle że jedynkę skleiliśmy z zerem). Dla takiego okręgu oraz 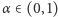 określimy przekształcenie
określimy przekształcenie 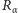 następującym wzorem:
następującym wzorem:

Symbol części całkowitej 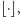 występujący w tej definicji, zapewnia, że gdy liczba
występujący w tej definicji, zapewnia, że gdy liczba 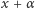 przekracza 1, przekształcenie
przekracza 1, przekształcenie 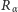 umieszcza ją z powrotem na odcinku
umieszcza ją z powrotem na odcinku ![[0,1]](/math/temat/matematyka/analiza/uklady_dynamiczne/2015/07/15/Twierdzenie_o_powracaniu/8x-8efbc2cde3cc1692a60771c187421a78c4956e87-im-33,33,33-FF,FF,FF.gif) w takiej samej odległości od 0, w jakiej liczba
w takiej samej odległości od 0, w jakiej liczba 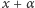 znajduje się "na prawo" od 1. Z tego względu przekształcenie
znajduje się "na prawo" od 1. Z tego względu przekształcenie 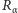 możemy wyobrażać sobie jako przesuwanie punktów naszego okręgu o odcinek
możemy wyobrażać sobie jako przesuwanie punktów naszego okręgu o odcinek 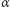 (Rys. 2). Jeżeli
(Rys. 2). Jeżeli 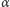 jest liczbą wymierną, którą możemy zapisać w postaci ułamka nieskracalnego
jest liczbą wymierną, którą możemy zapisać w postaci ułamka nieskracalnego 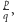 nietrudno będzie przekonać się, że po
nietrudno będzie przekonać się, że po 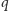 -krotnym wykonaniu przekształcenia
-krotnym wykonaniu przekształcenia 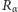 każdy punkt okręgu wróci na swoje wyjściowe miejsce. Możemy tę własność powracania wyrazić w mądry sposób, mówiąc, że dla dowolnego punktu
każdy punkt okręgu wróci na swoje wyjściowe miejsce. Możemy tę własność powracania wyrazić w mądry sposób, mówiąc, że dla dowolnego punktu 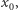 leżącego na okręgu, jego dodatnia orbita
leżącego na okręgu, jego dodatnia orbita

przechodzi przez punkt 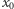 (oznaczamy
(oznaczamy 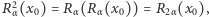
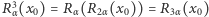 itd.). Dla
itd.). Dla 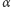 niewymiernego tak sformułowana własność powracania nie zachodzi, nie sposób się jednak oprzeć wrażeniu, że w wyniku wielokrotnego przekształcania punkt
niewymiernego tak sformułowana własność powracania nie zachodzi, nie sposób się jednak oprzeć wrażeniu, że w wyniku wielokrotnego przekształcania punkt 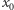 powróci "w pobliże" swego położenia wyjściowego. Możemy to wyrazić następującym stwierdzeniem
powróci "w pobliże" swego położenia wyjściowego. Możemy to wyrazić następującym stwierdzeniem
Twierdzenie (Własność powracania). Dla dowolnego punktu początkowego 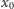 i dowolnego jego otoczenia
i dowolnego jego otoczenia 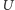 orbita
orbita 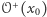 przecina
przecina 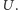
Używając mądrych słów, moglibyśmy powiedzieć, że 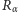 ma własność topologicznej tranzytywności oraz że jest przekształceniem prawie okresowym.
ma własność topologicznej tranzytywności oraz że jest przekształceniem prawie okresowym.
Skośny obrót torusa

Rys. 3 Sklejenie przeciwległych boków kwadratu zgodnie z kierunkiem strzałek daje torus.
Innym prostym przykładem zbioru nieskończonego jest kwadrat o boku 1. Żeby nie kłopotać się jego brzegiem, wykonamy operację podobną do sklejania końców odcinka, tyle że teraz należy skleić przeciwległe boki tak, by kierunki strzałek na rysunku 3 się zgadzały. W ten sposób otrzymujemy torus. Punkty tego torusa możemy opisać dwiema współrzędnymi 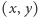 odpowiednich punktów kwadratu, przy czym
odpowiednich punktów kwadratu, przy czym 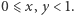 Na torusie możemy zdefiniować następujące przekształcenie:
Na torusie możemy zdefiniować następujące przekształcenie:

przyporządkowujące danemu punktowi torusa pewien inny punkt. Ponieważ współrzędna 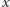 nie zmienia się przy tym przekształceniu, działanie
nie zmienia się przy tym przekształceniu, działanie 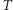 sprowadza się do przesuwania punktów odcinka
sprowadza się do przesuwania punktów odcinka 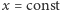 o
o 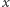 "w górę" (lub, równoważnie, obrotu odpowiedniego okręgu o
"w górę" (lub, równoważnie, obrotu odpowiedniego okręgu o 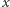 ), a zatem przekształcenia rozważanego w poprzednim przykładzie. Wynika stąd, że sformułowana powyżej własność powracania jest spełniona także dla przekształcenia
), a zatem przekształcenia rozważanego w poprzednim przykładzie. Wynika stąd, że sformułowana powyżej własność powracania jest spełniona także dla przekształcenia 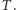
Siodło-węzeł na okręgu
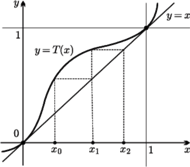
Rys. 4 Wykres funkcji

oraz graficzny sposób znajdowania wartości kolejnych iteracji tego przekształcenia.
Po tej rozgrzewce możemy przystąpić do analizy nieco trudniejszego przykładu. Rozważmy przekształcenie 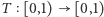 określone wzorem:
określone wzorem:

Możemy uważać je za różnowartościowe przekształcenie okręgu na siebie. Jak wyglądają orbity tego przekształcenia? Najprościej przekonać się o tym, rysując wykres 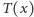 i pamiętając, że
i pamiętając, że 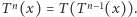 Wynik iterowania przekształcenia
Wynik iterowania przekształcenia 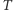 dla pewnego dowolnie wybranego punktu
dla pewnego dowolnie wybranego punktu 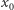 przedstawiony jest na rysunku 4. Widzimy, że dla dowolnego punktu początkowego
przedstawiony jest na rysunku 4. Widzimy, że dla dowolnego punktu początkowego 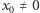 orbita
orbita 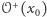 składa się z wyrazów ciągu
składa się z wyrazów ciągu 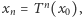 który jest zbieżny do
który jest zbieżny do 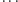 No właśnie, powiedzielibyśmy odruchowo, że jest zbieżny do 1, ale utożsamiliśmy jedynkę z zerem. Widzimy zatem, że punkt 0 ma ciekawą własność: odpycha punkty leżące odeń na prawo, a przyciąga te leżące na lewo. Przez analogię do sytuacji, z jakimi spotykamy się przy przekształceniach dwuwymiarowych, możemy nazwać go punktem typu siodło-węzeł.
No właśnie, powiedzielibyśmy odruchowo, że jest zbieżny do 1, ale utożsamiliśmy jedynkę z zerem. Widzimy zatem, że punkt 0 ma ciekawą własność: odpycha punkty leżące odeń na prawo, a przyciąga te leżące na lewo. Przez analogię do sytuacji, z jakimi spotykamy się przy przekształceniach dwuwymiarowych, możemy nazwać go punktem typu siodło-węzeł.
Łatwo zauważyć, że jedynie jednopunktowa orbita 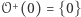 punktu 0 ma rozważaną poprzednio własność powracania. Dla
punktu 0 ma rozważaną poprzednio własność powracania. Dla 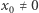 orbita
orbita 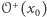 rozmija się z dostatecznie małym otoczeniem punktu
rozmija się z dostatecznie małym otoczeniem punktu 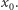
Miara
Na podstawie trzech przykładów doszliśmy do wniosku, że jedne przekształcenia mają własność powracania, a inne jej nie mają, przynajmniej w wersji, jaką podaliśmy. Czy nie da się lepiej? Czy można sformułować jakieś ogólniejsze twierdzenie dotyczące powracania? Okazuje się, że można. Niezbędne będzie do tego pojęcie miary zbioru, a dokładniej miary probabilistycznej.
Sama nazwa wskazuje na to, że pojęcie miary wprowadzono po to, by określać, jak "duży" jest zbiór. Ścisła definicja miary jest dość techniczna, choć intuicyjna, ograniczymy się zatem do podania własności miary. Otóż miara na zbiorze 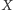 jest funkcją określoną na pewnej rodzinie podzbiorów
jest funkcją określoną na pewnej rodzinie podzbiorów 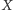 o odpowiednich własnościach. Funkcja ta, którą będziemy oznaczać przez
o odpowiednich własnościach. Funkcja ta, którą będziemy oznaczać przez 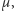 spełnia:
spełnia:
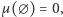
- dla
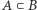 zachodzi
zachodzi 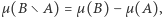
- jeśli
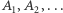 są parami rozłączne, to
są parami rozłączne, to 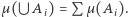
Miarę nazywamy probabilistyczną, jeśli 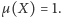
Nikt nie zdziwi się chyba, że dobrą miarą dla odcinka jest jego długość, miarą dla (otwartego) podzbioru płaszczyzny - jego pole. Rozszerzenie tej intuicji na bardziej złożone przypadki prowadzi do pojęcia miary Lebesgue'a, w które nie będziemy się bardziej szczegółowo zagłębiać. Istnieje wszakże jeszcze jeden prosty przykład miary. Każda gospodyni prowadząca tzw. salon wie, że o jego randze decyduje nie ogólna liczba gości, lecz liczba gości znamienitych. Najprostszym odpowiednikiem takiego pomysłu jest wyróżnienie w zbiorze 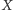 pewnego punktu
pewnego punktu 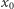 i powiedzenie, że
i powiedzenie, że 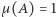 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 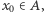 a w przeciwnym przypadku
a w przeciwnym przypadku 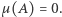 Taką miarę nazywamy miarą Diraca i oznaczamy
Taką miarę nazywamy miarą Diraca i oznaczamy 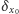 ; jej uogólnienie na dowolną skończoną liczbę wyróżnionych punktów jest oczywiste.
; jej uogólnienie na dowolną skończoną liczbę wyróżnionych punktów jest oczywiste.
Dla przekształcenia 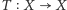 miara
miara 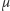 jest niezmiennicza, jeśli
jest niezmiennicza, jeśli 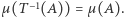 Dla obrotu na okręgu,
Dla obrotu na okręgu, 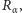 oczywistym przykładem miary niezmienniczej jest miara Lebesgue'a, w szczególności długość odcinka nie zmienia się przy równomiernym przesunięciu wszystkich punktów. Ale dla obrotu postaci
oczywistym przykładem miary niezmienniczej jest miara Lebesgue'a, w szczególności długość odcinka nie zmienia się przy równomiernym przesunięciu wszystkich punktów. Ale dla obrotu postaci 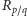 są jeszcze inne miary niezmiennicze - postaci
są jeszcze inne miary niezmiennicze - postaci
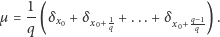 |
(*) |
Jeśli obrót jest niewymierny, jedyną miarą niezmienniczą jest miara Lebesgue'a. Spełnia ona wówczas następujące twierdzenie
Twierdzenie (Własność ergodyczności). Jeśli 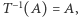 to
to 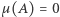 lub
lub 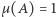 ; jedyne podzbiory niezmiennicze - zbiór pusty i cały okrąg - są trywialne w sensie miarowym.
; jedyne podzbiory niezmiennicze - zbiór pusty i cały okrąg - są trywialne w sensie miarowym.
W przypadku skośnego obrotu torusa naturalną miarą niezmienniczą dla 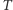 jest miara Lebesgue'a: prostokąt
jest miara Lebesgue'a: prostokąt ![|[a,b]× [c,d]](/math/temat/matematyka/analiza/uklady_dynamiczne/2015/07/15/Twierdzenie_o_powracaniu/11x-3de511805171339b8467aeeb655136572d73cd1a-im-33,33,33-FF,FF,FF.gif) jest przekształcany na równoległobok o wysokości
jest przekształcany na równoległobok o wysokości 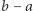 i długości podstawy
i długości podstawy  Ale istnieją też miary postaci
Ale istnieją też miary postaci
![µ([a,b] ×[c,d]) = δ ([a,b]) ⋅µ ([c,d]), x0 1](/math/temat/matematyka/analiza/uklady_dynamiczne/2015/07/15/Twierdzenie_o_powracaniu/14x-3de511805171339b8467aeeb655136572d73cd1a-dm-33,33,33-FF,FF,FF.gif)
gdzie 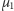 jest miarą Lebesgue'a na okręgu (miary "skupione" na okręgu danym przez
jest miarą Lebesgue'a na okręgu (miary "skupione" na okręgu danym przez 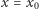 ) lub, dla
) lub, dla 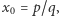 miarą daną wzorem
miarą daną wzorem 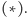
Interesują nas często "typowe" własności, spełnione dla prawie każdego obiektu. Istnieją dwa sposoby rozumienia tego zwrotu: "prawie każdy" oznacza każdy z wyjątkiem elementów skończonego zbioru punktów lub każdy z wyjątkiem elementów pewnego zbioru miary zero. Będziemy się dalej posługiwać drugim znaczeniem tego zwrotu. Możemy teraz sformułować pewne bardzo ważne twierdzenie.
Twierdzenie (Poincarégo o powracaniu). Niech przekształcenie 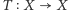 zachowuje probabilistyczną miarę
zachowuje probabilistyczną miarę 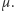 Wtedy dla każdego zbioru
Wtedy dla każdego zbioru 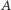 o mierze
o mierze 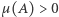 prawie każdy punkt
prawie każdy punkt 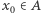 powraca do
powraca do 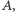 tzn. dla pewnego
tzn. dla pewnego 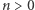 zachodzi
zachodzi 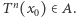
Dowód. Niech 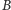 będzie zbiorem tych punktów
będzie zbiorem tych punktów 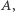 które nigdy nie powracają do
które nigdy nie powracają do 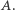 W szczególności, dla
W szczególności, dla 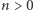 i
i 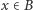 mamy
mamy 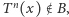 czyli
czyli 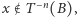 a więc
a więc 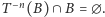 Stąd
Stąd

Analogicznie, dla dowolnego 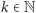 zachodzi
zachodzi 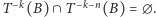 Zatem zbiory postaci
Zatem zbiory postaci 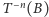 są parami rozłączne oraz mają taką samą miarę. Gdyby zachodziło
są parami rozłączne oraz mają taką samą miarę. Gdyby zachodziło 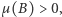 to z własności c) w definicji miary mielibyśmy
to z własności c) w definicji miary mielibyśmy 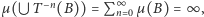 co byłoby sprzeczne z tym, że
co byłoby sprzeczne z tym, że 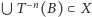 oraz
oraz 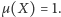 Musi zatem zachodzić
Musi zatem zachodzić 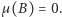
Teraz możemy na nowo rozważyć siodło-węzeł na okręgu. Zero musi się znajdować w każdym podzbiorze 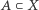 o dodatniej mierze niezmienniczej. Ale wtedy zwrot prawie każdy punkt
o dodatniej mierze niezmienniczej. Ale wtedy zwrot prawie każdy punkt 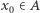 oznacza, że
oznacza, że 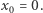 Ten punkt nie opuszcza zbioru
Ten punkt nie opuszcza zbioru 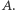
Przekształcenie piekarza

Rys. 5 Przekształcenie piekarza
Omówione na wstępie przykłady ilustrują dość szczególne mechanizmy powracania. Warto uzupełnić tę listę jeszcze jednym przykładem. Rozważmy przekształcenie kwadratu jednostkowego dane wzorem

Działanie tego przekształcenia pokazano na rysunku 5: spłaszcza i rozciąga ono wyjściowy kwadrat do prostokąta o podstawie 2 i wysokości 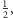 następnie rozcina uzyskany prostokąt na dwa prostokąty o podstawie 1, a w końcu układa te prostokąty jeden na drugim, tak że znowu powstaje kwadrat jednostkowy. Z uwagi na to rozciąganie i ściskanie (operacje doskonale znane każdemu, kto kiedykolwiek wyrabiał ciasto drożdżowe) przekształcenie piekarza zachowuje (dwuwymiarową) miarę Lebesgue'a. Okazuje się, że przekształcenie to ma następującą własność
następnie rozcina uzyskany prostokąt na dwa prostokąty o podstawie 1, a w końcu układa te prostokąty jeden na drugim, tak że znowu powstaje kwadrat jednostkowy. Z uwagi na to rozciąganie i ściskanie (operacje doskonale znane każdemu, kto kiedykolwiek wyrabiał ciasto drożdżowe) przekształcenie piekarza zachowuje (dwuwymiarową) miarę Lebesgue'a. Okazuje się, że przekształcenie to ma następującą własność
Twierdzenie (Własność mieszania).

czyli po dużej liczbie iteracji przekształcenia 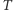 obraz
obraz 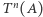 dowolnego zbioru
dowolnego zbioru 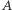 rozkłada się prawie równomiernie po całym kwadracie.
rozkłada się prawie równomiernie po całym kwadracie.
Własność mieszania jest silniejsza od własności ergodyczności; ta druga wynika z pierwszej. W szczególności obrót niewymierny na okręgu nie jest mieszający, chociaż jest ergodyczny.
Podsumowanie
Chociaż dowód twierdzenia Poincarégo o powracaniu wydaje się oczywisty i mało subtelny, twierdzenie to wywoływało (i najwidoczniej nadal wywołuje) dyskusje natury filozoficznej. Są one najczęściej związane z próbami zastosowania go do układów złożonych z dużej liczby cząstek - standardowym przykładem jest gaz skupiony w połówce zbiornika, z którego usuwamy przegrodę. Tymi tematami zajmiemy się w drugiej części artykułu.