Opisana wyżej analogia, choć prosta, nie uwzględnia jednak tego, że spin jest wielkością kwantową. Teoria kwantowa przewiduje zaś, że w przestrzeni występują nieustanne fluktuacje polegające na narodzinach i zniknięciach par cząstka-antycząstka. Efekty te wpływają minimalnie na tempo, w jakim spin danej cząstki obraca się w polu magnetycznym. To ostatnie można w wielu przypadkach bardzo dokładnie zmierzyć i stąd wynika jeden z najważniejszych problemów aktualnej teorii cząstek elementarnych, czyli Modelu Standardowego.

Tempo obiegu spinu w polu magnetycznym cząstek takich jak elektron czy mion można w zasadzie obliczyć w Modelu Standardowym i porównać z wynikami doświadczalnymi. Dla elektronu wielkość ta jest obliczona i zmierzona z dokładnością do trzynastu (!) cyfr znaczących, przy czym wyniki pomiarów i obliczeń są zgodne. Z mionem jest wszakże kłopot - przy obecnej dokładności eksperymentów na poziomie jedenastu cyfr znaczących występuje drobna acz istotna różnica z obliczeniami teoretycznymi (na ostatnim miejscu). Z uwagi na oznaczenia, jakich fizycy używają w pisanych z tej okazji równaniach, problem ten jest znany jako anomalia 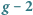dla mionu.

Zauważmy na marginesie, że w bieżącym roku mija 70. rocznica podania (przez P. Kuscha i H.M. Foleya) pierwszego kwantowego obliczenia opisywanej wielkości dla elektronu. W kolejnych dekadach rozwój teorii cząstek elementarnych i metod zaawansowanych obliczeń kwantowych doprowadził do uzyskania dokładności, z jaką nie jest przewidywana żadna inna wielkość fizyczna i która nie przestaje cokolwiek onieśmielać piszącego te słowa.

Historia obliczeń teoretycznych 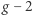dla mionu jest ciekawa sama w sobie i obfituje w zażarte dyskusje czy nieoczekiwane zmiany znaków. Głównym powodem trudności tych obliczeń jest fakt, że kwantowe fluktuacje przestrzeni powodują powstawanie par cząstka-antycząstka oddziałujących silnie, a z opisem takich układów przez Model Standardowy występują pewne praktyczne trudności obliczeniowe. Można je jednak pokonać, odwołując się do bardzo dokładnych danych doświadczalnych dla rozpraszania elektronów i pozytonów przy niskich energiach, toteż od kilku lat panuje przekonanie, że przewidywanie teoretyczne dla 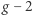mionu, wynikające z Modelu Standardowego, jest godne zaufania.

Pesymiści mówią - klapa! Model Standardowy nie zgadza się z doświadczeniem. Optymiści na to - świetnie! To znak, że w kwantowych fluktuacjach przestrzeni powstają nowe, nieodkryte jeszcze bezpośrednio cząstki. Jesteśmy blisko przełomu doświadczalnego! Kto ma rację?

A może niezgodności wcale nie ma? Na początku tego roku Takahiro Morishima, Toshifumi Futamase i Hirohiko Shimizu upublicznili w repozytorium arXiv serię trzech raportów. Japońscy badacze twierdzili w nich, że przy tak dokładnych obliczeniach, jakie potrzebne są do wyznaczenia 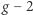dla mionu, nie można udawać, że eksperymenty wykonywane są w pustej - a więc, w myśl ogólnej teorii względności, płaskiej - przestrzeni. Ich zdaniem, należy uwzględnić niewielkie poprawki wynikające z obecności pola grawitacyjnego Ziemi. Jeśliby włączyć takie poprawki do obliczeń zaproponowaną przez nich metodą, rozbieżność między obliczeniami teoretycznymi i wynikami doświadczalnymi dla mionu znika, przy czym nie psuje się analogiczna zgodność dla elektronu. Różne efekty dla tych dwóch cząstek wynikają z tego, że badane w eksperymentach miony, w odróżnieniu od elektronów, poruszają się z prędkościami bliskimi prędkości światła.

Wynik ten zaintrygował wielu fizyków. Nie tylko dlatego, że wydawał się usuwać anomalię 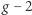dla mionu, ale przede wszystkim dlatego, że sugerował zaskakująco duży wpływ ogólnej teorii względności na świat cząstek elementarnych. Podejrzany wydawał się także fakt, że to pole grawitacyjne Ziemi miało mieć decydujący wpływ na wielkość poprawek, podczas gdy wpływ grawitacji Słońca powinien być kilkanaście razy większy, a wpływ grawitacji Galaktyki - kilka tysięcy razy większy.

Nic więc dziwnego, że wielu badaczy postanowiło sprawdzić wynik grupy japońskiej. Już po kilku dniach zaczęły ukazywać się prace, których autorzy wykazali, że, odpowiednio rozważając zasadę względności Einsteina, można mówić o wpływie grawitacji na eksperymenty mionowe tylko wtedy, gdy oddziaływania grawitacyjne zmieniają się w obszarze laboratorium, skąd wynika, że oryginalnie opublikowany efekt powinien być pomnożony przez kwadrat stosunku rozmiaru laboratorium i promienia Ziemi, a więc przez bardzo małą liczbę. Oznacza to, że postulowane rozwiązanie anomalii 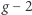dla mionu nie może być poprawne.

Czego nas uczy ta historia? Według mnie, można wyciągnąć z niej dwie lekcje. Po pierwsze, wieści o wynikach, które są zaskakujące lub w jakiś sposób "dziwne", bardzo szybko rozchodzą się w środowisku naukowym. Jednak w odróżnieniu od nieprawdziwych informacji dotyczących spraw politycznych lub społecznych, które zaskakująco skutecznie infekują świadomość społeczną, te "dziwne" wieści naukowe poddawane są szybko i skutecznie kontroli innych badaczy. W środowisku naukowym ceni się bowiem nie tych, co głośno krzyczą, ale tych, co mają (ostatecznie) rację.