Thouless/Haldane/Kosterlitz

Ciekawostki o laureatach

Wszyscy laureaci są z pochodzenia Brytyjczykami i rozpoczynali swą karierę naukową na Wyspach. Najważniejszą inspiracją do badań było dla nich rozwiązywanie teoretycznych zagadek i łamigłówek, bez szczególnego zwracania uwagi na praktyczne zastosowania. Jak podsumował Duncan Haldane w jednym z pierwszych wywiadów, "zazwyczaj ciężko jest powiedzieć, czy coś będzie użyteczne, czy też nie, ale można łatwo poznać, że coś jest intrygujące".

Powodowani ciekawością podejmowali coraz trudniejsze wyzwania naukowe, często takie, o których nikt inny nie odważył się nawet pomyśleć. Co ciekawe, jeden z noblistów ma też znaczące dokonania we wspinaczce alpejskiej. Na forach brytyjskich wspinaczy można odnaleźć pełne zdziwienia wykrzykniki: "słyszeliście, że ten Mike od Szczeliny Kosterlitza, co się z nim wspinałem w latach 70., dostał w tym roku Nobla?".

Niestety, właśnie w latach 70. kryzys ekonomiczny poważnie dotknął Wielką Brytanię i wszyscy trzej nobliści opuścili swój kraj pochodzenia, emigrując do USA. Tam też, po kilku latach, znaleźli stałe posady i tam też dokonali swoich największych odkryć. Do dziś bardzo aktywnym badaczem jest najmłodszy z całej trójki, Duncan, który z oddaniem poświęca się wykładom dla studentów (stawił się na swoim wykładzie w Princeton w dniu przyznania nagrody), można także odnaleźć w internecie inspirujące prezentacje dotyczące jego najnowszych odkryć.

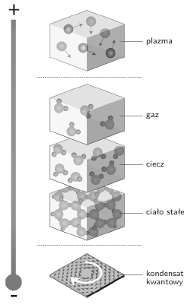
Stany skupienia materii

Fazy materii i porządek

Kluczowym pojęciem, którego zrozumienie pozwoli nam zapoznać się z odkryciami laureatów, jest pojęcie fazy materii. Na co dzień spotykamy materię w stanie gazowym, ciekłym bądź stałym; każdy z nich jest inny i przejście z jednej fazy do drugiej jest dla nas łatwo zauważalne. W ramach żartobliwego eksperymentu myślowego możemy wyobrazić sobie mocno rozgrzaną patelnię, na którą wrzucimy kostki lodu. Faktycznie, wszystkie trzy znane nam stany skupienia wody wystąpią jednocześnie.

Własnością, która wyróżnia stany materii, czy też w ogólniejszym ujęciu fazy materii, jest występowanie (lub nie) odpowiedniego uporządkowania. Przykładowo, cząsteczki wody w lodzie są ułożone w regularną sieć krystaliczną, a w gazie pary wodnej poruszają się zupełnie chaotycznie. Centralnym zagadnieniem teorii materii faz skondensowanych, w ramach której pracowali nobliści, jest klasyfikacja i opis mogących się pojawić faz. Przejścia między fazami (takie, jak np. zamarzanie wody) nie mogą odbyć się w inny sposób niż na drodze zmiany jednego porządku na drugi, co wymaga "rewolucji", istotnego przeorganizowania.

Fazy kwantowe

W "zwyczajnych" stanach skupienia atomy, z których składa się substancja, poruszają się w sposób chaotyczny. Oczywiście, na poziomie atomowym obowiązują prawa fizyki kwantowej, często bardzo odległe od naszych klasycznych intuicji. Silnie chaotyczny ruch atomów powoduje jednak, że subtelne prawa fizyki kwantowej ulegają niejako zamazaniu, własności uśrednione względem wielu atomów danej substancji podlegają zupełnie zwyczajnemu opisowi klasycznej mechaniki.

Prawdziwym wyzwaniem jest badanie kwantowych faz materii, których własności są dalekie od naszych codziennych wyobrażeń. W celu wzmocnienia roli zjawisk kwantowych musimy ograniczyć chaotyczny ruch składowych, co osiągamy przez schładzanie substancji do bardzo niskich temperatur, możliwie najbliższych temperaturze zera bezwzględnego. Drugą możliwością jest ograniczenie wymiarowości badanego układu, w tym celu uzyskujemy bardzo cienkie warstwy powierzchniowe, międzypowierzchnie, czy wprost dwuwymiarowe materiały, takie jak np. grafen. Odkrywamy nowe, niezwykłe stany materii, których klasyfikacja umyka naszym intuicjom ukształtowanym w świecie klasycznym. Szczególnym wyzwaniem jest zrozumienie tzw. zjawisk kolektywnych, w których wiele atomów ujawnia wspólne, często nieoczekiwane, zbiorowe własności.

Nadprzewodnictwo i nadciekłość

Najbardziej spektakularnymi kwantowymi fazami materii są stan nadciekły i nadprzewodzący. W pewnych metalach, ochłodzonych poniżej charakterystycznej temperatury bliskiej zera bezwzględnego, oporność spada do zera. Obserwujemy, że raz wzbudzony prąd płynie w nadprzewodzącym pierścieniu praktycznie w nieskończoność (czyli tyle, na ile wystarczy cierpliwości wykonującym doświadczenie). Podobnie w nadciekłym helu brak lepkości i jakichkolwiek oporów ruchu powoduje, że ciecz umieszczona w naczynku podnosi się po ściankach i powoli cała wypływa. Tak niezwykłe zjawiska są możliwe dzięki powstawaniu wspólnej funkcji falowej opisującej jednocześnie wiele atomów helu (nadciekłość) czy elektronów w metalu (nadprzewodnictwo).

Przejście KT

Na podstawie wiedzy zgromadzonej w latach 60. XX wieku fizycy byli przekonani, że w dwóch wymiarach (czyli w układach, które tworzą cienkie warstwy lub też w warstwach powierzchniowych) nie może istnieć żaden wyróżniony porządek, a więc nie będzie można znaleźć faz ani przejść pomiędzy nimi - materia będzie zachowywała się cały czas równie nieciekawie. Tymczasem Michael Kosterlitz i David Thouless (w skrócie: KT) wykazali, że taki porządek istnieje oraz wskazali mechanizm przejścia pomiędzy dwiema fazami: uporządkowaną i nieuporządkowaną.

Układ będący w fazie nadciekłej (lub nadprzewodzącej) można przedstawić za pomocą modelu pola strzałek, które wskazują kierunek w płaszczyźnie. Mówimy, że jest to model efektywny, ujmujący tylko najistotniejsze cechy układu (czyli np. takie, które decydują o własnościach termicznych). Wspólnie ułożone strzałki, wskazujące jeden kierunek, odpowiadają fazie nadciekłej (lub nadprzewodzącej).

Okazuje się, że ważną rolę w takim układzie pełnią wiry istniejące w dwuwymiarowym świecie. W niskich temperaturach wiry występują zawsze w parach i poruszają się wspólnie. Przy pewnej, podwyższonej temperaturze korzystniejsze staje się jednak rozdzielenie wirów, które zaczynają poruszać się niezależenie. Liczba wirów rośnie z temperaturą i oczywiste jest, że faza z dużą liczbą niezależnych wirów będzie wyglądać w sposób nieuporządkowany. Teoria wyprowadzona przez KT opisuje ilościowo zjawisko pojawiania się samotnych wirów, które prowadzi do przeorganizowania całego układu. Zadziwiające jest, że teoria ta przewiduje bardzo proste, uniwersalne prawo: gdzie 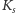jest tzw. sztywnością kondensatu (czyli zmianą energii związaną z małym skręceniem wspólnego kierunku strzałek), to stała Boltzmanna, natomiast jest temperaturą, w której następuje przejście KT. Prawo to zostało sprawdzone dla wielu układów doświadczalnych: warstw nadciekłego helu, granularnych nadprzewodników, ale też warstw ciekłych kryształów oraz magnetyków.

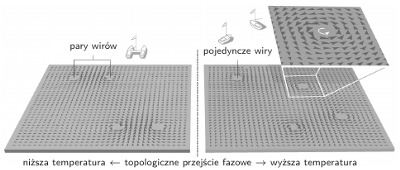
Topologiczne przejście fazowe w warstwie zimnej materii. Poniżej temperatury przejścia fazowego, wiry występują w parach, a powyżej pojedyncze wiry poruszają się swobodnie.

Wir jako obiekt topologiczny

Najważniejszym obiektem, który pojawia się w matematycznym sformułowaniu teorii KT, jest wir dwuwymiarowych strzałek. Wyobraźmy sobie, że okrążamy środek wiru wzdłuż pewnej zamkniętej krzywej i w trakcie naszej podróży notujemy kierunek pola strzałek. Łatwo spostrzec, że strzałka obróci się o pełny kąt. Gdybyśmy jednak zmienili plan naszej podróży, i nie okrążyli środka wiru - wtedy strzałka nie wykona pełnego obrotu. Wielkość, która mierzy "ile razy" obróciła się strzałka, nosi nazwę indeksu nawinięć. Obiekty matematyczne, które można charakteryzować wielkościami podobnymi do indeksu nawinięć, to jeden z przedmiotów badań topologii. Nasz dwuwymiarowy wir jest tu najprostszym przykładem, wśród fizyków nosi on nazwę defektu topologicznego. Co ciekawe, kolejne uogólnienie indeksu nawinięć, tym razem na pole trójwymiarowych strzałek zaczepionych na sferze, też zostało zastosowane w badaniach noblistów z 2016 roku.

Oczywiście, okazuje się, że odkrycie Kosterliza i Thoulessa było niejako pierwszym, małym krokiem w długiej przygodzie fizyków materii skondensowanej z indeksami topologicznymi i dziwnymi, kwantowymi fazami. David Thouless otrzymał swoją "drugą ćwiartkę" nagrody za sklasyfikowanie faz kwantowego efektu Halla. Z kolei Duncan Haldane opisał fazy magnetyczne łańcuchów atomowych - rozszerzając podejście KT, i też uzyskując wyniki idące pod prąd współczesnych mu przewidywań teoretycznych (jednak pomyślnie zweryfikowane w eksperymentach kilka lat później). Wśród badaczy coraz częściej mówi się dziś o topologicznych izolatorach i topologicznych metalach - jako o kontynuacji badań Thoulessa, Haldane'a i Kosterlitza. Kto wie, może pod tymi enigmatycznymi nazwami jeszcze innych faz kryje się materiał na kolejną opowieść?