Elementarz cząstek elementarnych
Nie każdy wie, jak działa Model Standardowy
W poprzednim odcinku omówiliśmy najważniejsze cechy Modelu Standardowego oddziaływań cząstek elementarnych. Tutaj, zgodnie z zapowiedzią, postaram się pokazać bogactwo struktury teoretycznej ukrytej za prostym fenomenologicznym opisem cząstek i ich oddziaływań.
Podstawowymi obiektami, którymi operuje kwantowa teoria oddziaływań cząstek są pola. Kluczową rolę w sformułowaniu Modelu Standardowego odgrywają jednak przede wszystkim symetrie 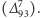 Są one różnego rodzaju. Na przykład równania tej teorii nie ulegają zmianie, jeśli trzy pola każdego z kwarków odpowiadające trzem kolorom potraktujemy jak (zespolone) składowe wektora i dokonamy jego "obrotu" w pewnej abstrakcyjnej przestrzeni koloru. Tworzona przez wszystkie takie obroty grupa
Są one różnego rodzaju. Na przykład równania tej teorii nie ulegają zmianie, jeśli trzy pola każdego z kwarków odpowiadające trzem kolorom potraktujemy jak (zespolone) składowe wektora i dokonamy jego "obrotu" w pewnej abstrakcyjnej przestrzeni koloru. Tworzona przez wszystkie takie obroty grupa 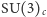 symetrii "kolorowej" (to właśnie oznacza indeks
symetrii "kolorowej" (to właśnie oznacza indeks  - chodzi o niepomylenie różnych, choć w sensie matematycznym izomorficznych grup, które pełnią jednak zupełnie inne role) jest generowana przez 8 podstawowych "ruchów", czyli ma ona 8 generatorów. W teorii pola istnieje jeszcze dodatkowa możliwość polegająca na tym, że wszystkie pola kwarkowe jednocześnie obracamy w przestrzeni koloru o "kąt", który nie jest stały, lecz zmienia się od punktu do punktu czasoprzestrzeni. Okazuje się, że równania mogą nadal być niezmiennicze względem takich lokalnych obrotów, jeśli oprócz obracanych pól istnieją jeszcze inne pola, po jednym na każdy generator grupy, które obracają się jednocześnie z tamtymi w odpowiedni sposób. W przypadku grupy koloru tymi dodatkowymi polami są właśnie pola gluonów. Teoria, której równania wykazują symetrię względem takich lokalnych obrotów pól, nazywa się fachowo teorią z cechowaniem. Będąca częścią Modelu Standardowego teoria oddziaływań kwarków i gluonów, zwana chromodynamiką kwantową (QCD), która w zasadzie opisuje wszystkie zjawiska związane z oddziaływaniami silnymi (a więc i właściwości olbrzymiej liczby rezonansów barionowych i mezonowych oraz ich oddziaływania), jest zatem teorią z grupą cechowania
- chodzi o niepomylenie różnych, choć w sensie matematycznym izomorficznych grup, które pełnią jednak zupełnie inne role) jest generowana przez 8 podstawowych "ruchów", czyli ma ona 8 generatorów. W teorii pola istnieje jeszcze dodatkowa możliwość polegająca na tym, że wszystkie pola kwarkowe jednocześnie obracamy w przestrzeni koloru o "kąt", który nie jest stały, lecz zmienia się od punktu do punktu czasoprzestrzeni. Okazuje się, że równania mogą nadal być niezmiennicze względem takich lokalnych obrotów, jeśli oprócz obracanych pól istnieją jeszcze inne pola, po jednym na każdy generator grupy, które obracają się jednocześnie z tamtymi w odpowiedni sposób. W przypadku grupy koloru tymi dodatkowymi polami są właśnie pola gluonów. Teoria, której równania wykazują symetrię względem takich lokalnych obrotów pól, nazywa się fachowo teorią z cechowaniem. Będąca częścią Modelu Standardowego teoria oddziaływań kwarków i gluonów, zwana chromodynamiką kwantową (QCD), która w zasadzie opisuje wszystkie zjawiska związane z oddziaływaniami silnymi (a więc i właściwości olbrzymiej liczby rezonansów barionowych i mezonowych oraz ich oddziaływania), jest zatem teorią z grupą cechowania 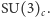 Symetria cechowania jednoznacznie wyznacza strukturę elementarnych oddziaływań kwarków z gluonami i gluonów między sobą. Symetria ta realizuje się w świecie kwarków ściśle, co oznacza np. że kwarki różniące się tylko kolorem mają taką samą masę, a amplitudy rozpraszania kwarków o różnych kolorach można jedne z drugich otrzymać przez odpowiednie przekształcenie. Ponieważ symetria cechowania QCD jest ścisła, gluony muszą być cząstkami o masie równej zeru.
Symetria cechowania jednoznacznie wyznacza strukturę elementarnych oddziaływań kwarków z gluonami i gluonów między sobą. Symetria ta realizuje się w świecie kwarków ściśle, co oznacza np. że kwarki różniące się tylko kolorem mają taką samą masę, a amplitudy rozpraszania kwarków o różnych kolorach można jedne z drugich otrzymać przez odpowiednie przekształcenie. Ponieważ symetria cechowania QCD jest ścisła, gluony muszą być cząstkami o masie równej zeru.
Ważną cechą oddziaływania gluonów jest to, że oddziaływania te stają się tym silniejsze, im dalej od siebie znajdują się kwarki wymieniające między sobą gluony. W duchu zasady nieoznaczoności Heisenberga 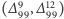 oznacza to, że kwarki oddziałują tym silniej, im mniejszy jest przekaz pędu i energii pomiędzy nimi. Skutkiem tego jest zjawisko uwięzienia kwarków
oznacza to, że kwarki oddziałują tym silniej, im mniejszy jest przekaz pędu i energii pomiędzy nimi. Skutkiem tego jest zjawisko uwięzienia kwarków 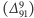 - nie są one nigdy obserwowane jako cząstki swobodne i zawsze tworzą układy związane, które nazywa się hadronami (cząstki oddziałujące silnie); względem grupy koloru są one tym, czym elektrycznie obojętne atomy względem grupy
- nie są one nigdy obserwowane jako cząstki swobodne i zawsze tworzą układy związane, które nazywa się hadronami (cząstki oddziałujące silnie); względem grupy koloru są one tym, czym elektrycznie obojętne atomy względem grupy 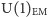 elektromagnetyzmu. Układami takimi mogą być albo
elektromagnetyzmu. Układami takimi mogą być albo 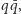 czyli mezony, albo
czyli mezony, albo 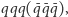 czyli bariony (antybariony). Ostatnio okazało się
czyli bariony (antybariony). Ostatnio okazało się 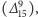 choć sygnały były już wcześniej
choć sygnały były już wcześniej 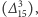 że możliwe są także układy
że możliwe są także układy 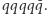 Hadrony (bariony, antybariony i mezony) są więc wszystkie układami złożonymi (w tym sensie nie są one prawdziwie elementarne).
Hadrony (bariony, antybariony i mezony) są więc wszystkie układami złożonymi (w tym sensie nie są one prawdziwie elementarne).
Jeśli pominąć masy kwarków i rozpatrywać QCD oddzielnie od reszty Modelu Standardowego, staje się ona teorią, której wszystkie przewidywania zależą od wartości jednego parametru bezwymiarowego, jakim jest stała sprzężenia 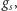 wyznaczana doświadczalnie. Wartość tę można za pomocą teorii przetłumaczyć na pewną skalę energii (lub, zgodnie ze wzorem
wyznaczana doświadczalnie. Wartość tę można za pomocą teorii przetłumaczyć na pewną skalę energii (lub, zgodnie ze wzorem 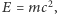 masy)
masy) 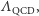 która ustanawia bezwzględną miarę energii dla oddziaływań silnych. Okazuje się, że
która ustanawia bezwzględną miarę energii dla oddziaływań silnych. Okazuje się, że 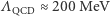 .
.

Przykład chromodynamiki kwantowej pozwala poznać jeszcze jeden sposób, w jaki symetria może realizować się w kwantowej teorii pola. Gdyby masy kwarków były ściśle zerowe, wszystkie kwarki (tego samego koloru) o tej samej skrętności byłyby zupełnie identyczne - nie byłoby sposobu, by odróżnić np. lewoskrętny czerwony kwark  od lewoskrętnego czerwonego
od lewoskrętnego czerwonego 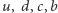 lub
lub 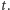 Wprawdzie masy kwarków
Wprawdzie masy kwarków 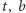 i
i  trudno uznać za zerowe, ale masy kwarków
trudno uznać za zerowe, ale masy kwarków 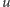 i
i 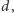 a nawet
a nawet 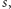 można uznać za pomijalne w porównaniu ze skalą
można uznać za pomijalne w porównaniu ze skalą 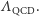 W tej granicy równania chromodynamiki są niezmiennicze względem globalnych (tj. takich samych w każdym punkcie czasoprzestrzeni) obrotów dokonywanych w przestrzeni rozpinanej przez trzy lewochiralne pola lewoskrętnych kwarków (obroty pól odpowiadających różnym kolorom są takie same) i niezależnych globalnych obrotów w przestrzeni rozpinanej przez trzy prawochiralne pola prawoskrętnych kwarków. Grupą symetrii równań chromodynamiki jest wtedy
W tej granicy równania chromodynamiki są niezmiennicze względem globalnych (tj. takich samych w każdym punkcie czasoprzestrzeni) obrotów dokonywanych w przestrzeni rozpinanej przez trzy lewochiralne pola lewoskrętnych kwarków (obroty pól odpowiadających różnym kolorom są takie same) i niezależnych globalnych obrotów w przestrzeni rozpinanej przez trzy prawochiralne pola prawoskrętnych kwarków. Grupą symetrii równań chromodynamiki jest wtedy 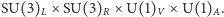 Czynnik
Czynnik 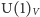 odpowiada niezmienniczości równań względem pomnożenia lewo- i prawochiralnych pól wszystkich kwarków (także tych ciężkich) przez wspólny globalny czynnik fazowy
odpowiada niezmienniczości równań względem pomnożenia lewo- i prawochiralnych pól wszystkich kwarków (także tych ciężkich) przez wspólny globalny czynnik fazowy 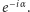 W czystej chromodynamice symetria ta jest ścisła. Konsekwencją jej jest zachowywanie liczby barionowej we wszystkich reakcjach uwarunkowanych oddziaływaniami silnymi (i elektromagnetycznymi). Nie jest ono jednak, ściśle rzecz biorąc, symetrią całego Modelu Standardowego, ale w warunkach laboratoryjnych procesy, w których liczba barionowa nie byłaby zachowana, są praktycznie niemożliwe; były one jednak częste w wysokich temperaturach, jakie panowały we wczesnym wszechświecie i musiały odegrać ważną rolę w powstaniu obserwowanej dziś przewagi materii nad antymaterią.
W czystej chromodynamice symetria ta jest ścisła. Konsekwencją jej jest zachowywanie liczby barionowej we wszystkich reakcjach uwarunkowanych oddziaływaniami silnymi (i elektromagnetycznymi). Nie jest ono jednak, ściśle rzecz biorąc, symetrią całego Modelu Standardowego, ale w warunkach laboratoryjnych procesy, w których liczba barionowa nie byłaby zachowana, są praktycznie niemożliwe; były one jednak częste w wysokich temperaturach, jakie panowały we wczesnym wszechświecie i musiały odegrać ważną rolę w powstaniu obserwowanej dziś przewagi materii nad antymaterią.
Przyjmuje się jednak, że nawet przy ściśle zerowych masach kwarków 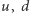 i
i  nie cała zapachowa symetria jest odzwierciedlona w świecie fizycznych hadronów i w ich oddziaływaniach silnych. Jej część musi być "popsuta" przez dynamiczne formowanie się, wskutek oddziaływań silnych, przenikającego całą przestrzeń stałego kondensatu pól reprezentujących związane pary lewoskrętnych kwarków i prawoskrętnych antykwarków, gdyż inaczej musiałyby istnieć dodatkowe multiplety hadronów, które w rzeczywistości nie istnieją. Kondensat ten jest właściwością kwantowego stanu o najniższej energii układu pól kwarkowo-gluonowych. O takiej sytuacji mówi się, że część symetrii równań jest spontanicznie naruszona przez stan próżni (zob.
nie cała zapachowa symetria jest odzwierciedlona w świecie fizycznych hadronów i w ich oddziaływaniach silnych. Jej część musi być "popsuta" przez dynamiczne formowanie się, wskutek oddziaływań silnych, przenikającego całą przestrzeń stałego kondensatu pól reprezentujących związane pary lewoskrętnych kwarków i prawoskrętnych antykwarków, gdyż inaczej musiałyby istnieć dodatkowe multiplety hadronów, które w rzeczywistości nie istnieją. Kondensat ten jest właściwością kwantowego stanu o najniższej energii układu pól kwarkowo-gluonowych. O takiej sytuacji mówi się, że część symetrii równań jest spontanicznie naruszona przez stan próżni (zob. 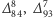 ).
).
W ramach relatywistycznej kwantowej teorii pola dowodzi się, że konsekwencją spontanicznego naruszenia niezmienniczości względem klasy przekształceń odpowiadających jakiemuś generatorowi grupy symetrii jest istnienie jednej cząstki bezmasowej o spinie zero, tzw. bozonu Nambu-Goldstone'a (NG). Wskutek istnienia kondensatu liczba "dobrych" generatorów symetrii globalnej QCD zmniejsza się o dziewięć. Można by się więc spodziewać istnienia wśród hadronów dziewięciu bezmasowych i bezspinowych stanów związanych par kwark-antykwark, czyli mezonów, będących bozonami NG. Ponieważ w rzeczywistości masy kwarków nie są ściśle zerowe, mezony te również nie powinny być całkiem bezmasowe, ale wyraźnie lżejsze niż inne hadrony. I rzeczywiście: istnieje oktet mezonów: trzy piony 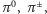 cztery kaony
cztery kaony 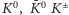 oraz mezon
oraz mezon 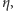 które są wyraźnie lżejsze niż pozostałe hadrony, ale brak dziewiątego lekkiego mezonu. Rozumowanie oparte na przybliżonej symetrii jest słuszne, ale symetria równań QCD odpowiadająca czynnikowi
które są wyraźnie lżejsze niż pozostałe hadrony, ale brak dziewiątego lekkiego mezonu. Rozumowanie oparte na przybliżonej symetrii jest słuszne, ale symetria równań QCD odpowiadająca czynnikowi 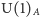 jest tylko pozorna: likwiduje ją bowiem występowanie specyficznie kwantowego efektu, czyli tzw. anomalii, i dlatego dziewiąty lekki mezon nie istnieje. Podobna anomalia powoduje, że w pełnym Modelu Standardowym, tj. po uwzględnieniu oddziaływań kwarków z bozonami
jest tylko pozorna: likwiduje ją bowiem występowanie specyficznie kwantowego efektu, czyli tzw. anomalii, i dlatego dziewiąty lekki mezon nie istnieje. Podobna anomalia powoduje, że w pełnym Modelu Standardowym, tj. po uwzględnieniu oddziaływań kwarków z bozonami 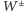 i
i 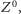 pozorna staje się symetria
pozorna staje się symetria 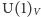 i liczba barionowa nie jest ściśle zachowaną wielkością (pozostaje jednak taką w zwykłych warunkach laboratoryjnych).
i liczba barionowa nie jest ściśle zachowaną wielkością (pozostaje jednak taką w zwykłych warunkach laboratoryjnych).
Ponieważ anomalia psuje symetrię 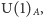 a kondensat narusza spontanicznie część pozostałej (przybliżonej) globalnej symetrii QCD, wszystkie hadrony grupują się w multiplety przybliżonej, ale nienaruszonej spontanicznie grupy
a kondensat narusza spontanicznie część pozostałej (przybliżonej) globalnej symetrii QCD, wszystkie hadrony grupują się w multiplety przybliżonej, ale nienaruszonej spontanicznie grupy 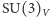 generowanej przez takie same obroty pól lewo- i prawochiralnych kwarków. Symetria ta jest psuta tylko przez różnice mas kwarków (byłaby ona ścisła, gdyby kwarki
generowanej przez takie same obroty pól lewo- i prawochiralnych kwarków. Symetria ta jest psuta tylko przez różnice mas kwarków (byłaby ona ścisła, gdyby kwarki 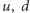 i
i  miały dokładnie równe masy). Oczywiście, ponieważ masa kwarka
miały dokładnie równe masy). Oczywiście, ponieważ masa kwarka  jest sporo większa niż kwarków
jest sporo większa niż kwarków 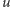 i
i 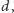 znacznie lepiej widoczne jest grupowanie się hadronów w multiplety grupy izospinu
znacznie lepiej widoczne jest grupowanie się hadronów w multiplety grupy izospinu 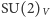 - wszystkie cząstki tych multipletów (np.
- wszystkie cząstki tych multipletów (np. 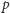 i
i 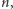 czy
czy 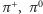 i
i 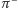 ) mają niemal równe masy. (Różnica mas
) mają niemal równe masy. (Różnica mas 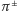 i
i 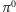 jest praktycznie w całości spowodowana efektami oddziaływań elektromagnetycznych, a nie bardzo małą różnicą mas kwarków
jest praktycznie w całości spowodowana efektami oddziaływań elektromagnetycznych, a nie bardzo małą różnicą mas kwarków 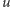 i
i 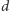 ; ta odgrywa jednak rolę w wyjaśnianiu różnicy mas
; ta odgrywa jednak rolę w wyjaśnianiu różnicy mas 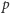 i
i 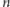 ).
).
Pozostała część Modelu Standardowego opisująca oddziaływania elektromagnetyczne i słabe oraz ich współgranie z oddziaływaniami silnymi jest, podobnie jak QCD, również teorią z cechowaniem, ale grupą cechowania jest tu 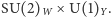 Tak jak trzy różne kolory tego samego kwarka mieszają się pod wpływem lokalnych obrotów z grupy
Tak jak trzy różne kolory tego samego kwarka mieszają się pod wpływem lokalnych obrotów z grupy 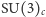 koloru, tak tu pod wpływem lokalnych obrotów z grupy
koloru, tak tu pod wpływem lokalnych obrotów z grupy 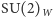 (zmieniających się od punktu do punktu w czasoprzestrzeni) mieszają się tworzące pary (tzw. dublety) dwa lewochiralne pola (np. dwa lewochiralne pola leptonów
(zmieniających się od punktu do punktu w czasoprzestrzeni) mieszają się tworzące pary (tzw. dublety) dwa lewochiralne pola (np. dwa lewochiralne pola leptonów 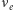 i
i 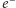 ) lub kwarków (tego samego koloru) typu górnego i dolnego (np.
) lub kwarków (tego samego koloru) typu górnego i dolnego (np.  i
i 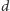 ). Podobnie pole Higgsa to cztery mieszające się ze sobą pod wpływem tych obrotów pola. Czynnik
). Podobnie pole Higgsa to cztery mieszające się ze sobą pod wpływem tych obrotów pola. Czynnik 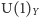 odpowiada niezmienniczości względem pomnożenia pola każdego z fermionów i pola Higgsa przez pewien (zmieniający się w czasoprzestrzeni) czynnik fazowy. Aby równania teorii były niezmiennicze względem takich lokalnych przekształceń, z każdą z czterech takich transformacji stowarzyszone jest pole bozonu pośredniczącego (cechowania) o spinie
odpowiada niezmienniczości względem pomnożenia pola każdego z fermionów i pola Higgsa przez pewien (zmieniający się w czasoprzestrzeni) czynnik fazowy. Aby równania teorii były niezmiennicze względem takich lokalnych przekształceń, z każdą z czterech takich transformacji stowarzyszone jest pole bozonu pośredniczącego (cechowania) o spinie 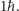 Symetria cechowania jednoznacznie wyznacza ich elementarne oddziaływania z fermionami, z bozonem Higgsa i ich oddziaływania między sobą. Stałymi sprzężenia analogicznymi do stałej
Symetria cechowania jednoznacznie wyznacza ich elementarne oddziaływania z fermionami, z bozonem Higgsa i ich oddziaływania między sobą. Stałymi sprzężenia analogicznymi do stałej 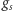 oddziaływań silnych są tu
oddziaływań silnych są tu 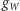 i
i 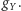 Gdyby symetria równań teorii względem tych przekształceń nie była naruszona przez stan próżni (tj. spontanicznie), nie można by było odróżnić np. lewoskrętnego neutrina elektronowego od lewoskrętnego elektronu, a cztery bozony cechowania grupy
Gdyby symetria równań teorii względem tych przekształceń nie była naruszona przez stan próżni (tj. spontanicznie), nie można by było odróżnić np. lewoskrętnego neutrina elektronowego od lewoskrętnego elektronu, a cztery bozony cechowania grupy 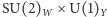 byłyby bezmasowe. Wspomniany już kondensat
byłyby bezmasowe. Wspomniany już kondensat  jednej ze składowych pola Higgsa (symetria cechowania oznacza, że nie jest istotne której!) jest źródłem spontanicznego naruszenia symetrii
jednej ze składowych pola Higgsa (symetria cechowania oznacza, że nie jest istotne której!) jest źródłem spontanicznego naruszenia symetrii 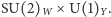 Skalę energii wyznaczaną przez wartość kondensatu,
Skalę energii wyznaczaną przez wartość kondensatu, 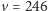 GeV, nazywa się skalą naruszenia tej symetrii, albo skalą Fermiego (używana jest też nazwa "skala elektrosłaba"). Naruszenie symetrii
GeV, nazywa się skalą naruszenia tej symetrii, albo skalą Fermiego (używana jest też nazwa "skala elektrosłaba"). Naruszenie symetrii 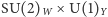 nie jest jednak całkowite: pozostają nienaruszone przekształcenia generowane przez sumę generatora grupy
nie jest jednak całkowite: pozostają nienaruszone przekształcenia generowane przez sumę generatora grupy 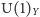 oraz jednego z generatorów grupy
oraz jednego z generatorów grupy 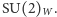 Odpowiadający tym wciąż "dobrym" przekształceniom bezmasowy bozon o spinie
Odpowiadający tym wciąż "dobrym" przekształceniom bezmasowy bozon o spinie 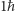 jest utożsamiony z fotonem.
jest utożsamiony z fotonem.
W odróżnieniu od omawianego wyżej spontanicznego naruszenia symetrii globalnej 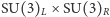 (lub mniej przybliżonej
(lub mniej przybliżonej 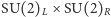 ) QCD, analogicznemu naruszeniu symetrii lokalnej (cechowania) nie towarzyszy występowanie bezmasowych bozonów NG; działa w tym przypadku tzw. mechanizm Higgsa polegający na tym, że bozony pośredniczące odpowiadające "złamanym" generatorom grupy stają się masywne, a niedoszłe bozony NG stają się brakującymi masywnymi bozonami pośredniczącymi o skrętności równej zeru. Tak właśnie dzieje się z pozostałymi trzema bozonami pośredniczącymi grupy
) QCD, analogicznemu naruszeniu symetrii lokalnej (cechowania) nie towarzyszy występowanie bezmasowych bozonów NG; działa w tym przypadku tzw. mechanizm Higgsa polegający na tym, że bozony pośredniczące odpowiadające "złamanym" generatorom grupy stają się masywne, a niedoszłe bozony NG stają się brakującymi masywnymi bozonami pośredniczącymi o skrętności równej zeru. Tak właśnie dzieje się z pozostałymi trzema bozonami pośredniczącymi grupy 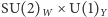 - stają się one bozonami
- stają się one bozonami 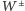 i
i 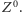 Ponieważ źródłem spontanicznego naruszenia symetrii cechowania
Ponieważ źródłem spontanicznego naruszenia symetrii cechowania 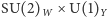 jest kondensat pola Higgsa, mechanizmem generującym masy
jest kondensat pola Higgsa, mechanizmem generującym masy 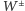 i
i 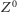 jest stałe oddziaływanie tych cząstek z tym kondensatem (pole fotonu z kondensatem nie oddziałuje), przy czym (w pierwszym przybliżeniu)
jest stałe oddziaływanie tych cząstek z tym kondensatem (pole fotonu z kondensatem nie oddziałuje), przy czym (w pierwszym przybliżeniu) 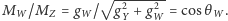 Związek ten jest jednym z ważnych przewidywań teorii. Jak już wspominałem, kwarki i leptony również stają się masywne wskutek podobnego oddziaływania.
Związek ten jest jednym z ważnych przewidywań teorii. Jak już wspominałem, kwarki i leptony również stają się masywne wskutek podobnego oddziaływania.
Oddziaływania przenoszone przez bozony 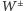 (oraz
(oraz 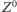 ) mają bardzo krótki zasięg
) mają bardzo krótki zasięg 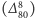 z powodu bardzo dużej masy tych cząstek. W pierwszym przybliżeniu można je więc traktować jak punktowe z efektywną stałą sprzężenia
z powodu bardzo dużej masy tych cząstek. W pierwszym przybliżeniu można je więc traktować jak punktowe z efektywną stałą sprzężenia 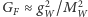 i to właśnie z powodu proporcjonalności
i to właśnie z powodu proporcjonalności 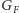 do odwrotności dużej masy są one tak "słabe". Jak powinno być jasne z powyższych rozważań, nie są one jednak na fundamentalnym poziomie istotnie różne od oddziaływań elektromagnetycznych: u podstaw jednych i drugich leży symetria cechowania. W tym sensie są one zunifikowane (zob.
do odwrotności dużej masy są one tak "słabe". Jak powinno być jasne z powyższych rozważań, nie są one jednak na fundamentalnym poziomie istotnie różne od oddziaływań elektromagnetycznych: u podstaw jednych i drugich leży symetria cechowania. W tym sensie są one zunifikowane (zob. 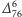 ). Nie jest to jednak unifikacja pełna, ponieważ na grupę symetrii cechowania Modelu Standardowego, związaną z oddziaływaniami elektromagnetycznymi i słabymi, składają się dwa czynniki grupowe:
). Nie jest to jednak unifikacja pełna, ponieważ na grupę symetrii cechowania Modelu Standardowego, związaną z oddziaływaniami elektromagnetycznymi i słabymi, składają się dwa czynniki grupowe: 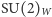 i
i 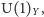 są też dwie niezależne stałe sprzężenia
są też dwie niezależne stałe sprzężenia 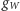 i
i 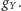 Ładunkiem elektrycznym jest kombinacja
Ładunkiem elektrycznym jest kombinacja 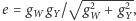 a
a 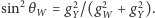
Opisany tu model standardowy 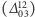 jest teorią bardzo skomplikowaną i bogatą. Daje on jednolity jakościowy, a w wielu przypadkach także znakomity ilościowy opis całego mnóstwa reakcji zachodzących między cząstkami. Szczególnym jego sukcesem jest opis tzw. procesów rzadkich, do których zaliczają się także takie, w których nie jest zachowywana parzystość kombinowana CP
jest teorią bardzo skomplikowaną i bogatą. Daje on jednolity jakościowy, a w wielu przypadkach także znakomity ilościowy opis całego mnóstwa reakcji zachodzących między cząstkami. Szczególnym jego sukcesem jest opis tzw. procesów rzadkich, do których zaliczają się także takie, w których nie jest zachowywana parzystość kombinowana CP 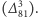 Także wchodząca w jego skład QCD, mimo iż pewnych interesujących wielkości nie udaje się przy jej użyciu obliczyć analitycznie (np. masy protonu czy przekroju czynnego rozpraszania elastycznego protonu na protonie), słabnięcie wzajemnych oddziaływań kwarków i gluonów na małych odległościach (tj. przy dużych przekazach pędu i energii) pozwala, w połączeniu z fenomenologiczną parametryzacją "zawartości" protonu za pomocą tzw. funkcji struktury, wykorzystać ją do ilościowego opisywania procesów "twardych", czyli takich, które można traktować jak bezpośrednie zderzenia indywidualnych składników rozpraszanych na sobie dwu protonów. Dzięki temu QCD wraz z całym Modelem Standardowym stała się nieodzownym schematem teoretycznym używanym przy poszukiwaniu nowych cząstek i oddziaływań w akceleratorach takich jak LHC.
Także wchodząca w jego skład QCD, mimo iż pewnych interesujących wielkości nie udaje się przy jej użyciu obliczyć analitycznie (np. masy protonu czy przekroju czynnego rozpraszania elastycznego protonu na protonie), słabnięcie wzajemnych oddziaływań kwarków i gluonów na małych odległościach (tj. przy dużych przekazach pędu i energii) pozwala, w połączeniu z fenomenologiczną parametryzacją "zawartości" protonu za pomocą tzw. funkcji struktury, wykorzystać ją do ilościowego opisywania procesów "twardych", czyli takich, które można traktować jak bezpośrednie zderzenia indywidualnych składników rozpraszanych na sobie dwu protonów. Dzięki temu QCD wraz z całym Modelem Standardowym stała się nieodzownym schematem teoretycznym używanym przy poszukiwaniu nowych cząstek i oddziaływań w akceleratorach takich jak LHC.