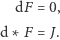Energia pola grawitacyjnego
Patrząc wstecz na rozwój podstawowych pojęć tworzących język, w którym współczesna fizyka opisuje otaczający nas świat, dostrzegamy ogromną rolę zasady zachowania energii...
Z pewną przesadą można byłoby powiedzieć, że każdy krok naprzód w tym odkrywaniu podstawowych praw fizyki polegał na:
- załamaniu się zasady zachowania, to znaczy na konstatacji, że gdzieś nam ta energia ucieka,
a potem na
- odkryciu całkiem nowego pola zjawisk i związanej z tym nowej formy energii.
I zawsze okazywało się, że energia nie gubi się, a jedynie zamienia się w nową, nie znaną nam dotychczas formę. Doskonałym przykładem na poparcie tej tezy było powstanie termodynamiki w początkach XIX wieku. Wtedy okazało się właśnie, że energia mechaniczna (kinetyczna + potencjalna) nie musi już być absolutnie zachowywana, bowiem może przekształcać się w energię wewnętrzną ("cieplną") ciał uczestniczących w opisywanych procesach fizycznych. A maszyny cieplne to przykład na transformację odwrotną: zamiany ciepła na pracę mechaniczną.
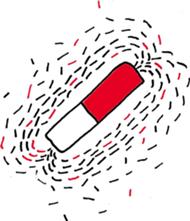
Prawie równolegle odbywała się druga wielka rewolucja w fizyce: od "mechanicznego" do "polowego" opisu oddziaływań. Jak pamiętamy ze szkoły, prawo powszechnego ciążenia sformułowane przez Newtona polegało na przypuszczeniu, że para dowolnych ciał przyciąga się z dobrze sprecyzowaną siłą, zależną od masy tych ciał i ich wzajemnej odległości. Myśląc np. o systemie planetarnym wokół Słońca, można było sobie wyobrażać, że między dowolnymi dwoma ciałami niebieskimi została rozpięta niewidzialna "sprężynka", realizująca to przyciąganie. Analogiczne "sprężynki" trzeba było sobie wyobrażać, by zrozumieć przyciąganie lub odpychanie ładunków elektrycznych opisane prawem Coulomba. Podobnie próbowano opisać oddziaływanie magnetyczne, ale tutaj sprawa okazała się bardziej skomplikowana. Tymczasem badania prowadzone przez Michaela Faradaya uświadamiały fizykom, że w celu zrozumienia istoty elektryczności i magnetyzmu warto porzucić mechanistyczne wyobrażenia "sprężynek". Zamiast tego Faraday wprowadził pojęcie "linii sił pola". Bardzo wyraźnie widać je, gdy rzucimy garść opiłków żelaznych na taflę szklaną, pod którą leży magnes. Opiłki układają się właśnie wzdłuż linii sił pola, które można wręcz fotografować. I choć nie umiemy równie spektakularnie wizualizować pola elektrycznego, to każdy zapewne widział w jakimś podręczniku rysunek reprezentujący ładunek elektryczny i wychodzące zeń koncentrycznie linie sił pola. Jeśli rysunek uwzględniał również drugi ładunek o przeciwnym znaku, to właśnie w nim zbiegały się te linie.
Zresztą same "linie pola" nie wnoszą tu nic istotnego. Ważne jest "pole", to znaczy jakaś własność samej przestrzeni otaczającej poruszające się ładunki (magnesy to też zamknięte obwody elektryczne, wytwarzające pole magnetyczne na mocy prawa Ampera!). Własność tę reprezentujemy za pomocą dwóch strzałek (wektorów): elektrycznego 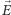 i magnetycznego
i magnetycznego 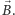 Gdy patrzymy nieuważnie na pusty z pozoru obszar przestrzeni, możemy przegapić ich istnienie. Jednak bardzo łatwo odkryć ich obecność, a nawet zmierzyć je dokładnie, gdy zaczniemy badać ruch malutkich (próbnych) ładunków w tym obszarze.
Gdy patrzymy nieuważnie na pusty z pozoru obszar przestrzeni, możemy przegapić ich istnienie. Jednak bardzo łatwo odkryć ich obecność, a nawet zmierzyć je dokładnie, gdy zaczniemy badać ruch malutkich (próbnych) ładunków w tym obszarze.
A zatem co się stanie, gdy pierwotnie obojętna elektrycznie kulka zostanie naładowana? No cóż, nie odbędzie się to bez jakiegoś nakładu pracy. Aby zgromadzić na takiej kulce ładunek elektryczny, można ją pocierać (vide piękny wiersz Juliana Tuwima "... o bursztynie, gdy się go pociera..."), można też użyć maszyny elektrostatycznej, albo też doprowadzić ładunek z jakiejś zewnętrznej baterii. W każdym razie proces ten wymaga, by z jakiegoś rezerwuaru energii (np. chemicznej, zmagazynowanej w naszych mięśniach) przeznaczyć jej trochę na ten cel. I co się teraz z tą energią stało? Czy została stracona? Otóż nie! Odnajdujemy ją właśnie w postaci energii pola elektrycznego i magnetycznego. Prawo zachowania energii zostanie ocalone, jeśli tylko zaakceptujemy jej nową formę: energię pola!!!
Mija właśnie 150 lat od czasu, gdy Maxwell opublikował ostateczną wersję elektrodynamiki, w której zaproponował równania rządzące dynamiką pól: elektrycznego i magnetycznego. Ich niezwykle złożona postać została znacznie uproszczona przez genialnego samouka Olivera Heaviside'a. Następnym krokiem była szczególna teoria względności Einsteina. Wykazał on, że pole elektryczne 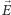 i magnetyczne
i magnetyczne 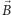 są jedynie subiektywnymi, zależnymi od obserwatora, emanacjami czegoś większego, mianowicie pewnej struktury geometrycznej niezależnej od obserwatora, obecnie nazywanej "polem elektromagnetycznym". Można się pochwalić, że równania Maxwella, które w oryginalnej wersji zajmowały całe strony, możemy teraz zapisać za pomocą zaledwie 9 znaków.
są jedynie subiektywnymi, zależnymi od obserwatora, emanacjami czegoś większego, mianowicie pewnej struktury geometrycznej niezależnej od obserwatora, obecnie nazywanej "polem elektromagnetycznym". Można się pochwalić, że równania Maxwella, które w oryginalnej wersji zajmowały całe strony, możemy teraz zapisać za pomocą zaledwie 9 znaków.
Ale nie ma to żadnego znaczenia dla problemu energii pola, której gęstość w próżni wyraża się (w odpowiednich jednostkach) w postaci:

W trakcie ewolucji pola energia ta może się przemieszczać w przestrzeni (opisuje to tzw. wektor Poyntinga), a także wymieniać się z innymi jej formami, np. mechaniczną w silniku elektrycznym czy cieplną w grzałce.
W roku 1915 Emma Noether wykazała, że prawa zachowania w teorii pola wiążą się z symetriami teorii (praca zawierająca ten wynik została jednak opublikowana dopiero w 1918 roku). I tak zasada zachowania energii jest wyrazem niezmienniczości elektrodynamiki względem przesunięć w czasie. Mówiąc językiem potocznym, oznacza to, że każde doświadczenie z polem elektromagnetycznym, powtórzone po pewnym czasie w tych samych warunkach, da ten sam wynik.
Polowy punkt widzenia zwyciężył również w teorii grawitacji. Jak już zauważyliśmy, analogia między prawem Coulomba a newtonowskim prawem powszechnego ciążenia jest uderzająca. Podobnie jak w początkach elektrodynamiki, opisywano to pole za pomocą "potencjału grawitacyjnego" - skalarnej funkcji, której skala zmienności reprezentowałaby "natężenie pola grawitacyjnego". Ale, podobnie jak w elektrodynamice, taki opis wystarczał jedynie do opisu sytuacji statycznych, np. do opisu ruchu planet w statycznym polu grawitacyjnym wytworzonym przez Słońce. Natomiast zupełnie zawodził w sytuacji dynamicznej, np. gdy chcemy uwzględnić wpływ planet na ruch samego Słońca. W takiej sytuacji potencjał grawitacyjny opisany po newtonowsku byłby "przylepiony na sztywno" do Słońca. Oznaczałoby to, że informacja o tym, że Słońce nieco się przesunęło, dotarłaby do dowolnie odległej gwiazdy dowolnie szybko. Kłóci się to z podstawowym założeniem teorii względności, tzw. postulatem przyczynowości, w myśl którego żadne oddziaływanie nie może rozchodzić się z prędkością większą niż prędkość światła.
Podobny paradoks zaistniałby w opisie zjawisk elektrycznych, gdybyśmy zatrzymali się na równaniu Coulomba. Jednak paradoks ten znika, gdy tylko opuścimy domenę elektrostatyki. Matematycznie elektrostatyka jest po prostu teorią równania Poissona nałożonego na jedną funkcję - potencjał skalarny. Musimy przejść do pełnej teorii Maxwella (najlepiej w wersji Einsteina!), w której do opisu konfiguracji pola nie wystarcza tylko jedna funkcja. Natomiast w teorii grawitacji kontemplacja tego i innych paradoksów doprowadziła Einsteina do sformułowania chyba najpiękniejszej i precyzyjnie sprawdzonej teorii fizycznej, jaką jest ogólna teoria względności. Stulecie jej sformułowania obchodzimy właśnie w bieżącym roku. W teorii tej "pole grawitacyjne" opisuje się strukturą geometryczną czasoprzestrzeni, która nie jest już dana a priori "od stworzenia Świata", lecz stanowi dynamiczne pole, ewoluujące według tzw. równań Einsteina. W luźnej analogii do elektrodynamiki można powiedzieć, że "potencjały grawitacyjne" to po prostu struktura metryczna czasoprzestrzeni, zaś "siły grawitacyjne" to tzw. struktura powiązania (czy też z angielska koneksji). W niniejszym artykule nie będziemy rozważać tych subtelności matematycznych. Interesuje nas natomiast pojęcie energii pola grawitacyjnego. Czy i tu obowiązuje zasada zachowania? Czy np. przyciągające się, a zatem przyspieszające, ciała niebieskie, zwiększając swą energię kinetyczną, czerpią ją właśnie z rezerwuaru energii pola zmagazynowanej w jego początkowej konfiguracji? Czy istnieje prosty wzór na gęstość tej energii, analogiczny do wzoru

dla elektromagnetyzmu?
Uczeni spierali się przez lata, jak opisać energię pola grawitacyjnego w sposób zgodny z procedurą przedstawioną przez Noether. Rodzi się jednak dużo poważniejsza wątpliwość: czy w ogóle jest możliwe, by całkowita energia 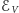 pola grawitacyjnego zmagazynowana w obszarze przestrzennym
pola grawitacyjnego zmagazynowana w obszarze przestrzennym 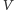 mogła mieć sensowne matematyczne własności. W szczególności, gdyby podzielić obszar
mogła mieć sensowne matematyczne własności. W szczególności, gdyby podzielić obszar 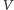 na dwie rozłączne części
na dwie rozłączne części 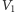 i
i 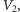 należałoby oczekiwać, że
należałoby oczekiwać, że

gdzie 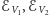 są energiami zgromadzonymi, odpowiednio, w obszarach
są energiami zgromadzonymi, odpowiednio, w obszarach 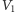 i
i 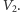
Taka własność energii pola grawitacyjnego kłóci się jednak z samą istotą grawitacji! Przecież już od pierwszych prac Einsteina w 1905 roku wiemy, że energia "waży", to znaczy ma masę! Słynny wzór 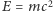 widział chyba każdy przedszkolak, choć jego popularyzatorzy popełniają zazwyczaj zasadniczy błąd, pisząc, że "masa może zmieniać się w energię". To nie tak! Masa jest energią. Wybuch bomby atomowej to nie zamiana masy na energię, lecz zamiana masy (energii) w inną jej postać. Współczynnik liczbowy
widział chyba każdy przedszkolak, choć jego popularyzatorzy popełniają zazwyczaj zasadniczy błąd, pisząc, że "masa może zmieniać się w energię". To nie tak! Masa jest energią. Wybuch bomby atomowej to nie zamiana masy na energię, lecz zamiana masy (energii) w inną jej postać. Współczynnik liczbowy 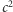 mówi jedynie o możliwości przeliczania różnych jednostek fizycznych, w których mierzymy tę samą wielkość. Na przykład w układzie SI, aby przeliczyć dżule
mówi jedynie o możliwości przeliczania różnych jednostek fizycznych, w których mierzymy tę samą wielkość. Na przykład w układzie SI, aby przeliczyć dżule 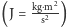 na "czyste" kilogramy, potrzebny jest przelicznik o mianie
na "czyste" kilogramy, potrzebny jest przelicznik o mianie 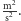 Einstein odkrył, że tym uniwersalnym przelicznikiem jest właśnie kwadrat prędkości światła
Einstein odkrył, że tym uniwersalnym przelicznikiem jest właśnie kwadrat prędkości światła 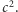 Tak więc w teorii grawitacji musimy pogodzić się z faktem, że w obszarze
Tak więc w teorii grawitacji musimy pogodzić się z faktem, że w obszarze 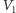 zmagazynowana została masa
zmagazynowana została masa 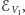 a w obszarze
a w obszarze 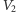 zmagazynowana została masa
zmagazynowana została masa 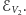 Czytelnik o konserwatywnych poglądach, który nie lubi mierzyć masy w dżulach, może na swój użytek przeliczać to wszystko na kilogramy, dzieląc nasze wzory przez
Czytelnik o konserwatywnych poglądach, który nie lubi mierzyć masy w dżulach, może na swój użytek przeliczać to wszystko na kilogramy, dzieląc nasze wzory przez 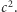 (Tego rodzaju fobie można porównać do problemu turysty podróżującego samochodem między USA a Kanadą, który nie śmie zapisać wzoru na całkowitą drogę w postaci
(Tego rodzaju fobie można porównać do problemu turysty podróżującego samochodem między USA a Kanadą, który nie śmie zapisać wzoru na całkowitą drogę w postaci 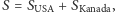 bo przecież
bo przecież 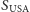 mierzy się w milach, a
mierzy się w milach, a 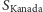 już w kilometrach!) Ale grawitacja to prawo powszechnego ciążenia, w myśl którego każde dwie masy przyciągają się. Zatem całkowita energia (masa) pola zmagazynowana w
już w kilometrach!) Ale grawitacja to prawo powszechnego ciążenia, w myśl którego każde dwie masy przyciągają się. Zatem całkowita energia (masa) pola zmagazynowana w 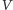 nie może być sumą energii (mas) zmagazynowanych w
nie może być sumą energii (mas) zmagazynowanych w 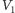 i
i 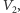 bowiem musi zostać pomniejszona o energię ich oddziaływania, jakim jest to przyciąganie. A zatem wiemy na pewno, że energia nie może być addytywna, czyli inaczej niż w teoriach pola opartych na twierdzeniu Noether, w grawitacji musi zachodzić nierówność:
bowiem musi zostać pomniejszona o energię ich oddziaływania, jakim jest to przyciąganie. A zatem wiemy na pewno, że energia nie może być addytywna, czyli inaczej niż w teoriach pola opartych na twierdzeniu Noether, w grawitacji musi zachodzić nierówność:

Ten paradoks stanowi poważne wyzwanie dla fizyków i matematyków zajmujących się ogólną teorią względności. Nie możemy tutaj wgłębiać się bardziej w jego istotę, bo do tego potrzebny jest zaawansowany aparat matematyczny. Warto natomiast podkreślić, że inaczej niż chociażby w elektrodynamice, w teorii względności nie dysponujemy pojęciem gęstości energii pola, bo energia pola w danym obszarze nie jest sumą wkładów energii od jego części. Energia jest wielkością nielokalną. Okazuje się jednak, że nie ma wątpliwości co do tego, jak opisywać całkowitą energię (masę) izolowanego układu pól i mas, to znaczy takiego, że poza jakimś ograniczonym obszarem przestrzeń nie zawiera żadnych mas. Tę całkowitą energię opisuje wielkość geometryczna zwana "masą ADM" od nazwisk badaczy, którzy ją zaproponowali w słynnym artykule opublikowanym w 1962 roku: R. Arnowitt, S. Deser oraz C. W. Misner. Natomiast próby opisania energii grawitacyjnej zawartej nie w całej przestrzeni, a jedynie w jej ograniczonym kawałku, polegają najczęściej na tzw. konstrukcjach quasilokalnych i wiążą się m.in. z nazwiskiem Rogera Penrose'a. Również w Warszawie prowadzone są badania takich struktur.