Nowe pomysły
Wszechświat w łazience
Małą łazienkę można, zdaniem architektów, optycznie powiększyć, montując w niej duże lustro. W miejscach mniej ograniczonych wymaganiami funkcjonalności, takich jak toalety muzeów sztuki nowoczesnej czy klatki schodowe centrów handlowych, umieszcza się niekiedy lustra na przeciwnych ścianach, co daje złudzenie nieskończonej głębi w kierunkach prostopadłych do luster...
Nie jest wykluczone, że podobne rozumowanie możemy zastosować również do całego Wszechświata. Może po prostu wydaje nam się „nieskończony” dzięki właściwie ustawionym odpowiednikom luster. Oczywiście, „lustra” te nie mogą być obiektami fizycznymi. Niemal taki sam efekt możemy jednak uzyskać, odpowiednio utożsamiając punkty brzegowe pewnej skończonej komórki przestrzeni.

Rys. 1
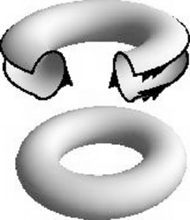
Rys. 2
Rozważmy na początek znacznie prostszy przypadek przestrzeni dwuwymiarowej, konkretnie kwadratu, którego brzegi skleimy zgodnie z kierunkiem strzałek, tak jak na rysunku 1. Otrzymamy wówczas powierzchnię przedstawioną na rysunku 2, czyli torus – oczywiście w sensie topologicznym, tzn. z dokładnością do ciągłego i różnowartościowego przekształcenia, które możemy sobie wyobrażać jako rozciąganie i przesuwanie (bez rozrywania!) rozważanego obiektu, wykonanego z elastycznego materiału. Materiał posklejanego kwadratu nie jest jednak rozciągany, w związku z tym w okolicy każdego miejsca (również na sklejeniu) jest w dalszym ciągu kawałkiem zwykłej płaszczyzny. Ma zatem torus ważną cechę wspólną z ulubionym przez kosmologów modelem Wszechświata: jest taki sam oglądany z dowolnego punktu (jednorodny) i dowolnego kierunku (izotropowy).
Pomimo tego, że torus powstał ze skończonej komórki, daje on nam wrażenie „nieskończoności” przestrzeni. Jeżeli z ustalonego punktu torusa wysłać rozchodzący się po nim wzdłuż linii prostej sygnał, to będzie się on przemieszczał, nie napotykając nigdy krańca tego obiektu. Ignorujemy tu subtelne rozważania, czym jest prosta na torusie, i mamy na myśli proste w kwadracie z rysunku 1.
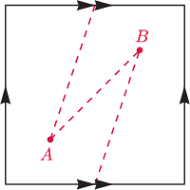
Rys. 3
Co ciekawe, istnieje więcej niż jedna droga, jaką może podróżować sygnał
wysłany z punktu
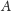 do punktu
do punktu
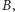 co pokazano na rysunku 3.
Jeżeli w punkcie
co pokazano na rysunku 3.
Jeżeli w punkcie
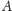 znajduje się źródło światła, a w punkcie
znajduje się źródło światła, a w punkcie
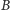 – obserwator, stwierdzi on, że światło z tego samego źródła dociera do niego
z różnych kierunków przestrzeni. Oznacza to, że obserwator będzie widział
wiele obrazów tego samego źródła (Czytelnik, po namyśle, zauważy, że
w tym przykładzie obrazów będzie nieskończenie wiele, choć w różnych
odległościach!).
– obserwator, stwierdzi on, że światło z tego samego źródła dociera do niego
z różnych kierunków przestrzeni. Oznacza to, że obserwator będzie widział
wiele obrazów tego samego źródła (Czytelnik, po namyśle, zauważy, że
w tym przykładzie obrazów będzie nieskończenie wiele, choć w różnych
odległościach!).
W podobny sposób zamiast torusa możemy uzyskać butelkę Kleina, a prościej – przez sklejenie tylko jednej pary boków – walec czy wstęgę Möbiusa.
Gdybyśmy jednak chcieli uzyskać inne powierzchnie, np. sferę, bez rozciągania już by się nie obeszło. Ale i w tym przypadku można by to zrobić tak, aby otrzymana przestrzeń była jednorodna i izotropowa.
Mówiąc uczenie, w opisanych dotąd przykładach zmienialiśmy globalne własności przestrzeni, czyli to, jak wygląda rozważana przestrzeń jako całość. Jeśliby wykonać podobne ćwiczenie w trzech wymiarach, moglibyśmy uzyskać różne kształty Wszechświata. Równania opisujące dynamikę (czaso)przestrzeni mają bowiem charakter lokalny, tj. zmiana parametrów opisujących dany punkt Wszechświata zależy jedynie od wartości tych parametrów w bardzo małym otoczeniu rozważanego punktu, a nie od kształtu przestrzeni jako całości.
Ktoś mógłby się tu żachnąć, że przedstawiona konstrukcja nie ma wiele wspólnego z Wszechświatem, w którym nie widzimy przecież wielokrotnych obrazów tych samych ciał niebieskich (jeśli pominąć znajdujące się bardzo blisko na sferze niebieskiej wielokrotne obrazy z soczewkowania grawitacyjnego, to jest jednak zupełnie inne zagadnienie). Co jednak, jeśli rozmiar obserwowanego Wszechświata jest porównywalny z rozmiarem podstawowej komórki? Czy można jakoś wykryć, że Wszechświat jest „uszyty” ze skończonego kawałka przestrzeni?
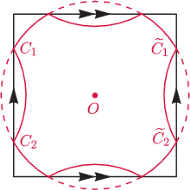
Rys. 4
Okazuje się, że w zasadzie można. Dociera do nas bowiem tzw. mikrofalowe
promieniowanie tła, wysłane mniej więcej 300 tysięcy lat po Wielkim Wybuchu,
kiedy swobodne wcześniej jądra atomowe i elektrony połączyły się w atomy.
Promieniowanie to zostało wyemitowane w zasadzie równocześnie w całej
objętości przestrzeni; to widziane dzisiaj pochodzi zatem z powierzchni sfery,
którą w naszym modelu dwuwymiarowego torusa możemy przedstawić tak
jak na rysunku 4. Linią ciągłą zaznaczono zbiór takich punktów podstawowej
komórki, że wyemitowane z nich światło dociera do obserwatora
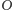 w tym samym ustalonym czasie. Niektóre fragmenty tej figury wydają
się bliższe obserwatora
w tym samym ustalonym czasie. Niektóre fragmenty tej figury wydają
się bliższe obserwatora
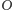 niż inne: światło wysłane z nich najkrótszą
drogą minęło go już dawno temu i obecnie widzi on promienie biegnące drogą
„okrężną”. Linią przerywaną zaznaczono położenia, jakie obserwator
niż inne: światło wysłane z nich najkrótszą
drogą minęło go już dawno temu i obecnie widzi on promienie biegnące drogą
„okrężną”. Linią przerywaną zaznaczono położenia, jakie obserwator
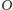 przypisałby obrazom tych fragmentów, nie wiedząc, że podstawowa
komórka przestrzeni jest skończona.
przypisałby obrazom tych fragmentów, nie wiedząc, że podstawowa
komórka przestrzeni jest skończona.

NASA/WMAP Science Team
Rys. 5 Mapa fluktuacji mikrofalowego promieniowania tła zmierzonych przez satelitę WMAP. Jaśniejsze (ciemniejsze) punkty odpowiadają dodatnim (ujemnym) fluktuacjom natężenia.
Mikrofalowe promieniowanie tła jest niemal izotropowe, zawiera jednak maleńkie fluktuacje natężenia, które pozwalają odróżnić różne kierunki na sferze niebieskiej.
W naszym przykładzie torusa fluktuacje zmierzone w punktach
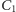 i
i
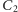 na rysunku 4 powinny być takie same jak te zmierzone
w punktach odpowiednio
na rysunku 4 powinny być takie same jak te zmierzone
w punktach odpowiednio
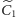 i
i
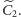 Jeśli rozważalibyśmy
przykład trójwymiarowy i np. utożsamili przeciwległe ściany sześcianu,
zamiast par punktów mielibyśmy znajdujące się po przeciwnych stronach sfery
niebieskiej okręgi. Wzdłuż tych okręgów fluktuacje mikrofalowego
promieniowania tła powinny być dokładnie takie same. Nie pozostaje zatem
chyba nic innego jak poszukać takich okręgów w mapach mikrofalowego
promieniowania tła.
Jeśli rozważalibyśmy
przykład trójwymiarowy i np. utożsamili przeciwległe ściany sześcianu,
zamiast par punktów mielibyśmy znajdujące się po przeciwnych stronach sfery
niebieskiej okręgi. Wzdłuż tych okręgów fluktuacje mikrofalowego
promieniowania tła powinny być dokładnie takie same. Nie pozostaje zatem
chyba nic innego jak poszukać takich okręgów w mapach mikrofalowego
promieniowania tła.
Zanim jednak zabierzemy się do pracy, pamiętajmy, że przytoczone tu przykłady dwu- i trójwymiarowego torusa to zaledwie najprostsze do wyobrażenia możliwości. Ile jest wszystkich i jak wyglądają? Próba odpowiedzi na pierwsze z tych pytań to wykraczająca znacznie poza ramy tego artykułu wyprawa w krainę matematyki. Narzędzi do klasyfikacji przestrzeni trójwymiarowych dostarcza udowodniona przez Perelmana hipoteza geometryzacyjna Thurstona, o której pisze Zdzisław Pogoda. Nawet jeśli chcemy ograniczyć nasze rozważania do przestrzeni jednorodnych i izotropowych, i tak pozostaje mnóstwo możliwości.
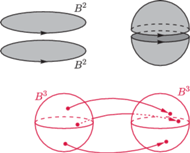
Rys. 6 Zwykłą dwuwymiarową sferę możemy otrzymać, sklejając odpowiednio brzegi dwóch kół. Sfera trójwymiarowa powstaje przez sklejenie brzegów dwóch kul.

Rys. 7 Dwunastościan sferyczny

Rys. 8
Kosmologowie zbadali dokładniej pewien interesujący przypadek możliwego kształtu Wszechświata. Opisuje on przestrzeń zakrzywioną, której najprostszą realizacją jest trójwymiarowa sfera. Już to jest trudne do wyobrażenia, gdyż u większości ludzi geometryczne intuicje dobrze działają tylko dla obiektów dających się zanurzyć w trzech wymiarach. Tymczasem realizację trójwymiarowej sfery możemy otrzymać dzięki odpowiedniemu sklejeniu brzegów dwóch kul, przedstawionemu na rysunku 6, której to operacji w trzech wymiarach wykonać się nie da.
Podobnie jak torus „udawał” nieskończoną trójwymiarową przestrzeń,
także trójwymiarowa sfera może być iluzją zbudowaną z mniejszych
komórek. Jedną z takich konstrukcji, podaną po raz pierwszy przez
Poincarégo, otrzymuje się w następujący sposób. Zaczynamy od podstawowej
komórki będącej sferycznym dwunastościanem foremnym, przedstawionym
na rysunku 7. Każdą ze ścian tego dwunastościanu utożsamiamy
ze ścianą przeciwległą obróconą o kąt
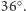 Utożsamienie to
prowadzi znowu do wrażenia „nieskończonej” przestrzeni. Jeśliby dla
lepszej wizualizacji pozostawić krawędzie dwunastościanu jako swego
rodzaju rusztowanie w tej przestrzeni, to wyglądałaby ona tak jak na
rysunku 8.
Utożsamienie to
prowadzi znowu do wrażenia „nieskończonej” przestrzeni. Jeśliby dla
lepszej wizualizacji pozostawić krawędzie dwunastościanu jako swego
rodzaju rusztowanie w tej przestrzeni, to wyglądałaby ona tak jak na
rysunku 8.
Okazuje się, że Wszechświat zbudowany z takich komórek miałby pewne korzystne własności. W tradycyjnych modelach kosmologicznych, używających prawdziwej nieskończonej przestrzeni, fluktuacje mikrofalowego promieniowania tła dla największych widzialnych na niebie skal kątowych są znacznie mniejsze niż wynikające z rozsądnych założeń przewidywania teoretyczne. Problem ten nie występuje dla Wszechświata zbudowanego z opisanych tu trójwymiarowych rozmaitości, między innymi z uwagi na występowanie maksymalnej długości fali tych fluktuacji, która może być nieco mniejsza niż największe skale odległości obserwowalne w mikrofalowym promieniowaniu tła. Model ten bywa jednak krytykowany z uwagi na to, że wymaga Wszechświata o niewielkiej dodatniej krzywiźnie, co trudno jest pogodzić z postulatem, że fluktuacje mikrofalowego promieniowania tła powstały podczas inflacji, która „spłaszczyła” przestrzeń do tego stopnia, że jej ewentualna krzywizna nie powinna być możliwa do zaobserwowania. Rozstrzygnięcie tego sporu na niekorzyść modelu tradycyjnego wymagałoby potwierdzenia obecności fluktuacji powtarzających się systematycznie wzdłuż odpowiednich okręgów. Mimo podejmowanych przez różne zespoły badawcze prób sytuacja wciąż jeszcze jest niejasna. Pozostaje mieć nadzieję, że spodziewane w tym roku nowe dane z satelity Planck pomogą w wyjaśnieniu tej zagadki.