Co to jest?
Mała Delta
Ziomkowie i Wszechświat
Wyobraźmy sobie małe, senne miasteczko na rubieży kresów, zamieszkane
przez
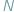 osób...
osób...
Wszystkie te osoby się znają, mieszkają tutaj przecież od zawsze. W niedzielne
popołudnie wszyscy wychodzą na rynek i przechadzają się. Ludzie ci są
nieskomplikowani, każdy może być w jednym z dwóch stanów
psychicznych, tj. albo wesoły (takich będziemy oznaczać przez
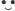 , a ich
liczbę przez
, a ich
liczbę przez
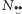 ), albo smutny (na tych dobrym oznaczeniem będą
odpowiednio
), albo smutny (na tych dobrym oznaczeniem będą
odpowiednio
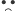 i
i
 ). Prawa rządzące psychiką naszych
bohaterów nie są nazbyt złożone, a każdy na pewno zna je z codziennych,
chcianych czy nie, doświadczeń. Kiedy osobnik wesoły spotyka innego
wesołego, w wyniku nagłej i niepowstrzymanej zazdrości smutnieje, zatem
zachodzi proces, który schematycznie możemy zapisać jako:
). Prawa rządzące psychiką naszych
bohaterów nie są nazbyt złożone, a każdy na pewno zna je z codziennych,
chcianych czy nie, doświadczeń. Kiedy osobnik wesoły spotyka innego
wesołego, w wyniku nagłej i niepowstrzymanej zazdrości smutnieje, zatem
zachodzi proces, który schematycznie możemy zapisać jako:

Kiedy człowiek smutny spotyka innego smutnego, w wyniku reakcji określanej z niemiecka jako Schadenfreude, czyli radość z cudzego nieszczęścia, momentalnie weseleje:

Nikogo pewnie nie zdziwi wiadomość, że przy spotkaniu człowieka wesołego ze smutnym żaden z nich nie zmieni swego stanu. Dodajmy jeszcze, że kontakty społeczne są raczej powierzchowne, toteż nie zdarzają się spotkania aż trzech lub więcej osób naraz, a szlak spaceru po rynku wynika raczej z przypadkowych kaprysów niż jakichś konkretnych, ustalonych przed wyjściem z domu planów. Co można powiedzieć o zmianach liczby wesołych i smutnych obywateli?
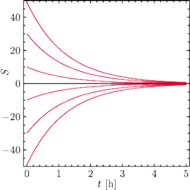
Rys. 1 Ewolucja czasowa szczęścia
 opisywanego wzorem (1) dla różnych wartości
opisywanego wzorem (1) dla różnych wartości
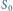 przy stałej
przy stałej
 równej 0,25/min oraz
równej 0,25/min oraz
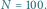
Prawdopodobieństwo tego, że człowiek wesoły posmutnieje w wyniku napotkania
innego wesołego w ciągu ustalonego przedziału czasowego
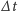 , jest
proporcjonalne do liczby innych wesołych, zatem
, jest
proporcjonalne do liczby innych wesołych, zatem

gdzie
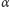 jest ustalonym współczynnikiem proporcjonalności. Podobnie,
prawdopodobieństwo poweselenia smutnego możemy napisać jako
jest ustalonym współczynnikiem proporcjonalności. Podobnie,
prawdopodobieństwo poweselenia smutnego możemy napisać jako
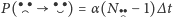 . Jeżeli zaś całkowitym szczęściem
społeczeństwa nazwiemy różnicę między liczbą obywateli wesołych
i smutnych, to zmianę szczęścia możemy oszacować przez
. Jeżeli zaś całkowitym szczęściem
społeczeństwa nazwiemy różnicę między liczbą obywateli wesołych
i smutnych, to zmianę szczęścia możemy oszacować przez

gdzie czynnik
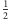 zapobiega policzeniu każdego spotkania dwóch osób
dwukrotnie, natomiast czynnik 4 uwzględnia zmianę szczęścia o 4 jednostki
przy spotkaniu zmieniającym stany psychiczne. Podstawiając obliczone
uprzednio prawdopodobieństwa i zakładając, że liczba osób jest na tyle
duża, że możemy zaniedbać odejmowanie jedynki w tych wynikach,
otrzymujemy:
zapobiega policzeniu każdego spotkania dwóch osób
dwukrotnie, natomiast czynnik 4 uwzględnia zmianę szczęścia o 4 jednostki
przy spotkaniu zmieniającym stany psychiczne. Podstawiając obliczone
uprzednio prawdopodobieństwa i zakładając, że liczba osób jest na tyle
duża, że możemy zaniedbać odejmowanie jedynki w tych wynikach,
otrzymujemy:

Zatem zmiana wielkości
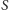 w jednostce czasu jest wprost proporcjonalna
do tej wielkości, co oznacza, że całkowite szczęście jest opisywane funkcją
wykładniczą:
w jednostce czasu jest wprost proporcjonalna
do tej wielkości, co oznacza, że całkowite szczęście jest opisywane funkcją
wykładniczą:
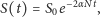 | (1) |
gdzie
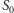 jest wartością początkową szczęścia. Wykres takiej funkcji dla
różnych warunków początkowych pokazany jest na rysunku 1. Niezależnie
od początkowego szczęścia miasteczka po upływie niezbyt długiego czasu
całkowite szczęście osiąga, niestety, wartość bliską zeru.
jest wartością początkową szczęścia. Wykres takiej funkcji dla
różnych warunków początkowych pokazany jest na rysunku 1. Niezależnie
od początkowego szczęścia miasteczka po upływie niezbyt długiego czasu
całkowite szczęście osiąga, niestety, wartość bliską zeru.
W sąsiednim miasteczku panują trochę inne zwyczaje. Procesy psychiczne u ludzi przebiegają, oczywiście, tak samo, ale w niedzielne popołudnia mieszkańcy nie spacerują po rynku, tylko wybierają się na długie wędrówki po okolicznych lasach i łąkach, tak że zajmowany przez nich teren powiększa się w miarę upływu czasu, aż do zapadnięcia zmierzchu, kiedy to wszyscy samotnie wracają do domu. Jak zmienia się całkowite szczęście owego miasteczka?
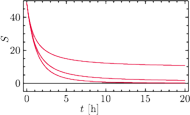
Rys. 2 Ewolucja czasowa szczęścia
 z funkcją
z funkcją
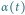 opisywaną wzorem (2) dla
różnych wartości
opisywaną wzorem (2) dla
różnych wartości
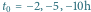 (od góry do dołu) przy
(od góry do dołu) przy
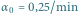 ,
,
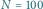 oraz
oraz
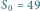 .
.
Zanim postaramy się to opisać mądrym wzorem, zastanówmy się, czym
różni się dynamika spotkań międzyludzkich w obu miasteczkach. Nietrudno
zauważyć, że w pierwszym obywatele zajmują stałą powierzchnię,
podczas gdy w drugim powierzchnia ta się powiększa, a co za tym idzie,
prawdopodobieństwo spotkania maleje. W pewnej chwili może ono
osiągnąć wartość tak małą, że żadne dwie osoby nie spotkają się
już przed wieczornym powrotem do domu – a wartość szczęścia
przestanie się w praktyce zmieniać, osiągając pewną niezerową wartość.
W naszym prostym modelu odpowiada to przyjęciu malejącego z czasem
współczynnika
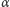 . Dla pewnego szczególnego wyboru
. Dla pewnego szczególnego wyboru
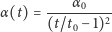 | (2) |
otrzymujemy rozwiązania przedstawione na rysunku 2.
Gdzie szukać takich miasteczek, chciałby pewnie wiedzieć Czytelnik Lubiący Konkrety. Czas przyznać się, że opowiadanie tu przedstawione jest po prostu metaforą: drugim miasteczkiem jest wczesny Wszechświat, ludzie weseli i smutni to określony rodzaj cząstek i antycząstek, oddziaływania polegają zaś na zamianie par cząstek w pary antycząstek, natomiast ustalone szczęście odpowiada ustalonej liczbie cząstek i antycząstek w pewnym obszarze Wszechświata. Co prawda, znane cząstki nie mają aż tak prostych oddziaływań, ale nie jest trudno poprawić taki model, by uwzględniał np. procesy anihilacji danego rodzaju cząstek i antycząstek w jakieś inne cząstki, które z powodu zachowania energii nie będą już mogły wytworzyć wyjściowej pary...
Czemu rozmyślać o takich rzeczach? Według obecnej wiedzy istnienie materii, z której jesteśmy zbudowani, oraz ciemnej materii wypełniającej Wszechświat wiąże się z ustaniem oddziaływań zmieniających liczbę tych cząstek w pewnych momentach ewolucji Wszechświata. Nieznane pozostaje wszakże wiele konkretnych szczegółów...
 opisywanego wzorem (1) dla różnych wartości
opisywanego wzorem (1) dla różnych wartości
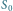 przy stałej
przy stałej
 równej 0,25/min oraz
równej 0,25/min oraz
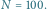
 z funkcją
z funkcją
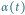 opisywaną wzorem (2) dla
różnych wartości
opisywaną wzorem (2) dla
różnych wartości
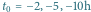 (od góry do dołu) przy
(od góry do dołu) przy
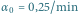 ,
,
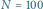 oraz
oraz
 .
.