Niech 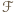 będzie rodziną
będzie rodziną  podzbiorów zbioru
podzbiorów zbioru 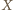 , spełniającą zadane warunki. Jeżeli do
, spełniającą zadane warunki. Jeżeli do 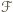 należy zbiór pusty lub zbiór pełny (cały zbiór
należy zbiór pusty lub zbiór pełny (cały zbiór 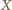 ), to już żaden inny zbiór nie może do
), to już żaden inny zbiór nie może do 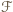 należeć. W tym przypadku
należeć. W tym przypadku 
Jeżeli do 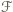 należy pewien zbiór jednoelementowy
należy pewien zbiór jednoelementowy 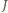 oraz pewien zbiór
oraz pewien zbiór 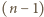 -elementowy
-elementowy 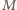 , to muszą się one dopełniać (bo inaczej
, to muszą się one dopełniać (bo inaczej 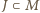 ) oraz żaden inny zbiór nie może do
) oraz żaden inny zbiór nie może do 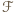 należeć (bo albo zawiera
należeć (bo albo zawiera 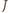 , albo jest zawarty w
, albo jest zawarty w 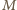 ). W tym przypadku
). W tym przypadku 
Przyjmijmy dalej, że żadna z tych sytuacji nie ma miejsca. Wszystkie zbiory w 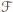 mają z założenia różne liczności. Wykluczone zostały liczności
mają z założenia różne liczności. Wykluczone zostały liczności 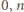 oraz albo
oraz albo 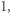 albo
albo 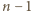 . Pozostaje
. Pozostaje 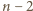 możliwych liczności. Zatem
możliwych liczności. Zatem 
Pokażemy teraz, że dla każdego 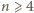 istnieje w zbiorze
istnieje w zbiorze 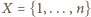 rodzina
rodzina 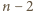 podzbiorów
podzbiorów 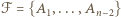 o wymaganych własnościach. Najpierw przykłady dla
o wymaganych własnościach. Najpierw przykłady dla 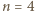 ,
, 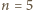 :
:
Dalej indukcja ze skokiem o 2. Niech 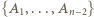 będzie "dobrą" rodziną podzbiorów zbioru
będzie "dobrą" rodziną podzbiorów zbioru 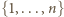 , ponumerowanych tak, że
, ponumerowanych tak, że 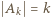 dla
dla 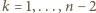 . Bierzemy zbiór
. Bierzemy zbiór 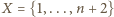 i określamy:
i określamy:
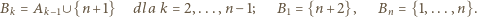
Widać, że 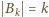 dla
dla 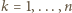 i że żaden ze zbiorów
i że żaden ze zbiorów 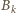 nie jest podzbiorem innego. Tak więc
nie jest podzbiorem innego. Tak więc 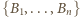 jest rodziną podzbiorów
jest rodziną podzbiorów 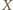 , o jaką chodzi.
, o jaką chodzi.
Dostajemy odpowiedź: dla każdej liczby 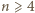 maksymalna liczność rodziny
maksymalna liczność rodziny 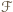 wynosi
wynosi 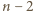 .
.
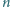 pytań (
pytań (
 ). Pewna liczba studentów
przystąpiła do tego egzaminu. Wiadomo, że dla każdych dwóch studentów
było przynajmniej jedno pytanie, na które obaj znali odpowiedź, ale dla
żadnej pary studentów nie było tak, że obaj znali odpowiedzi na dokładnie
te same pytania. Udowodnić, że do egzaminu przystąpiło co najwyżej
). Pewna liczba studentów
przystąpiła do tego egzaminu. Wiadomo, że dla każdych dwóch studentów
było przynajmniej jedno pytanie, na które obaj znali odpowiedź, ale dla
żadnej pary studentów nie było tak, że obaj znali odpowiedzi na dokładnie
te same pytania. Udowodnić, że do egzaminu przystąpiło co najwyżej
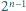 studentów.
studentów.
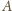 zbioru
zbioru
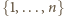 łączymy w nieuporządkowane pary
postaci
łączymy w nieuporządkowane pary
postaci
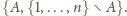 Takich par jest
Takich par jest
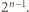 Wobec założenia
z treści zadania każdego studenta możemy utożsamiać jednoznacznie ze
zbiorem pytań, na które zna odpowiedź. Gdyby studentów było więcej niż
Wobec założenia
z treści zadania każdego studenta możemy utożsamiać jednoznacznie ze
zbiorem pytań, na które zna odpowiedź. Gdyby studentów było więcej niż
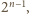 to znalazłoby się dwóch, którym odpowiadałyby zbiory
to znalazłoby się dwóch, którym odpowiadałyby zbiory
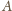 i
i
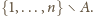 To jednak przeczyłoby założeniu, że na egzaminie było
pytanie, na które obaj znali odpowiedź.
To jednak przeczyłoby założeniu, że na egzaminie było
pytanie, na które obaj znali odpowiedź.
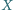 będzie zbiorem
będzie zbiorem  -elementowym (
-elementowym ( 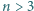 ). Wyznaczyć największą liczbę
). Wyznaczyć największą liczbę 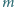 , dla której w zbiorze
, dla której w zbiorze 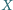 istnieje
istnieje  podzbiorów, z których żaden nie zawiera się w innym oraz żaden nie jest równoliczny z innym.
podzbiorów, z których żaden nie zawiera się w innym oraz żaden nie jest równoliczny z innym.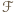 będzie rodziną
będzie rodziną  podzbiorów zbioru
podzbiorów zbioru 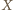 , spełniającą zadane warunki. Jeżeli do
, spełniającą zadane warunki. Jeżeli do 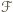 należy zbiór pusty lub zbiór pełny (cały zbiór
należy zbiór pusty lub zbiór pełny (cały zbiór 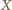 ), to już żaden inny zbiór nie może do
), to już żaden inny zbiór nie może do 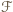 należeć. W tym przypadku
należeć. W tym przypadku 
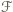 należy pewien zbiór jednoelementowy
należy pewien zbiór jednoelementowy 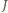 oraz pewien zbiór
oraz pewien zbiór 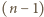 -elementowy
-elementowy 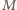 , to muszą się one dopełniać (bo inaczej
, to muszą się one dopełniać (bo inaczej 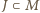 ) oraz żaden inny zbiór nie może do
) oraz żaden inny zbiór nie może do 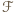 należeć (bo albo zawiera
należeć (bo albo zawiera 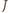 , albo jest zawarty w
, albo jest zawarty w 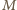 ). W tym przypadku
). W tym przypadku 
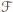 mają z założenia różne liczności. Wykluczone zostały liczności
mają z założenia różne liczności. Wykluczone zostały liczności 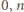 oraz albo
oraz albo 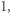 albo
albo 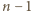 . Pozostaje
. Pozostaje 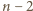 możliwych liczności. Zatem
możliwych liczności. Zatem 
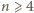 istnieje w zbiorze
istnieje w zbiorze 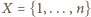 rodzina
rodzina 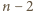 podzbiorów
podzbiorów 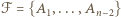 o wymaganych własnościach. Najpierw przykłady dla
o wymaganych własnościach. Najpierw przykłady dla 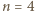 ,
, 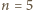 :
: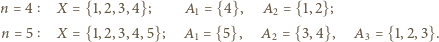
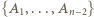 będzie "dobrą" rodziną podzbiorów zbioru
będzie "dobrą" rodziną podzbiorów zbioru 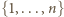 , ponumerowanych tak, że
, ponumerowanych tak, że 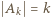 dla
dla 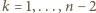 . Bierzemy zbiór
. Bierzemy zbiór 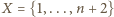 i określamy:
i określamy: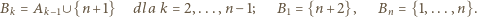
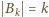 dla
dla 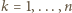 i że żaden ze zbiorów
i że żaden ze zbiorów 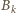 nie jest podzbiorem innego. Tak więc
nie jest podzbiorem innego. Tak więc 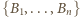 jest rodziną podzbiorów
jest rodziną podzbiorów 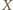 , o jaką chodzi.
, o jaką chodzi.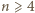 maksymalna liczność rodziny
maksymalna liczność rodziny 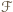 wynosi
wynosi 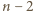 .
.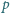 będzie liczbą pierwszą postaci
będzie liczbą pierwszą postaci
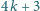 . Dowieść, że
zbioru złożonego z
. Dowieść, że
zbioru złożonego z
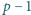 kolejnych liczb całkowitych nie da się
podzielić na dwa podzbiory w taki sposób, aby iloczyn liczb w jednym
podzbiorze był równy iloczynowi liczb w drugim podzbiorze.
kolejnych liczb całkowitych nie da się
podzielić na dwa podzbiory w taki sposób, aby iloczyn liczb w jednym
podzbiorze był równy iloczynowi liczb w drugim podzbiorze.
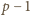 kolejnych liczb całkowitych jest liczba podzielna
przez
kolejnych liczb całkowitych jest liczba podzielna
przez
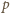 , to iloczyn liczb w jednym podzbiorze jest podzielny przez
, to iloczyn liczb w jednym podzbiorze jest podzielny przez
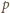 ,
a iloczyn w drugim nie jest podzielny przez
,
a iloczyn w drugim nie jest podzielny przez
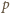 . Możemy więc przyjąć,
że wśród
. Możemy więc przyjąć,
że wśród
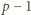 kolejnych liczb całkowitych nie ma liczby podzielnej
przez
kolejnych liczb całkowitych nie ma liczby podzielnej
przez
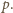
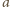 iloczyn liczb w jednym podzbiorze, a przez
iloczyn liczb w jednym podzbiorze, a przez
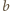 iloczyn liczb w drugim i przyjmijmy, że
iloczyn liczb w drugim i przyjmijmy, że
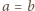 . Wówczas, na mocy
twierdzenia Wilsona,
. Wówczas, na mocy
twierdzenia Wilsona,
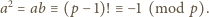
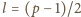 jest nieparzysta, więc
jest nieparzysta, więc
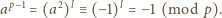
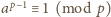 . Otrzymaliśmy sprzeczność, która dowodzi, że
. Otrzymaliśmy sprzeczność, która dowodzi, że
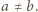
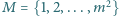 , gdzie
, gdzie
 jest ustaloną liczbą naturalną.
jest ustaloną liczbą naturalną.
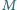 podzbiorów niezawierających pary liczb,
których różnica dzieli się przez
podzbiorów niezawierających pary liczb,
których różnica dzieli się przez
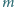 ?
?
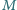 podzbiorów niezawierających pary liczb,
których różnica jest
równa
podzbiorów niezawierających pary liczb,
których różnica jest
równa
 ?
?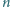 -elementowy zbiór
-elementowy zbiór
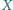
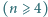 oraz
oraz
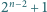 jego podzbiorów. Wykazać, że wśród tych podzbiorów
istnieją takie cztery, których część wspólna jest zbiorem pustym lub
jednoelementowym.
jego podzbiorów. Wykazać, że wśród tych podzbiorów
istnieją takie cztery, których część wspólna jest zbiorem pustym lub
jednoelementowym.