Dyskretny Darboux»Zadanie 6
o zadaniu...
- Zadanie pochodzi z artykułu Dyskretny Darboux
- Publikacja w Delcie: maj 2020
- Publikacja elektroniczna: 30 kwietnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (365 KB)
Dany jest wielokąt wypukły o parzystej liczbie boków. Każdy bok wielokąta ma długość 2 lub 3, przy czym liczba boków każdej z tych długości jest parzysta. Dowieść, że istnieją dwa wierzchołki wielokąta, które dzielą jego obwód na dwie części, z których każda zawiera taką samą liczbę odcinków długości 2 i taką samą liczbę odcinków długości 3.
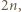 a jego wierzchołkami będą kolejno
a jego wierzchołkami będą kolejno 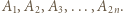 Dla
Dla 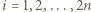 niech
niech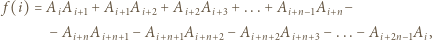
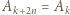 dla
dla 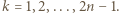 Innymi słowy,
Innymi słowy, 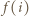 jest różnicą długości części, na które dzielą obwód wielokąta punkty
jest różnicą długości części, na które dzielą obwód wielokąta punkty 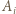 oraz
oraz 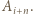 Ponieważ
Ponieważ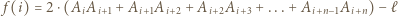
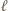 jest obwodem danego wielokąta), to
jest obwodem danego wielokąta), to 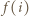 jest liczbą parzystą. Ponadto mamy
jest liczbą parzystą. Ponadto mamy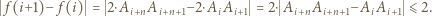
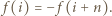 Stąd wynika, że ciąg liczb
Stąd wynika, że ciąg liczb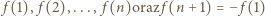
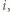 że
że 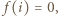 czyli punkty
czyli punkty 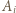 oraz
oraz 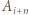 dzielą obwód danego wielokąta na dwie części o jednakowej długości.
dzielą obwód danego wielokąta na dwie części o jednakowej długości.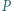 leży wewnątrz trójkąta ostrokątnego
leży wewnątrz trójkąta ostrokątnego 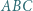 i nie jest środkiem okręgu
i nie jest środkiem okręgu 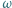 opisanego na tym trójkącie. Udowodnić, że wśród odcinków
opisanego na tym trójkącie. Udowodnić, że wśród odcinków 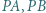 i
i 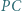 znajdują się odcinek krótszy oraz odcinek dłuższy od promienia okręgu
znajdują się odcinek krótszy oraz odcinek dłuższy od promienia okręgu 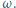
 leży wewnątrz trójkąta
leży wewnątrz trójkąta  i
i 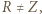 to
to 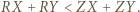 Aby go udowodnić, zauważmy najpierw, że
Aby go udowodnić, zauważmy najpierw, że 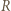 nie leży na co najmniej jednym z odcinków
nie leży na co najmniej jednym z odcinków 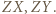 Bez straty ogólności przyjmijmy, że jest to
Bez straty ogólności przyjmijmy, że jest to 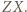 Niech
Niech 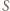 będzie punktem przecięcia prostych
będzie punktem przecięcia prostych 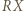 i
i 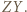 Wtedy z nierówności trójkąta:
Wtedy z nierówności trójkąta: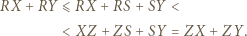
 będzie środkiem okręgu
będzie środkiem okręgu  a
a  będzie promieniem tego okręgu. Punkt
będzie promieniem tego okręgu. Punkt  leży w co najmniej jednym z trójkątów
leży w co najmniej jednym z trójkątów 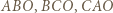 ; bez straty ogólności przyjmijmy, że jest to trójkąt
; bez straty ogólności przyjmijmy, że jest to trójkąt 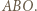 Podobnie,
Podobnie, 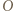 leży w którymś z trójkątów
leży w którymś z trójkątów 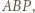
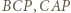 ; przyjmijmy, że jest to trójkąt
; przyjmijmy, że jest to trójkąt 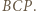 Zgodnie z lematem zachodzi
Zgodnie z lematem zachodzi 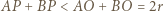 ; i analogicznie:
; i analogicznie: 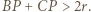 Zatem któryś z odcinków
Zatem któryś z odcinków 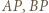 jest mniejszy od
jest mniejszy od  i któryś z odcinków
i któryś z odcinków 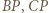 jest większy od
jest większy od 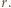
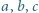 są długościami boków trójkąta, to
są długościami boków trójkąta, to
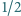 (po prawej stronie) może być zastąpiony przez liczbę większą?
(po prawej stronie) może być zastąpiony przez liczbę większą?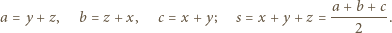
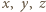 to długości fragmentów boków od wierzchołków do punktów styczności z okręgiem wpisanym. Oznaczając przez
to długości fragmentów boków od wierzchołków do punktów styczności z okręgiem wpisanym. Oznaczając przez 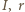 środek i promień okręgu wpisanego, mamy zgodnie z twierdzeniem Pitagorasa
środek i promień okręgu wpisanego, mamy zgodnie z twierdzeniem Pitagorasa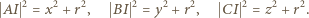
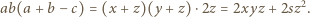
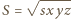 (wzór Herona) oraz
(wzór Herona) oraz 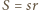 ; stąd
; stąd 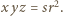 Kontynuujemy przekształcenie (1):
Kontynuujemy przekształcenie (1):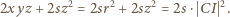
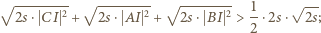
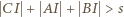
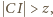
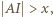
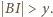
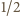 (w oryginalnej nierówności) jest optymalna.
(w oryginalnej nierówności) jest optymalna.