Zadanie ZM-17.11-Deltoid-1
o zadaniu...
- Publikacja w Delcie: listopad 2017
- Publikacja elektroniczna: 31 października 2017
Mamy dwa ziemniaki. Wykaż, że istnieje taka krzywa zamknięta w przestrzeni trójwymiarowej, którą da się narysować na powierzchni każdego z tych ziemniaków.

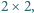 jak na rysunku. Połącz wszystkie te punkty za pomocą łamanej złożonej z czterech odcinków.
jak na rysunku. Połącz wszystkie te punkty za pomocą łamanej złożonej z czterech odcinków.
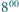 turysta wyruszył z domu u podnóża góry i o
turysta wyruszył z domu u podnóża góry i o 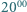 dotarł do schroniska na szczycie. O
dotarł do schroniska na szczycie. O 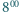 następnego dnia wyruszył ze szczytu tą samą trasą i o
następnego dnia wyruszył ze szczytu tą samą trasą i o 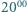 wrócił do domu. Udowodnij, że istnieje taki punkt, w którym turysta był w oba dni dokładnie o tej samej godzinie.
wrócił do domu. Udowodnij, że istnieje taki punkt, w którym turysta był w oba dni dokładnie o tej samej godzinie.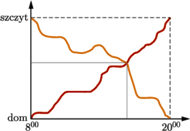
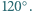 Czy łamana ta musi być sześciokątem foremnym?
Czy łamana ta musi być sześciokątem foremnym?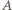 i
i 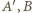 i
i 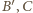 i
i 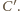 Łamana
Łamana 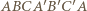 spełnia warunki zadania. Odpowiednie odcinki są równe, bo ośmiościan jest foremny i równoległe, bo
spełnia warunki zadania. Odpowiednie odcinki są równe, bo ośmiościan jest foremny i równoległe, bo 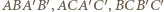 są kwadratami. Ściany tego ośmiościanu są trójkątami równobocznymi, więc wszystkie pary kolejnych prostych tworzą kąty
są kwadratami. Ściany tego ośmiościanu są trójkątami równobocznymi, więc wszystkie pary kolejnych prostych tworzą kąty 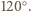
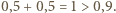 Istnieje więc taka płaszczyzna przechodząca przez środek, że cała elipsoida jest po jednej jej stronie. Wtedy po drugiej stronie otrzymujemy nietkniętą przez robaczka połówkę jabłka.
Istnieje więc taka płaszczyzna przechodząca przez środek, że cała elipsoida jest po jednej jej stronie. Wtedy po drugiej stronie otrzymujemy nietkniętą przez robaczka połówkę jabłka. i stałej
i stałej 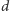 to zbiór takich punktów
to zbiór takich punktów 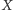 przestrzeni, dla których
przestrzeni, dla których 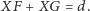 Punkty
Punkty 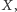 dla których
dla których 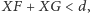 tworzą wnętrze elipsoidy. Elipsoida jest figurą wypukłą.
tworzą wnętrze elipsoidy. Elipsoida jest figurą wypukłą.
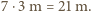 Stąd na mocy twierdzenia Pitagorasa długość winorośli to 29 m.
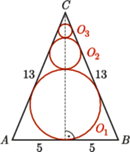
Stąd na mocy twierdzenia Pitagorasa długość winorośli to 29 m. jest wpisany w trójkąt
jest wpisany w trójkąt 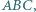 w którym
w którym 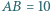 i
i 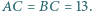 Okręgi
Okręgi 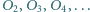 są styczne do boków
są styczne do boków 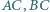 oraz dla każdego
oraz dla każdego 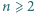 okrąg
okrąg 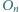 jest styczny zewnętrznie do okręgów
jest styczny zewnętrznie do okręgów 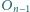 i
i 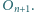 Wyznacz sumę obwodów wszystkich okręgów
Wyznacz sumę obwodów wszystkich okręgów 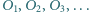
 która z kolei z twierdzenia Pitagorasa ma długość 12. Okrąg o średnicy
która z kolei z twierdzenia Pitagorasa ma długość 12. Okrąg o średnicy 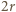 ma obwód
ma obwód 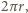 zatem szukana suma obwodów wszystkich okręgów to
zatem szukana suma obwodów wszystkich okręgów to 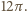
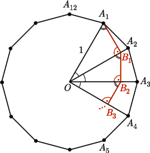
 o środku
o środku 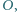 przy czym
przy czym 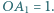 Punkt
Punkt 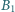 jest rzutem
jest rzutem 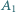 na odcinek
na odcinek 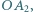 punkt
punkt 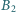 jest rzutem
jest rzutem 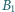 na
na 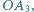 punkt
punkt 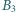 jest rzutem
jest rzutem 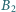 na
na 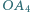 itd. Wyznacz długość łamanej
itd. Wyznacz długość łamanej 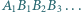

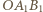 oraz
oraz 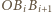 mają kąty po
mają kąty po 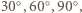 gdyż każdy z nich z założenia jest prostokątny i ma kąt
gdyż każdy z nich z założenia jest prostokątny i ma kąt 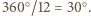 Można wobec tego ułożyć je w sposób przedstawiony na rysunku. Kąt pomiędzy sąsiadującymi teraz odcinkami rozważanej łamanej jest wówczas równy
Można wobec tego ułożyć je w sposób przedstawiony na rysunku. Kąt pomiędzy sąsiadującymi teraz odcinkami rozważanej łamanej jest wówczas równy 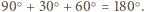
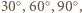 przy czym jedna jego przyprostokątna ma długość 1, a suma pozostałych dwóch boków to szukana długość łamanej. Jest ona wobec tego równa
przy czym jedna jego przyprostokątna ma długość 1, a suma pozostałych dwóch boków to szukana długość łamanej. Jest ona wobec tego równa 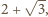 gdyż trójkąt ten jest połową trójkąta równobocznego o boku 2.
gdyż trójkąt ten jest połową trójkąta równobocznego o boku 2.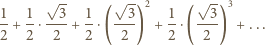
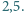 Wykaż, że obwód tego czworokąta jest większy od 7.
Wykaż, że obwód tego czworokąta jest większy od 7.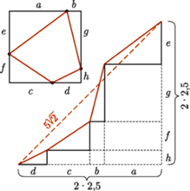
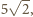 co z kolei jest większe od 7.
co z kolei jest większe od 7.