Delta mi!

W salonie fryzjerskim siedzi matematyk, obok leży połyskująca para nożyczek, mnóstwo szczotek i innych sprzętów. Matematyk nerwowo wierci się w fotelu - przecież nie od dziś wie, że sfery zaczesać się nie da. Fryzjer intuicyjnie sięga po nożyczki, szalejące nad czołem rozmaitości nie rokują zbyt dobrze. Niechętny rozspójnieniu klient wpada na pomysł - warkocz będzie idealny!

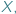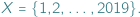Ustalmy zbiór np. Niech 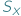oznacza zbiór funkcji odwracalnych z 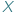w Funkcje z 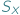można składać i odwracać, nie wychodząc poza 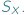W zbiorze 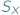istnieje też funkcja identycznościowa. Tytułowe grupy są abstrakcyjnym sposobem wyrażenia powyższych własności zbioru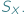

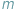W 1967 roku szkoła podstawowa wypuściła po raz pierwszy absolwentów ośmioletniej podstawówki (tak, kiedyś też były reformy szkolne). W ogólnym reformatorskim zamieszaniu można było zrobić coś nietypowego, więc Wydział Matematyki i Fizyki Uniwersytetu Warszawskiego uruchomił uniwersyteckie klasy matematyczno-fizyczne w liceum im. Klementa Gottwalda (w latach 1906-50 oraz po 1990 roku Stanisława Staszica) - pretekst był prosty: pierwszym dyrektorem tego liceum był Jan Zydler, znakomity nauczyciel matematyki i autor do dziś niezapomnianych podręczników geometrii.

Ten artykuł będzie poświęcony zliczaniu różnych kolorowań obiektów, które podlegają symetrii. Wyobraźmy sobie, że Kalina chciałaby pokolorować rogi kwadratu za pomocą kolorów. Ile różnych figur może w ten sposób otrzymać?

Grupa warkoczy była rozważana po raz pierwszy przez Adolfa Hurwitza w roku 1885, jednak nie pod tą nazwą; w grupie rozważanej przez Hurwitza trudno było dopatrzyć się warkoczy. Nazwę wprowadził Emil Artin w roku 1925, bo w jego interpretacji elementy grupy kojarzą się z warkoczami. Przypomnę, jak się je zaplata...

Dla mnie odpowiedź nie jest oczywista. W pierwszej chwili pomyślałem, że nie jest potrzebna, ale to było sprowokowane samym pytaniem.

Słowa, którymi będziemy się zajmowali, będą napisami złożonymi z liter jednego lub kilku zbiorów (na początek przyjmijmy, że zbiory są dwa – jeden zawiera małe litery łacińskie, a drugi duże) o tej własności, że dwie jednakowe litery umieszczone po kolei będą znikały. Napis, w którym wszystko znikło (czasem i taki jest potrzebny), będzie oznaczany 1.

30 maja 1832 roku w Paryżu zginął w pojedynku młody matematyk, Evariste Galois. Nie ma pewności, czy pojedynek ten miał podłoże polityczne, czy też Galois bronił honoru pewnej młodej damy. W pożegnalnym liście poprosił on, by jego notatki wysłać Jacobiemu albo Gaussowi. Żaden z tych wielkich matematyków nigdy nie zobaczył jednak zapisków Galois.

Spójrzmy na cztery z pozoru zupełnie niezwiązane zadania...

Płaszczyznę można wyposażyć w działania dodawania i mnożenia jej punktów. Dlaczego nie można tego zrobić z przestrzenią ?

Na ile sposobów można przykryć banknotem prostokąt o tych samych rozmiarach? xxx Każdy od razu zgadnie, że na cztery sposoby: do góry orłem, przy czym orzeł może być do dołu lub do góry nogami, i podobnie na dwa sposoby królem do góry (choć na banknocie nie widać jego nóg).