Delta mi!

W dowolnym trójkącie odcinek łączący środki dwóch boków jest równoległy do trzeciego boku i dwukrotnie od niego krótszy. Ten prosty fakt okazuje się zadziwiająco przydatny.

Tym razem będziemy wycinać...

Twierdzenie Talesa dowieść można bez trudu...

Panuje przekonanie, że w niemodnej obecnie dziedzinie geometrii klasycznej wszystko jest znane i nie pozostało nic do odkrycia. Kłam temu stwierdzeniu zadaje dość ciekawe i (jeszcze) mało znane twierdzenie, które przedstawiamy w niniejszym artykule. Warto zaznaczyć, że środki, jakie posłużyły nam do dowodu, są czysto geometryczne i nie korzystają z narzędzi analitycznych. Aby ułatwić jego zrozumienie, przedstawiamy najpierw pewne pojęcia, definicje i bardziej znane fakty powiązane z tym zagadnieniem.

W niniejszym artykule przybliżymy własności jednej z najsłynniejszych prostych w geometrii euklidesowej - prostej Simsona. Jej odkrycie przypisywane jest szkockiemu matematykowi, Robertowi Simsonowi, choć w żadnej jego pracy nie znajdujemy wzmianki o niej.

Gwiazdka foremna to łamana zamknięta, wpisana w okrąg i złożona z jednakowej długości cięciw, ale niebędąca wielokątem foremnym. Nie trzeba długo się zastanawiać, by stwierdzić, że odcinki takich łamanych muszą się przecinać.

Na pierwszym etapie XI Olimpiady Matematycznej Gimnazjalistów pojawiło się pytanie, na które tylko 24% uczestników odpowiedziało poprawnie...

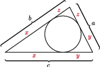
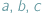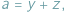
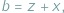
Jeśli w nierówności, którą chcemy uzasadnić, występują długości boków pewnego trójkąta, często przydaje się podstawienie Raviego: 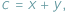gdzie 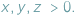Takie liczby 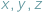zawsze istnieją, są to bowiem długości odcinków stycznych do okręgu wpisanego w trójkąt.

Euklides w Elementach pisał: "... kwadrat jest tym, co równoboczne i prostokątne...". Oto kilka niebanalnych obserwacji, w których kwadrat jest jednym z bohaterów.

W artykule tym pragnę omówić pewne pojęcia, należące całkowicie do zakresu geometrii elementarnej, a dotąd niemal wcale nie zbadane. Jak wiadomo, dwa wielokąty 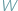i 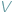nazywamy równoważnymi, wyrażając to wzorem: 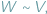jezeli dają się one podzielić na jednakową ilość wielokątów odpowiednio przystających...

Rozpatrzmy dowolny trójkąt oraz cztery kwadraty zbudowane w sposób przedstawiony na rysunku 1. Wówczas zaznaczone kolorem trzy odcinki, łączące odpowiednie wierzchołki kwadratów oraz środek najniższego kwadratu, przecinają się w jednym punkcie.

...a pięciokąt foremny można. Obok pokazana jest konstrukcja dziesięciokąta foremnego - kolorowy odcinek ma długość boku dziesięciokąta foremnego wpisanego w większy okrąg, a więc biorąc co drugi z wierzchołków takiego dziesięciokąta, otrzymamy pięciokąt foremny. Konstrukcja jest - jak widać - bardzo prosta. Ma tylko tę wadę, że nie wskazuje, jak konstruować inne wielokąty foremne.

Z twierdzeniem Pitagorasa wszyscy się znamy, budowanie kwadratów na bokach trójkąta prostokątnego nie jest niczym nadzwyczajnym. A co możemy powiedzieć ciekawego o prostokątach skonstruowanych na bokach dowolnego trójkąta?

W LXVI Olimpiadzie Matematycznej uczestniczyło 895 uczniów, więc aż o 272 osoby mniej niż rok wcześniej, do zawodów stopnia drugiego zakwalifikowano 409 uczniów, a do zawodów stopnia trzeciego -126 uczniów. Wiele osób, w tym niżej podpisany, uznało, że zadania domowe były za trudne i nie zachęcały uczniów spoza szkół o dużych tradycjach olimpijskich (a raczej uczniów nauczycieli, którzy uczą matematyki, a nie tylko przygotowują do zdania matury) do startowania w tych zawodach.

W każdym zjawisku przyrody można dostrzec dążenie do osiągnięcia jakiegoś maksimum lub minimum. Umiejętność wyznaczania wartości ekstremalnych nie powinna więc być niczym niezwykłym...

Zechciejcie państwo wysłuchać dziś krótkiej opowieści z królestwa geometrii. Za siedmioma górami matematycznych podręczników, za siedmioma rzekami matematycznych równań, za siedmioma lasami matematycznych sprzeczności znajdowała się symediana. Dziś symediana ujrzy światło dzienne...

Zająłem się ciekawym problemem dotyczącym centrów trójkąta. Ciekawym, bo łatwym do wyobrażenia, a w pewnych aspektach nawet bardzo trudnym.

Niektórzy sądzą, że geometria jest trudna. Oto zadanie, które wielu by odstraszyło...