
Rys. 1
Odkryj wielokąt!
Punkty z rysunku obok, jako środki kolejnych boków wielokąta, kodują pewien obrazek. Czy potrafisz go odtworzyć? Spróbuj!

Rys. 1
Punkty z rysunku obok, jako środki kolejnych boków wielokąta, kodują pewien obrazek. Czy potrafisz go odtworzyć? Spróbuj!
Planimetria Kącik początkującego olimpijczyka
O prostej Eulera i okręgu dziewięciu punktów.
Planimetria Kącik początkującego olimpijczyka
Najbardziej królewskie części trójkąta i ich własności.
Tytułowe twierdzenie sformułujemy dla trójkąta (z brzegiem) na płaszczyźnie euklidesowej 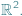 Jest to najsłynniejsze i najważniejsze twierdzenie w topologicznej teorii punktów stałych o rozlicznych zastosowaniach (w równaniach różniczkowych, topologii, ekonomii, teorii gier, analizie funkcjonalnej). Jego odkrycie miało ogromny wpływ na rozwój wielu gałęzi matematyki, szczególnie topologii algebraicznej.
Jest to najsłynniejsze i najważniejsze twierdzenie w topologicznej teorii punktów stałych o rozlicznych zastosowaniach (w równaniach różniczkowych, topologii, ekonomii, teorii gier, analizie funkcjonalnej). Jego odkrycie miało ogromny wpływ na rozwój wielu gałęzi matematyki, szczególnie topologii algebraicznej.
Planimetria Kącik początkującego olimpijczyka
O znajdowaniu i dorysowywaniu równoległoboków oraz stosowaniu ich własności.
Planimetria Kącik początkującego olimpijczyka
Przedstawiamy wygodne narzędzie geometryczne o wielu zastosowaniach, wśród których znajduje się dowodzenie współliniowości punktów.
Planimetria Kącik początkującego olimpijczyka
Gdy w zadaniu występuje kąt o mierze będącej wielokrotnością 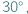 to jest spora szansa na to, że gdzieś tam jest ukryty trójkąt równoboczny.
to jest spora szansa na to, że gdzieś tam jest ukryty trójkąt równoboczny.
Matematyka Kącik początkującego olimpijczyka
O paru zasadach pozwalających stwierdzić, który z dwóch zbiorów ma więcej elementów, ale bez liczenia elementów tych zbiorów.

Niniejszy odcinek Deltoidu o okrągłym (w systemie jedenastkowym) numerze jest odcinkiem ostatnim. Nie kryjemy smutku z tego powodu, cieszymy się jednocześnie, że na naszych łamach ta wspaniała seria ukazywała się przez okrągłych 10 lat. Mamy nadzieję, że jeszcze wiele razy nazwisko Autorki zagości w naszym spisie treści.
Joasiu, za Twoją nienaganną punktualność w dostarczaniu materiałów, zegarmistrzowską dokładność przy ich korekcie, a przede wszystkim za deltoidową fantastyczność serdecznie dziękujemy!
Redakcja

Rys. 1
W Delcie 11/2017 został przedstawiony (bez dowodu) fakt, że dla czterech dowolnych prostych (tak dowolnych, że są parami nierównoległe i żadne trzy nie mają punktu wspólnego) ortocentra wyznaczonych przez nie czterech trójkątów leżą na jednej prostej, a okręgi opisane na tych trójkątach mają punkt wspólny. Ponadto parabola, której kierownicą jest prosta zawierająca ortocentra, a ogniskiem punkt wspólny okręgów opisanych jest styczna do czterech wyjściowych prostych (Rys. 1).
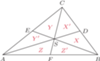
Punkty D, E, F to środki boków, X, X', Y, Y', Z, Z' oznaczają pola.
Środkowa trójkąta to odcinek łączący wierzchołek ze środkiem przeciwległego boku. Środkowe przecinają się w jednym punkcie, zwanym środkiem ciężkości i dzieli on każdą z nich w stosunku 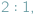 licząc od wierzchołka trójkąta (rys. obok).
licząc od wierzchołka trójkąta (rys. obok).
Wysokością czworokąta nazwijmy prostą przechodzącą przez środek jego boku i prostopadłą do boku przeciwległego. W niektórych czworokątach wszystkie cztery wysokości przecinają się w jednym punkcie - ortocentrum czworokąta. Przykładowo kwadrat ma ortocentrum, a romb niebędący kwadratem nie ma.
W wielu zadaniach, w których występują kąty lub ich sumy, przydatne bywa przeniesienie pewnych figur tak, by kąty te znalazły się obok siebie. Szczególnie wygodne jest to wtedy, gdy suma pewnych kątów równa jest np. 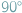 lub
lub 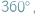 a także, gdy niektóre z danych odcinków są równej długości.
a także, gdy niektóre z danych odcinków są równej długości.
W tym artykule omówimy pewną bardzo pożyteczną technikę - tzw. przesuwanie. Polega ona na tym, że niektóre obiekty przesuwamy o pewien wektor i udowadniamy, że teza zadania jest niezmiennicza ze względu na wykonanie tej operacji. Ta metoda pozwala na sprowadzenie rozwiązywanego zadania do znacznie prostszego. Bardzo często ten prostszy przypadek ma jakiś rodzaj symetrii, z której łatwo wywnioskować tezę. Zanim przejdziemy do rozwiązywania zadań, odnotujmy dwie proste własności opisanej operacji.
Proste do zdefiniowania i zrozumienia problemy geometryczne często są trudne do rozwiązania i wymagają użycia skomplikowanych algorytmów. Weźmy, na przykład, zadanie polegające na znalezieniu największego okręgu, który możemy zmieścić w wielokącie. Środek tego okręgu nazywany jest środkiem Czebyszewa. Jeżeli mamy do czynienia z dowolnie wybranym trójkątem bądź wielokątem foremnym, środek Czebyszewa znajduje się w punkcie przecięcia dwusiecznych jego dwóch dowolnych kątów. Zagadnienie staje się o wiele bardziej skomplikowane, gdy weźmiemy pod uwagę dowolny, nieregularny wielokąt.
Tzw. zagadnienie Fermata to pytanie o to, gdzie wewnątrz danego trójkąta 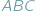 należy umieścić punkt
należy umieścić punkt  aby suma długości odcinków
aby suma długości odcinków 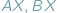 i
i 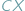 przyjęła najmniejszą wartość.
przyjęła najmniejszą wartość.
W geometrii dyskretnej przyjęło się mówić, że wielokąt jest wpisany w inny wielokąt, gdy ma wierzchołki na prostych zawierających boki tego drugiego wielokąta. Od czasu Hilberta tego zwrotu używa się i w przypadku "zwyczajnej" geometrii.
...z których żadne dwie nie są równoległe, a żadne trzy nie mają punktu wspólnego... tworzą cztery trójkąty - to każdy widzi i nikt się nie dziwi.

Rys. 1
Odcinek 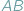 widać z punktu
widać z punktu 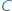 pod kątem
pod kątem 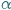 , gdy
, gdy 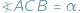 Z twierdzenia o kątach wpisanych wynika, że jeśli punkty
Z twierdzenia o kątach wpisanych wynika, że jeśli punkty 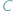 i
i 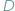 leżą na okręgu po tej samej stronie jego cięciwy
leżą na okręgu po tej samej stronie jego cięciwy 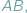 to widać ją z
to widać ją z 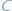 i
i 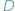 pod tym samym kątem (Rys. 1).
pod tym samym kątem (Rys. 1).

Fakt (*). W trójkącie prostokątnym środek przeciwprostokątnej jest równo odległy od wierzchołków. Również na odwrót, jeśli środek okręgu opisanego leży na boku trójkąta, to trójkąt ten jest prostokątny.