Delta mi!

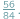
- Z tymi ułamkami to zupełnie nic nie wiadomo - narzekał po lekcji matematyki Janek. - Na przyklad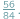

Kiedy Zbyszek miał siedem lat, pojechał po raz pierwszy na kolonie. Mieszkał tam wraz z innymi chłopcami, w dużej sali, do której przylegała mała komórka bez okien. Pewnego razu, bawiąc się w chowanego, ukrył się Zbyszek w komórce. Było tam oczywiście ciemno, jedyne światło dochodziło z sali przez dziurkę od klucza...

Taka sobie niewinnie wyglądająca bryłka. Ot, powstała z obrotu kwadratu dookoła jego przekątnej, przecięcia tego, co powstało, na dwie identyczne części (wzdłuż płaszczyzny kwadratu), przekręceniu połowy o 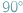i doklejeniu do drugiej części (czekającej w tym czasie w bezruchu). Szczęśliwa całość - sferostożek (ang. sphericon).

Dym zaczął radośnie buchać ze starego, ceglanego komina. To znak, że Czerwony Kapturek, właścicielka najbardziej czerwonego kubraczka w stumilowym lesie, rozpoczęła już swoje wyśmienite wypieki. Świeżutkie bułeczki dostaną wszyscy ci i tylko ci mieszkańcy lasu, którzy sami nie robią dziś wypieków...

Jaką długość ma linia śrubowa owijająca dwukrotnie walec o promieniu 1 i wysokości 4, tak jak widać na obrazku? Oczywiście, 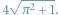Aby przekonać się, że rzeczywiście, wystarczy spojrzeć na obrazek z prawej - jeśli nawiniemy go na walec, to otrzymamy obrazek z lewej.

Dawno, dawno temu za górami, za lasami na Euklidesowych Równinach żyło sobie koło. Niezmiernie było dumne ze swej stałej szerokości. Chadzało ścieżkami, które miały szerokość równą jego średnicy, i jako jedyna figura zamieszkująca równiny mogło kręcić się przy tym jak szalone, stale podpierając obie krawędzie ścieżki.

W pewnym mieście podjęto decyzję o budowie nowego osiedla. Postanowiono, że będzie to szereg ośmiu budynków. Przyjęto, że żadne trzy stojące obok siebie budynki nie mogą być tej samej wysokości. Ustalono, że budynki będą mieć wysokości równe odpowiednio: 5, 10, 10, 15, 25, 25, 30 i 45 metrów...

Niektórzy znajdują co rano na progu swojego domu butelkę ze świeżym mlekiem. Kubuś Puchatek każdego ranka znajduje tam 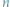garnczków miodu. Garnczki są różnej wielkości i Kubuś każdego dnia stara się opróżniać je w innej kolejności...

Bryła to stworzenie, z którym większość z nas poznała się w szkole podstawowej i które było przez nas oswajane przez kolejne lata edukacji. Znamy bliżej różne rodziny brył, takie jak wielościany, graniastosłupy, bryły obrotowe, foremne, platońskie. Oczywiście, można produkować nowe stworzenia, łącząc czy tnąc "podstawowe" gatunki, a jedynym ograniczeniem jest nasza wyobraźnia.

Król Chimeryk zaniemógł. Wezwał do swojego łoża trzech synów. „Czas mój się wypełnia, bo choroba moja straszna i lekarstwa na nią nie znam. Jedna jeszcze nadzieja została. Za siedmioma górami i siedmioma lasami mieszka stary pustelnik, który ma wiedzę wielką o wszelakich chorobach i sam rozmaite medykamenty przygotowuje sobie tylko znanymi sposobami. Synowie moi! W waszych rękach moje życie i ostatnia nadzieja na jego przedłużenie.”

Jednym z najbardziej charakterystycznych elementów architektury średniowiecznej, zwłaszcza gotyckiej, są rozety. Są to okrągłe okna z delikatną konstrukcją kamienną, których puste przestrzenie są najczęściej wypełnione witrażami. Pierwsze rozety pojawiają się już w kościołach romańskich; zamiast witrażami są wypełnione cienkimi płytkami kamiennymi, przepuszczającymi światło.

Kto by się spodziewał, że prawdziwe jest stwierdzenie: jeśli w sześcianie mieszczą się trzy jednakowe kulki, to zmieści się też czwarta tej samej wielkości!

Wyobraźmy sobie, że trafiliśmy do dziwnego kraju, w którym jedynymi dostępnymi środkami płatniczymi są monety o nominałach 5 i 9. Formy płatności nie rozwinęły się na tyle, żeby płacić kartą lub czekiem, na domiar złego wybraliśmy się do cukierni, w której kasa jest zupełnie pusta i sprzedawca nie może wydać nam reszty...

...jeśli ma się 5 jego punktów. No, może trochę przesadziłem... Okręgu tak dosłownie nakreślić nie można, ale można narysować jego kolejnych kilka punktów, nawet gdy te kilka to np. 100 -- oczywiście, im większa będzie to liczba, tym dłużej będzie to trwało, bo rysować będziemy te punkty kolejno, po jednym.

Żyjemy w czasach, w których poznawanie Wszechświata przez obserwacje, czyli zwykłe oglądanie nieba, staje się coraz trudniejsze. To dość zaskakujące, bo przecież amatorski sprzęt astronomiczny jest względnie łatwo dostępny. Problemem jest jednak „zanieczyszczenie światłem”, które szczególnie w miastach rozjaśnia nocne niebo, uniemożliwiając nawet proste amatorskie obserwacje. Zatem, jeśli mieszkasz w mieście i chcesz zobaczyć prawdziwą czerń kosmicznych przestworzy, wybierz się do... lasu.

Od najmłodszych lat każdy z nas poznaje świat liczb, zliczając zabawki, jabłka czy książki. Nikogo nie dziwi zatem przedstawienie liczby 5 jako pięciu kulek. Tylko czy takie przedstawienie może pomóc w odkrywaniu świata komuś, kto ukończył już przedszkole? Okazuje się, że tak – wystarczy uważne spojrzenie i wyobraźnia, a może nam przynieść nieoczekiwane spostrzeżenia.

Dwunastościan wielki jest jednym z czterech niewypukłych wielościanów foremnych. Jego ścianami są przenikające się pięciokąty foremne (pentagony). Oczywiście, jest ich dwanaście. I w tym przypadku jest w miarę prosty sposób rysowania.

Dwunastościan rombowy jest figurą o zadziwiających własnościach. Narysowanie go nie powinno sprawiać większych trudności. Jak nazwa wskazuje, ścianami tego dwunastościanu są romby, zatem rysunek zaczynamy od narysowania właśnie rombu.

Któż nie chciałby być jak pilot Pirx? Osadzona w bliskiej przyszłości (XXI, XXII wiek?) opowieść w stylu retro o przygodach pilota statków międzyplanetarnych rozwija wyobraźnię kolejnego pokolenia. Szczególnie interesujący jest opis technologii, z której korzysta Pirx...

Ostatnio rysowaliśmy dwunastościan foremny i dwudziestościan foremny. Przedstawimy jeszcze jeden sposób rysowania dwunastościanu foremnego.

Jeffrey spojrzał w kierunku piekarnika, gdzie apetycznie brązowiało kruche ciasto nadziewane jabłkami. Był pewien, że odkrył naukową metodę umożliwiającą otrzymanie ciasta idealnego: o strukturze cieniutkich płatków, delikatnego, ale chrupkiego.

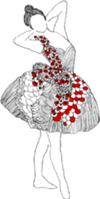
Co fizycy robią „po godzinach”? Różnorodność odpowiedzi na to pytanie jest pewnie taka jak w innych grupach zawodowych. Naukowcy mogą jednak mówić o swoich pasjach, używając języka „pracowego”. Tak właśnie powstał wykład poświęcony fizyce tańca, którym włączyłam się w cykl imprez Festiwalu Nauki i którego kilka urywków chciałabym Czytelnikom Delty przedstawić.

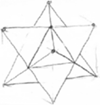
Narysujemy teraz figurę bardziej skomplikowaną: dwudziestościan...

Do dzisiejszego doświadczenia potrzebna będzie huśtawka. Jeszcze lepszy byłby długi, spuszczony z gałęzi sznur z poprzeczką na końcu. Każdy chyba umie rozhuśtać się. Ale czy zastanawialiście się kiedyś, dlaczego to jest możliwe i dlaczego wszyscy robią to w prawie identyczny sposób? Może jest to spowodowane naśladownictwem?

Legenda powiada, że gdy bóg Brahma po raz pierwszy poruszył czas, umieścił na jednej z trzech diamentowych igieł, umocowanych na wspólnej podstawce, 64 złote krążki. Na podstawce spoczywał krążek najszerszy, a nad nim lśniły pozostałe o coraz mniejszych średnicach. Bóg polecił mnichom z górskiej samotni, by bez spoczynku przekładali krążki, tak aby wszystkie znalazły się na drugiej diamentowej igle, z zachowaniem tego samego ułożenia. Gdy zadanie zostanie zakończone, nastąpi koniec pierwszego świata, a na następny, wskrzeszony przez Brahmę, wypadnie czekać wiele tysięcy lat...

Wyobraźmy sobie następującą grę. Na stole w jednym rzędzie leży  monet o różnych nominałach. Dwoje graczy – Ania i Bartek – wykonuje na przemian ruchy, zaczyna Ania. Ruch polega na zabraniu jednej monety z lewego lub prawego końca rzędu. Wynikiem gry jest, oczywiście, suma nominałów monet zgromadzonych przez każdego z graczy. Jak powinna grać Ania, by uzyskać jak największą sumę, jeśli wie ona, że Bartek będzie grał optymalnie (tzn. będzie starał się zmaksymalizować swoją sumę)?

W wielu rysunkach bardzo pomocny jest sześcian, z narysowaniem którego raczej nie mamy problemu...

Wielką przyjemność i satysfakcję sprawia obserwowanie przyrody. Nieporównanie większą – obserwowanie jej z poczuciem zrozumienia. Jednak największą odczuwa się chyba w trakcie samodzielnego jej poznawania. Jak wielką satysfakcję może sprawić wyznaczenie odległości do Wenus? Nie dowiesz się, jeśli nie spróbujesz tego dokonać. A warto, bo doświadczysz nie tylko satysfakcji badawczej...

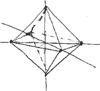
Kontynuujemy lekcje rysunku rozpoczęte w Delcie 6/2012. Kolejnym obiektem, który będziemy rysować, jest ośmiościan.

W dniu naszego powrotu z Grenoble, gdzie przez dwa tygodnie pomagaliśmy miejscowej policji uporać się z problemem – z pozoru błahym, lecz o jakże przygnębiającym rozwiązaniu – znikających przydrożnych lamp gazowych, w mieszkaniu przy Baker Street 221B oczekiwał niezaniedbywalnej wielkości stos korespondencji...

Wydaje się, że w czasach szybkich komputerów, programów graficznych i innych gadżetów nie ma sensu zajmowanie się rysunkiem odręcznym. Równie dobrze jednak można by zrezygnować z nauki pisania i tabliczki mnożenia – są przecież odpowiednie edytory i kalkulatory. Zdarza się jednak, że rozwiązując jakieś zadanie, dobrze byłoby podeprzeć naszą wyobraźnię właśnie rysunkiem, a nie ma pod ręką supernowoczesnych narzędzi.

Co to jest liczba pierwsza? Najkrótsza definicja mówi, że to taka liczba naturalna, która ma dokładnie dwa dzielniki. Każda liczba naturalna ma przynajmniej dwa dzielniki: 1 i samą siebie. Wyjątkiem jest jedynka, dla której te dwa dzielniki okazują się tym samym.

Czasem przydaje się do czegoś twierdzenie o dwusiecznej...

Girard DESARGUES, matematyk, architekt ogrodów, doradca kardynała Richelieu (a więc rówieśnik Atosa, Portosa i Aramisa) postawił kolegom ogrodnikom pytanie: Jak posadzić 10 drzew w dziesięciu rzędach po 3 drzewa w każdym rzędzie?

Fleksagony to rodzina figur, które odpowiednio złożone z płaskiej kartki papieru mogą wskutek obracania pokazać nam cztery lub więcej „twarzy” (zamiast dwóch).

Każdy od czasu do czasu potrzebuje metody przekazania komuś pewnych wiadomości tak, żeby niepowołane osoby nie miały szans na ich przechwycenie. Począwszy od zabaw z kolegami na podwórku, a skończywszy na operacjach bankowych, wojskowych czy wykorzystujących dane osobowe – bez szyfrów po prostu nie da się żyć. Do zaszyfrowania danych zwykle potrzebny jest klucz – pewne słowo czy liczba, które najpierw kierują procesem tworzenia szyfru, a później pozwalają odbiorcy wiadomości ją odkodować. Osoby, które chcą porozumiewać się za pomocą szyfru, muszą najpierw uzgodnić klucz między sobą. I tu pojawia się problem: jak ustalić klucz, tak żeby nikt oprócz nas nie mógł go poznać?

Trzy kółeczka łatwo ułożyć w trójkąt foremny (czyli równoboczny), cztery w czworokąt foremny (czyli kwadrat), pięć w pięciokąt foremny itd. Można więc 3 uważać za liczbę trójkątną, cztery za czworokątną, pięć za pięciokątną itd. Rysunki poniżej pokazują, jak można, rysując kropki, określić inne liczby wielokątne.

Zróbmy razem kilka doświadczeń myślowych z użyciem kwadratowej kartki papieru i nożyczek. Doświadczenia będą bardzo proste, ale ich wynik – wycinanki (bo cóż by innego) – będą całkiem zaskakujące.

W pewnym kraju żyło bardzo wielu mędrców. Któregoś dnia groźny król postanowił przekonać się, czy rzeczywiście zasługują oni na to zaszczytne miano i zapowiedział, że czeka ich trudna próba. Zebrał mędrców w swej komnacie i przedstawił im poniższe zasady.

Jeszcze dwadzieścia lat temu nie znaliśmy żadnych planet pozasłonecznych. Dzisiejsza technika pozwala nam nie tylko stwierdzić ich istnienie, ale także poznać bliżej ich naturę. Do tej pory naukowcy odkryli niemal pół tysiąca egzoplanet (taką nazwę nadano wszystkim planetom poza Układem Słonecznym).

Oglądając szpargały, jakie w sposób nieunikniony gromadzą się w redakcyjnych szufladach, znalazłem plan lekcji wydany przez Deltę latem 1982 roku – kartonik, format B4.

Ten legendarny koszykarz NBA miał przydomek flying, czyli „latający”. Bardzo często, atakując, wyskakiwał w górę, po nim – na tę samą wysokość – wyskakiwali często wyżsi obrońcy, on jednak potrafił poczekać aż opadną i dopiero wtedy, bez problemu, trafiał do kosza.

Oczywiście chodzi o rekord w skoku wzwyż. Czy można, bez pomocy jakichkolwiek przyrządów, pokonać poprzeczkę zawieszoną na wysokości 2,5 m?

Naprawdę istnieje niewiele gier takich jak szyki, których piękno polega na prostocie, niewielkiej liczby reguł i koniecznych rekwizytów, i jasnym celu gry, które łączą się z wielką złożonością i głębią koniecznych do gry strategii.

W Bajtocji można spotkać wędrownych treserów pcheł. Pchły uczone są tańca, polegającego na wykonywaniu precyzyjnych skoków w rytm muzyki. Dokładnie wygląda to tak: treser układa na stole w rządku ponumerowane kolejno żetony. Na każdym żetonie, oprócz jego numeru, jest również napisany numer żetonu, na który powinna z niego skoczyć pchła – na każdym żetonie ten numer jest inny. Następnie treser ustawia po jednej pchle na każdym z żetonów i włącza muzykę. Na początku każdego taktu każda z pcheł wykonuje skok wprost na żeton, którego numer jest napisany na żetonie, na którym w danej chwili stoi.