NASA (wikipedia)
Wenus
Wycieczka na Wenus
Zaraz po Słońcu i Księżycu Wenus jest najjaśniejszym obiektem widzianym na niebie. Oglądana nocą, przez wielu ludzi traktowana jest omyłkowo jako bardzo jasna gwiazda. Okrąża Słońce w odległości 0,723 j.a., więc jest planetą wewnętrzną (znajdującą się bliżej Słońca niż Ziemia). Dlatego z punktu widzenia obserwatora ziemskiego znajduje się ona na niebie w pobliżu Słońca - czasem bliżej, a czasem dalej.

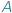 nie jest równoliczny ze zbiorem jego podzbiorów
nie jest równoliczny ze zbiorem jego podzbiorów 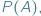 co symbolicznie notujemy
co symbolicznie notujemy 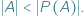 Szczególnie zajmowaliśmy się przypadkiem, gdy
Szczególnie zajmowaliśmy się przypadkiem, gdy 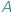 jest zbiorem liczb naturalnych
jest zbiorem liczb naturalnych 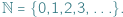
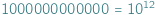 mieści się aż milion milionów, mało kto jest w stanie to sobie wyobrazić. Wszystkie te liczby wpadają w tę samą kategorię - liczb dużych na tyle, że nie znajdujemy dla nich zastosowania w zwyczajnym codziennym życiu.
mieści się aż milion milionów, mało kto jest w stanie to sobie wyobrazić. Wszystkie te liczby wpadają w tę samą kategorię - liczb dużych na tyle, że nie znajdujemy dla nich zastosowania w zwyczajnym codziennym życiu.

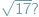 Odpowiedź brzmi: tak.
Odpowiedź brzmi: tak.
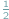 kąta środkowego opartego na tym samym łuku.
kąta środkowego opartego na tym samym łuku.

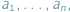 a naszym celem jest znaleźć jego fragment - czyli spójny podciąg - którego suma elementów jest jak największa.
a naszym celem jest znaleźć jego fragment - czyli spójny podciąg - którego suma elementów jest jak największa.